Stratégie de cassure dynamique ajustée à la volatilité de Black-Scholes

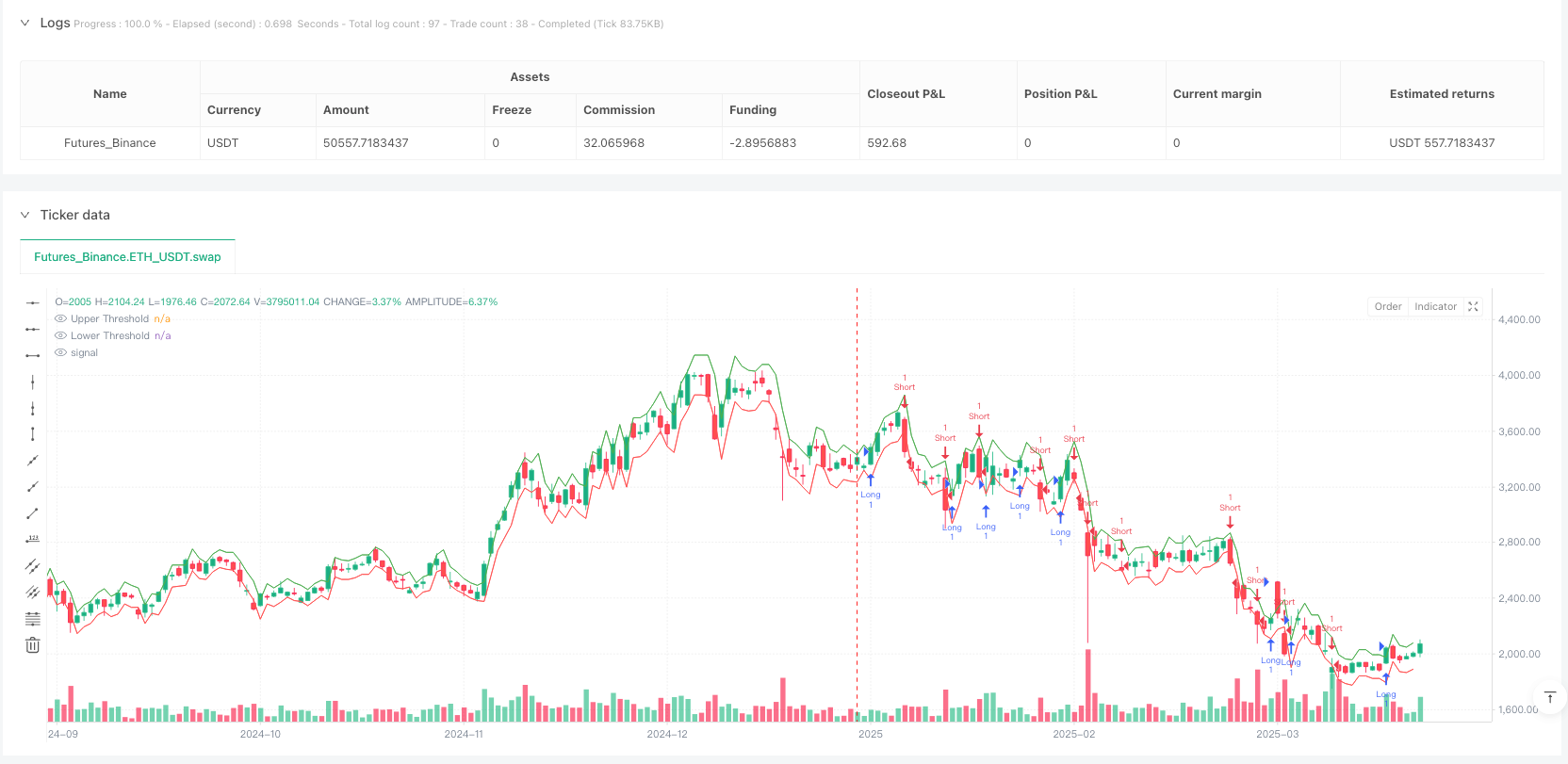
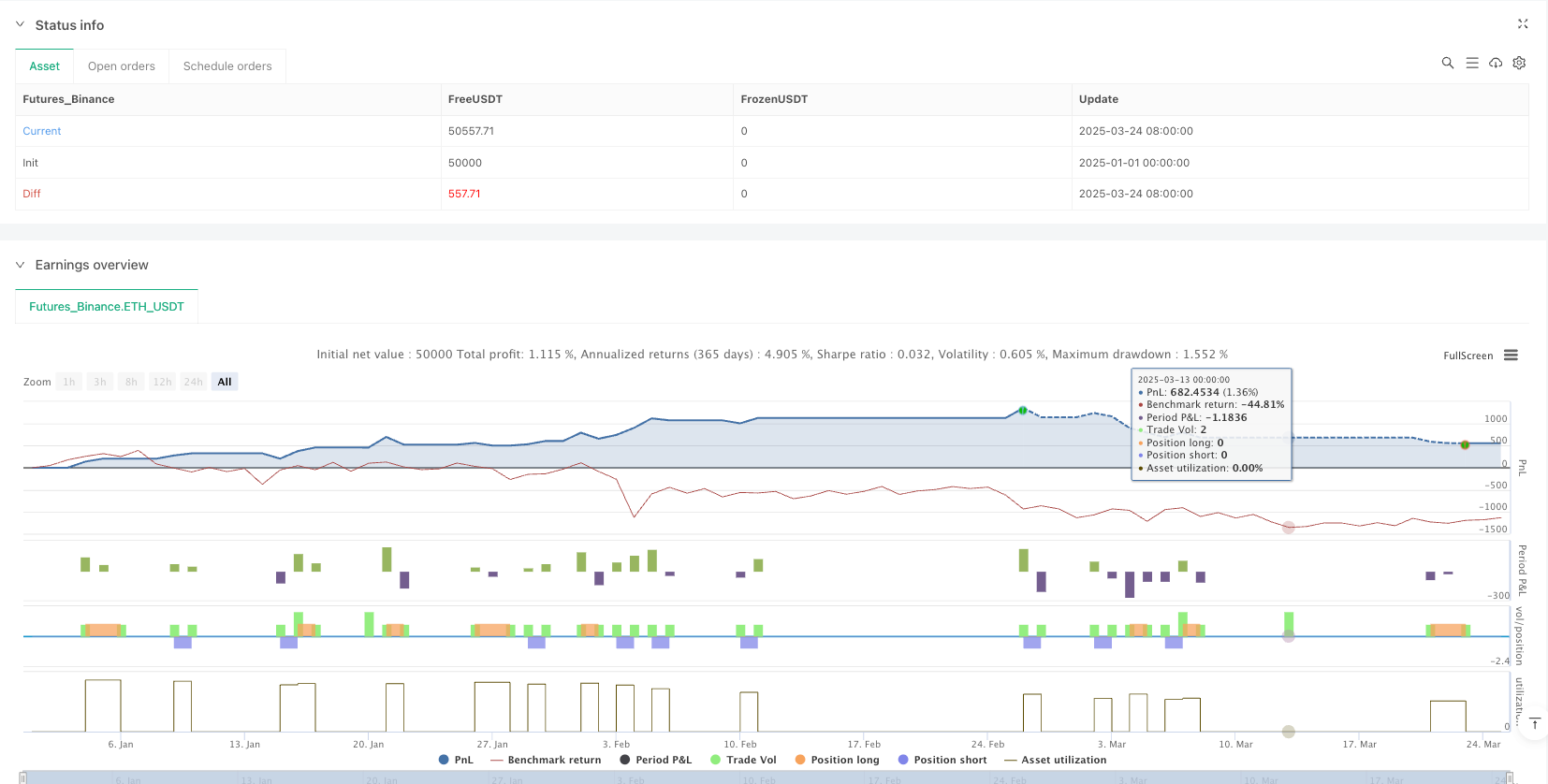
Aperçu

La stratégie de rupture dynamique d’ajustement des taux de volatilité de Black-Scholes est une méthode de négociation quantitative basée sur la statistique et la théorie de la tarification des options. Elle applique habilement les idées du modèle Black-Scholes à l’analyse des ruptures de prix du marché, en calculant les fluctuations historiques et en ajustant dynamiquement les intervalles de prix attendus, afin d’obtenir une capture intelligente des signaux de rupture.

Principe de stratégie

La stratégie fonctionne selon les étapes suivantes:

1. Calcul du taux de volatilité: Calculer d’abord le taux de rendement logarithmique des gains historiques[1])), puis calculer la différence standard de ces rendements parallèles en utilisant la période de rétroaction définie (la période par défaut est de 20 cycles) et l’annualiser (la période est de 252 jours de négociation par an, 390 minutes par jour, multipliée par la racine carrée du cycle de négociation).

2. Calcul des mouvements attendus: une méthode inspirée de Black-Scholes est utilisée pour calculer les variations de prix attendues pour chaque cycle de négociation.[1] * volatility * math.sqrt ((1 / periodsPerYear)) ̳ qui est en fait le taux de volatilité annuel converti en la variation attendue d’un seul cycle ̳

3. Définition d’une limite dynamique: définir les deux seuils suivants en fonction du prix de clôture précédent et de l’amplitude de déplacement prévue calculée[1] + expectedMove et lowerThreshold = close[1] - expectedMove）。

4. Génération de signaux de transaction: lorsque le prix de clôture actuel franchit la barre supérieure, un signal de multiplication est déclenché; lorsqu’il franchit la barre inférieure, un signal de coupe est déclenché.

5. Gestion des risques: la stratégie est automatiquement configurée sur la base d’un pourcentage de stop (défault 1%) et d’un stop (défault 2%) après l’entrée dans la transaction. Pour les positions multiples, le stop est configuré sur un pourcentage spécifié en dessous du prix d’entrée et le stop est configuré sur un pourcentage spécifié au-dessus.

Analyse des avantages

1. Adaptabilité dynamique: par rapport aux stratégies de rupture traditionnelles utilisant des prix ou des pourcentages fixes, cette stratégie ajuste dynamiquement les seuils de rupture en fonction des fluctuations réelles du marché et s’adapte mieux aux différentes conditions et environnements de marché.

2. Fondation statistique: la stratégie est basée sur des principes statistiques validés et la théorie de la tarification des options, utilisant des rendements logarithmiques et des calculs de l’écart-type, avec une base théorique solide.

3. Gestion automatique des risques: les mécanismes d’arrêt et de suspension intégrés assurent que chaque transaction a des mesures de contrôle des risques prédéfinies, évitant l’excès de détention ou l’expansion des pertes causées par des facteurs émotionnels.

4. Flexibilité des paramètres: l’utilisateur peut ajuster le cycle de rétractation des taux de volatilité, le pourcentage d’arrêt et de perte en fonction des différents marchés et des préférences de risque personnelles, ce qui rend la stratégie plus adaptable.

5. Efficacité du calcul: le calcul de la stratégie est relativement simple et direct, il ne nécessite pas de combinaisons complexes d’indicateurs, réduit le risque de suradaptation et améliore l’efficacité de l’exécution.

Analyse des risques

1. Risque de fausse rupture: le marché peut se retirer rapidement après une brève rupture de la marge, ce qui entraîne des signaux erronés et des coûts de transaction inutiles. Ce risque peut être réduit en ajoutant un mécanisme de confirmation (comme la nécessité d’une rupture d’une certaine durée ou une confirmation de volume combinée).

2. Erreur d’estimation de la volatilité: la volatilité historique ne permet pas nécessairement de prédire avec précision la volatilité future, en particulier lorsque les conditions du marché changent brusquement. La combinaison de la volatilité implicite ou l’utilisation de modèles de volatilité plus complexes tels que GARCH peut être envisagée pour améliorer la précision des prévisions.

3. Sensibilité aux paramètres: les performances de la stratégie peuvent être sensibles aux cycles de retournement des taux d’oscillation, aux paramètres de stop loss et de stop loss. Il est recommandé de faire un retour d’expérience et d’optimiser les paramètres pour trouver la meilleure combinaison de paramètres pour un marché particulier.

4. Performance du marché tendanciel: dans un marché tendanciel fort, les prix peuvent se maintenir dans une direction pendant une longue période, au-delà de la fourchette de fluctuation attendue, ce qui entraîne la perte de tendances importantes.

5. Effets sur le coût des transactions: des signaux de rupture fréquents peuvent entraîner des transactions excessives, augmentant les commissions et les coûts de points de glissement. La fréquence des transactions peut être réduite en définissant des intervalles de transaction ou des filtres de signaux.

Direction d’optimisation

1. Amélioration du calcul de la volatilité: les méthodes de calcul de la volatilité peuvent être explorées à l’aide d’une moyenne mobile pondérée (EWMA) ou d’un modèle GARCH, qui permettent de mieux capturer l’effet d’agrégation et les caractéristiques de changement de temps de la volatilité. Les codes d’amélioration peuvent être les suivants:

// EWMA波动率计算
alpha = 0.94  // 衰减因子
ewmaVar = 0.0
ewmaVar := alpha * ewmaVar[1] + (1 - alpha) * logReturn * logReturn
ewmaVol = math.sqrt(ewmaVar) * math.sqrt(periodsPerYear)

1. Mécanisme de confirmation du signal: ajout de confirmation de la quantité de transaction ou de confirmation de la dynamique des prix pour réduire le risque de fausse percée:

volumeConfirmation = volume > ta.sma(volume, 20) * 1.5
momentumConfirmation = ta.rsi(close, 14) > 50 for longCondition or < 50 for shortCondition
longCondition := longCondition and volumeConfirmation and momentumConfirmation

1. Système d’arrêt automatique: arrêt dynamique basé sur l’ATR pour mieux s’adapter aux fluctuations du marché:

atrPeriod = 14
atrMultiplier = 2
atrValue = ta.atr(atrPeriod)
dynamicStopLoss = atrMultiplier * atrValue

1. Filtrage temporel: Ajout d’un filtrage temporel afin d’éviter les heures d’ouverture et de fermeture du marché qui sont inhabituellement volatiles:

timeFilter = (hour >= 10 and hour < 15) or (hour == 15 and minute < 30)
longCondition := longCondition and timeFilter

1. Confirmation multi-périodes: filtre les signaux opposés à la tendance principale en examinant la direction des périodes de temps plus élevées:

higherTimeframeClose = request.security(syminfo.tickerid, "60", close)
higherTimeframeTrend = ta.ema(higherTimeframeClose, 20) > ta.ema(higherTimeframeClose, 50)
longCondition := longCondition and higherTimeframeTrend
shortCondition := shortCondition and not higherTimeframeTrend

Résumer

La stratégie de rupture dynamique d’ajustement de la volatilité de Black-Scholes est une stratégie de quantification innovante qui combine la théorie de la tarification des options avec la méthode traditionnelle de rupture de la négociation. Elle établit des seuils de négociation dynamiques en calculant la volatilité du marché et en la convertissant en une fourchette de variation des prix attendus, et s’adapte efficacement aux caractéristiques de la volatilité dans différentes conditions du marché.

Cependant, la stratégie est également confrontée à des défis tels que les fausses percées, les erreurs d’estimation de la volatilité et la sensibilité des paramètres. Des mesures d’optimisation telles que l’introduction d’améliorations dans le calcul de la volatilité, des mécanismes de confirmation de signal, la gestion dynamique des risques et l’analyse multi-cycle peuvent considérablement améliorer la stabilité et la fiabilité de la stratégie.

Dans l’ensemble, la stratégie de rupture dynamique d’ajustement de la volatilité de Black-Scholes représente une tentative efficace de combiner l’analyse technique traditionnelle avec la théorie financière moderne, offrant aux traders quantifiés un cadre de négociation doté d’une base théorique solide, d’une grande flexibilité et d’une facilité de mise en œuvre. Grâce à une optimisation continue et à des ajustements appropriés, la stratégie devrait être solide dans différentes conditions de marché.