Stratégie de prévision des séries chronologiques AR-GARCH

Pourquoi l’analyse technique traditionnelle échoue-t-elle dans un marché complexe ?

Dans le domaine du trading quantitatif, nous sommes souvent confrontés à la confusion de savoir pourquoi des stratégies basées sur des moyennes mobiles simples ou RSI fonctionnent bien dans certains environnements de marché, mais échouent fréquemment dans d’autres. La réponse réside dans la complexité des séquences de temps financières, car elles sont non seulement auto-corrélatives, mais aussi caractérisées par des taux de volatilité qui varient avec le temps.

La stratégie analysée aujourd’hui, qui combine habilement les modèles de régression automatique AR(2) et d’écarts conditionnels GARCH(1,1), tente de résoudre ce problème d’un point de vue statistique. Il ne s’agit pas d’une simple superposition d’indicateurs techniques, mais d’une exploration approfondie des caractéristiques de la séquence de temps financière.

Comment les modèles capturent-ils l’effet mémoire des prix ?

Le cœur de la stratégie réside dans l’application du modèle de l’auto-rétroactivité. Qu’est-ce que l’auto-rétroactivité? En termes simples, c’est l’utilisation du passé pour prédire le futur.

r_t = φ₁ × r_{t-1} + φ₂ × r_{t-2} + ε_t

Le code utilise l’équation de Yule-Walker pour résoudre les coefficients φ1 et φ2:

c0 = calcAutoCovariance(returns, 0, lengthReg) // 滞后0期自协方差
c1 = calcAutoCovariance(returns, 1, lengthReg) // 滞后1期自协方差  
c2 = calcAutoCovariance(returns, 2, lengthReg) // 滞后2期自协方差
phi1 = (c1 * c0 - c2 * c1) / denominator // 第一个自回归系数
phi2 = (c2 * c0 - c1 * c1) / denominator // 第二个自回归系数

L’avantage de cette méthode est qu’elle ne repose pas sur des jugements subjectifs, mais qu’elle permet aux données de “parler” d’elles-mêmes et de découvrir les régularités implicites dans la séquence des prix.

Pourquoi le modèle GARCH est-il plus efficace pour décrire le risque du marché ?

Les modèles AR ne sont pas suffisants, car les fluctuations des marchés financiers ne sont pas constantes. Nous savons tous que le phénomène de “fluctuation de la volatilité” est souvent accompagné de fortes fluctuations et que les périodes de calme durent souvent plus longtemps.

Le modèle GARCH ((1,1)) est conçu précisément pour cette caractéristique:

σ²_t = ω + α × ε²_{t-1} + β × σ²_{t-1}

La logique d’implémentation dans le code en témoigne clairement:

omega = (1 - adjustedAlpha - adjustedBeta) * longTermVar
garchVariance := omega + adjustedAlpha * math.pow(arResidual[1], 2) + adjustedBeta * garchVariance[1]

L’idée clé ici est que la condition actuelle dépend non seulement de l’écart-square du résidu de la période précédente (les chocs à court terme), mais aussi de l’écart-condition de la période précédente (la continuité à long terme). Le paramètre α contrôle l’impact des chocs à court terme, β contrôle la continuité des fluctuations.

Comment la logique de négociation de la stratégie peut-elle équilibrer les risques et les bénéfices ?

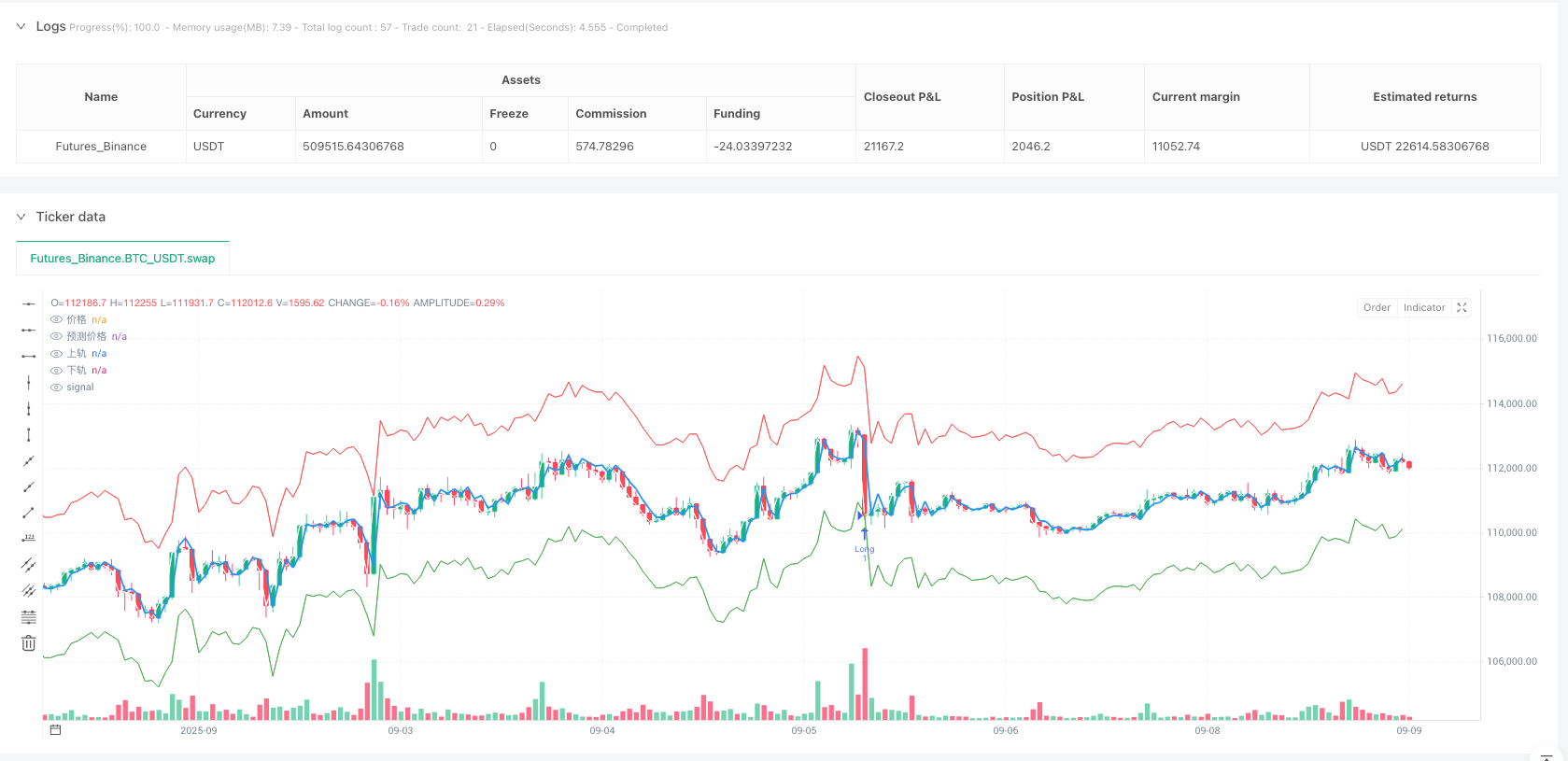
Avec les prévisions AR et les estimations de volatilité GARCH, la stratégie construit une zone de confiance dynamique:

upperReturnBand = arReturnPredict + stdevFactor * garchStd
lowerReturnBand = arReturnPredict - stdevFactor * garchStd

La logique de génération des signaux de transaction reflète l’idée de la régression de la moyenne:

• Il y a une tendance à la hausse lorsque le prix est en baisse (long signal = rawPrice < lowerPriceBand)
• Il y a une marge de manœuvre lorsque le prix franchit la bande supérieure.

La subtilité de cette conception réside dans le fait que la largeur de la zone de confiance s’adapte à la dynamique de la volatilité du marché. Pendant les périodes de forte volatilité, la zone s’élargit, réduisant la fréquence des transactions; pendant les périodes de faible volatilité, la zone se rétrécit, augmentant les opportunités de négociation.

Quels sont les points clés à prendre en compte dans la pratique ?

1. Vérification de la stabilité du modèle Le code contient des vérifications de stabilité importantes:

if stabilityCheck >= 0.99 or math.abs(phi2) >= 0.99
    scaleFactor = 0.95 / math.max(stabilityCheck, math.abs(phi2) + 0.01)

Cela assure la stabilité du modèle AR et évite des résultats prédictifs dispersés.

2. La contrainte de convergence des paramètres Le modèle GARCH exige que α + β < 1 pour garantir l’existence d’un écart à long terme:

if sumParam >= 0.999
    scale = 0.99 / sumParam

3. La nécessité d’un mécanisme de filtrage Les stratégies fournissent des options de filtrage RSI, ce qui est important dans les applications pratiques. Des modèles purement statistiques peuvent ignorer les caractéristiques tendancielles du marché, et l’ajout d’indicateurs techniques peut fournir des signaux de confirmation supplémentaires.

Limites de la stratégie et améliorations

Bien que cette tactique soit élégante en théorie, elle est néanmoins nécessaire dans la pratique:

Sélection des fréquences de donnéesLes modèles AR-GARCH varient considérablement selon les périodes. Les données à haute fréquence fournissent plus d’informations, mais introduisent également plus de bruit.

Variabilité temporelle des paramètres: Dans la réalisation actuelle, on suppose que les paramètres AR et GARCH sont constants dans la fenêtre d’estimation, mais que la structure du marché réel peut changer.

Effets sur le coût des transactionsLes stratégies d’arbitrage statistique nécessitent généralement une fréquence de transaction plus élevée, et les frais de transaction et les coûts de dérivation ne doivent pas être négligés.

Résumé: La valeur de la modélisation statistique dans les transactions quantifiées

Cette stratégie AR-GARCH montre la puissance de la statistique moderne dans la modélisation financière. Il ne s’agit pas d’une simple combinaison d’indicateurs techniques, mais d’une exploration approfondie des caractéristiques statistiques de la chronologie financière.

Pour les traders quantifiés, la valeur d’une compréhension de ce type de stratégie réside non seulement dans l’application directe, mais aussi dans la capacité à analyser le marché avec une pensée statistique. Aujourd’hui où l’IA et l’apprentissage automatique dominent, ces modèles statistiques classiques restent des pierres angulaires importantes pour notre compréhension des marchés et la construction de stratégies.