गॉस और ब्लैक स्वान

• काला हंस

  मेरे पास एक उपनाम है, जो कि पंख सिद्धांतवादी पंख है, जो शायद लोगों के लिए एक नाटक है, क्योंकि मैं वास्तव में बहुत बेवकूफ हूं, एक सिद्धांत को एक ढेर से सारांशित करना पसंद करता हूं। मैं आंकड़ों में निपुण हूं, मुझे अपने आस-पास की सभी चीजों के औसत का पता लगाना पसंद है, उनके पंखों के मूल पंखों को पकड़ना पसंद है, और सभी प्रकार के छोटे-छोटे विवरणों को अनदेखा करना, यह सोचकर कि केवल चीजों की समग्र प्रवृत्ति को पकड़ना, मेरे दिमाग में पंख सिद्धांत को जीवन में वास्तविकता में बदल सकता है, लेकिन वास्तविकता ने मुझे एक लकड़ी के पंख वाले मूर्ख के रूप में प्रशिक्षित किया है, यहां तक कि पकाया हुआ पंख भी उड़ जाएगा।

  मेरे पिताजी ने ज्यादा किताबें नहीं पढ़ी हैं, लेकिन वे एक प्रसिद्ध बुजुर्ग व्यक्ति हैं, जो वास्तविक जीवन में अक्सर आश्चर्यजनक जीत हासिल करते हैं।

  यह मुझे एक सिद्धांतकार के रूप में भ्रमित करता है, क्योंकि विवरण मेरे लिए रेडियो शोर की तरह अनदेखा करने योग्य हैं। मेरा विश्वास प्रसिद्ध गॉस वितरण से है (नीचे देखें) जो हमें बताता है कि जीत और हार व्यक्तिगत विवरणों पर नहीं, बल्कि समग्र गुणों पर निर्भर करती हैं। जैसे कि मैं एक डेट पर बिना पर्स के एक अनुभव के लिए एक प्रेमिका को खो सकता हूं, लेकिन मैं अपने जीवन में कई महिलाओं के साथ कई डेट पर जाऊंगा, और अगर मैं सामान्य रूप से अच्छा हूं, तो एक समग्र बैठक होगी।

  लेकिन पिताजी की बात सच साबित हुई।

  तो मैं सोच रहा था कि उस दुनिया में, जिस पर मुझे हमेशा गर्व रहा है, जो सुंदर गॉथस घंटों की वक्रों और न्यूटन के सामंजस्यपूर्ण नियमों से बनी है, क्या गलत है? मैंने जीव विज्ञान में प्रवेश किया और कृन्तकों की दुनिया में इसका जवाब पाया, क्योंकि एक जानवर - काला हंस।

  जब तक काला हंस नहीं आता, तब तक झील में तैरने वाले तिलों का रंग बर्फ से सफ़ेद होता था, और आप कल्पना कर सकते हैं कि उस नीले रंग की झील पर लाखों तिल उड़ते हैं, जो कि किली मजारो की बर्फ की तरह दिखते हैं। इसलिए मैंने सोचा कि यह सफेद हंस का प्रतीक है, और मैंने 100% संभावना के साथ भविष्यवाणी की कि सभी तिल सफेद थे। जब तक कि एक दिन एक शुद्ध काला हंस झील के ऊपर से उड़ता है, जैसे कि यह बाहरी दुनिया से आया था, तो यह मेरे तिल के सपने को तोड़ देता है। तब से मुझे एहसास हुआ कि जीवों की दुनिया में असाधारणताएं मूल रूप से होती हैं, औसत नहीं। असाधारणताएं हमेशा आपके अनुमान से अधिक संभावनाओं के साथ होती हैं, और पहले के सिद्धांतों को नष्ट कर देती हैं।

  शास्त्रीय भौतिकी की दुनिया औसत संख्याओं की दुनिया है, विवरण और विशेषताओं को हटा दिया जा सकता है। लेकिन जब जीवों के प्रभुत्व वाले क्षेत्र में प्रवेश किया जाता है, तो वे राजा बन जाते हैं।

  

गॉथिक कानूनों के अनुसार, एक दिन में चलने वाले एक नृत्य के लिए, हम गंदगी और जीवों की अराजकता में प्रवेश करने से पहले शोक व्यक्त करते हैं।

• गौस वितरण और लार्ज संख्या प्रमेय के औसत की शक्ति

  हम अक्सर चीजों की समग्र स्थिति को औसत से व्यक्त करते हैं, जैसे कि चीनी पुरुष की ऊंचाई 1 मीटर 7 है, और जो लोग आंकड़े बनाते हैं, उनके लिए औसत लगभग एक विश्वास बन जाता है, और हम अक्सर इस विश्वास के पीछे की मूलभूत धारणा को भूल जाते हैं - गौस वितरण, केवल जब हमारे आंकड़े गौस वितरण में होते हैं, तो औसत वास्तव में चीजों के गुणों का प्रतिनिधित्व कर सकता है।

  प्रारंभिक ज्ञान: जोड़ना औसत के बराबर होता है। औसत की गणना बहुत सारे डेटा को जोड़ने के बाद डेटा को विभाजित करने पर निर्भर करती है। औसत के आसपास के विचलन का आकार मानक विचलन द्वारा दर्शाया गया है। शास्त्रीय सिद्धांत हमें बताता है कि नमूना की क्षमता जितनी अधिक होगी, औसत अध्ययन समूह का प्रतिनिधित्व करने में उतना ही सक्षम होगा।

  

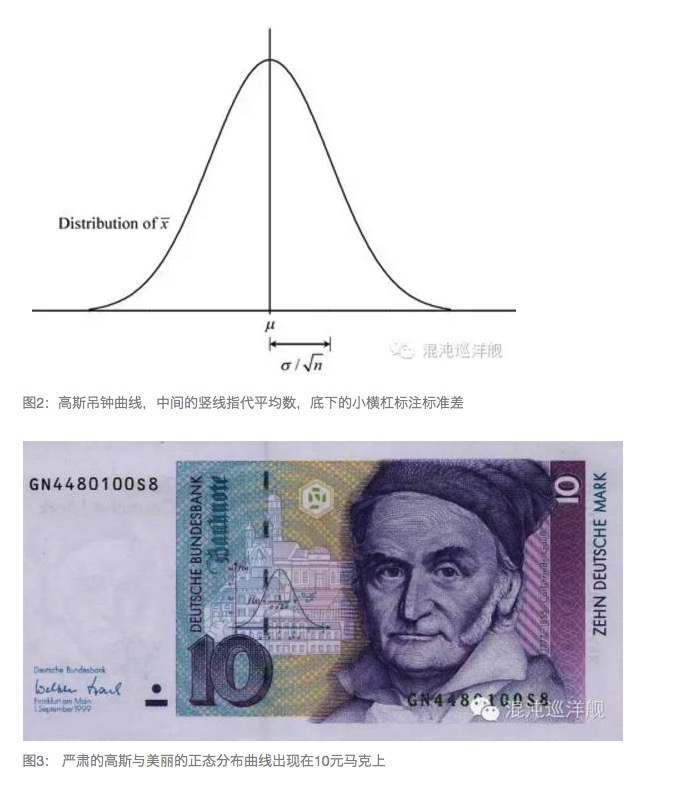
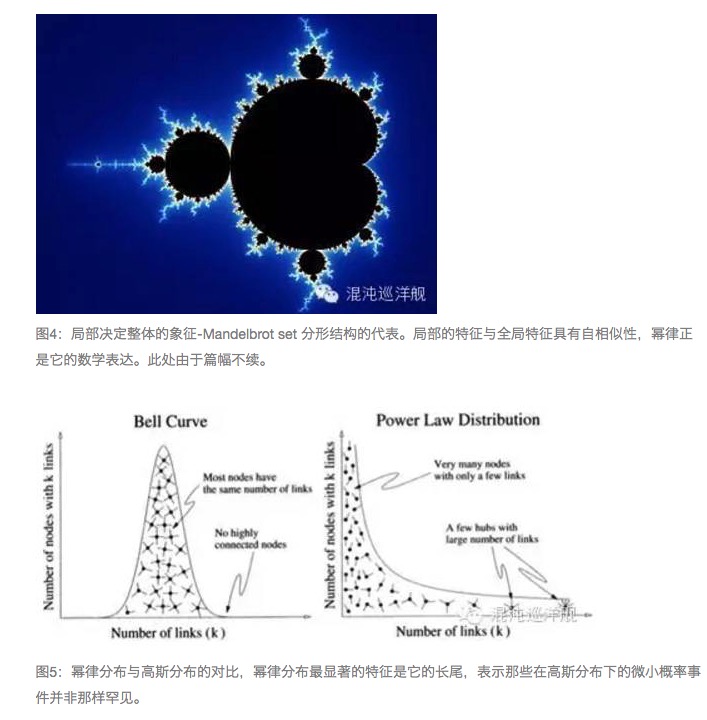
  Gauss ने हमें जोड़ने की शक्ति के बारे में बताया। एक यादृच्छिक घटना के लिए, जैसे कि कैसीनो में एक हाथी, हर बार एक से छह के परिणाम की पूरी तरह से भविष्यवाणी करना असंभव है, लेकिन यदि आप 10,000 बार दांव लगाते हैं, तो आप हर बार आपके द्वारा दिए गए अंकों को जोड़ते हैं, तो आप एक संख्या प्राप्त करते हैं जो अधिक से अधिक सटीक भविष्यवाणी की जा सकती है। इस परिणाम को Gauss वक्र के रूप में वर्णित किया जा सकता है, जिसमें दो विशेषताएं हैं, औसत और मानक विचलन। औसत एक समग्र प्रवृत्ति को दर्शाता है और मानक विचलन आपको अनिश्चितता की मात्रा बताता है। Gauss ने हमें बताया कि जैसे-जैसे संख्या बढ़ती है, मानक विचलन औसत के सामने अधिक से अधिक नगण्य हो जाता है, जब तक कि इसे अनदेखा नहीं किया जा सकता है, या अंतहीन जोड़ने के माध्यम से, जब एक यादृच्छिक घटना एक निश्चित घटना बन जाती है, तो हमें अधिक से अधिक सटीक औसत प्राप्त होता है। इसे बड़े संख्याओं का नियम कहा जाता है।

  

  बहुमत के नियम की शक्ति यह है कि वह एक निश्चित दुनिया को एक विशाल अनिश्चितता पर उत्पन्न कर सकता है। जैसे कि कल सूरज उगता है और वसंत फूलों को ऐसा करने की संभावना है, हम जानते हैं कि ऐसा नहीं होने की संभावना लगभग 0 है। वास्तव में, यह गौस वितरण और बहुमत के सिद्धांत की गारंटी है, क्योंकि सूर्य के फूलों को खोलने के लिए सूर्य और फूलों के असंख्य परमाणुओं और अणुओं के संयुक्त कार्य का परिणाम है, जब एक बार अनगिनत तंतुओं के साथ मिलकर काम करते हैं, तो तर्क यह सुनिश्चित करता है कि कुछ भी निश्चित रूप से उच्च सटीकता के साथ होगा। जैसे कि आपके पास बहुत सारे बेईमान सैनिक हैं, आप अभी भी युद्ध जीतने के लिए संख्या पर भरोसा कर सकते हैं।

  सामान्य वितरण और विशाल संख्या प्रमेय सभी निश्चितताओं की जड़ हैं, क्योंकि हमारा दृश्य जगत अनगिनत अनिश्चित सूक्ष्म कारकों के निरंतर योग का परिणाम है।

  विवरण के महत्व के बारे में रहस्योद्घाटनः वह हमें बताता है कि जब घटनाओं को निर्धारित करने के लिए पर्याप्त कारक होते हैं, तो परीक्षणों की संख्या पर्याप्त होती है, और हर चीज में, छोटे विवरण महत्वपूर्ण नहीं होते हैं क्योंकि वे एक विशाल राशि के योग में औसत दर्जे के होते हैं।

  लेकिन जल्दबाजी न करें।

• गॉस के नियम के पीछे का जाल

  A. विवरण कारक स्वतंत्र हैं

  यह थोड़ा अमूर्त लग सकता है, लेकिन वास्तव में यह है कि जो जोड़-घटित तत्व हैं वे एक दूसरे के साथ संवाद नहीं कर सकते हैं, जैसे कि अगर आप सभी महिलाओं को जानते हैं कि आप अच्छे या बुरे हैं, तो आपके द्वारा डेट किए जाने वाले लोगों में से अधिकांश को आदर्श औसत द्वारा निर्धारित परिणाम नहीं मिलेगा। क्योंकि सभी महिलाएं वास्तव में आपके द्वारा डेट किए गए लोगों के समान विचार प्राप्त करती हैं। आपको केवल एक बड़ा मानक अंतर मिलता है, और आपकी पहली तारीख की यादृच्छिकता को जीवन भर के परिणाम के रूप में बढ़ाया जाता है। प्रारंभिक प्रभाव की स्थिति को बढ़ाया जाता है, तथाकथित अमेज़ॅन वन में तितली के पंखे, एक तूफान को अटलांटिक पर ले जा रहा है।

  B. समय का स्थिरीकरण

  और यह थोड़ा अजीब है. उदाहरण के लिए, यदि आप एक बार एक सिक्का फेंकते हैं, और आप इसे बदल देते हैं, और आप एक सिक्का बदलते हैं, और फिर आप इसे बदल देते हैं, और फिर आप इसे बदल देते हैं, और फिर आप इसे बदल देते हैं, और फिर आप इसे बदल देते हैं, और फिर आप इसे बदल देते हैं, और फिर आप इसे बदल देते हैं, और फिर आप इसे बदल देते हैं, और फिर आप इसे बदल देते हैं, और फिर आप इसे बदल देते हैं, और फिर आप इसे बदल देते हैं, और फिर आप इसे बदल देते हैं, और फिर आप इसे बदल देते हैं, और फिर आप इसे बदल देते हैं, और फिर आप इसे बदल देते हैं, और फिर आप इसे बदल देते हैं, और फिर आप इसे बदल देते हैं, और फिर आप इसे बदल देते हैं, और फिर आप इसे बदल देते हैं, और फिर आप इसे बदल देते हैं।

  बहुसंख्यक प्रमेय हमारे यादृच्छिक दुनिया की समझ का आधार है, और यह हमें बताता है कि निश्चितता कैसे आकस्मिकता के आधार पर उभरती है। लेकिन न्यूटन के प्रथम नियम और आदर्श गैस मॉडल की तरह, चिकनी क्षैतिज और बिना बातचीत वाले बुनियादी कण वास्तविक जीवों की दुनिया में आभासी रूप से मौजूद नहीं हैं, हालांकि हमें कुछ समय के लिए कुछ समानताएं मिलती हैं।

• ब्लैक स्वान प्रभाव और ताल वितरण

  गॉस की वक्रता और विशाल संख्याओं के नियम एक भव्य सैद्धांतिक भौतिक दुनिया को नियंत्रित करते हैं, जहां अच्छे से अध्ययन करने से दिन-ब-दिन उन्नति होती है, और सीता निश्चित रूप से राजकुमार से मिलती है। लेकिन, ब्लैक स्वान ने एक परी कथा को नष्ट कर दिया।

  काला हंस का स्वभाव यह है कि व्यक्ति समग्र पर, विवरण समग्र पर निर्णायक प्रभाव डालता है। जब एक काला हंस पानी की सतह पर आता है, तो पूरे हंस समूह की विशेषताएं बदल जाती हैं, और एक शुद्ध सफेद विश्व हंस जब मध्य ग्रे हो जाता है। यहां, निश्चित रूप से, विशेष प्रभावों को देखने के लिए और अधिक है।

  Gauss के सकारात्मक दृष्टिकोण के अनुसार, एक काले रंग का हंस की संभावना को नजरअंदाज किया जा सकता था, क्योंकि हमने पहले एक विशाल दिन के रंग के नमूने की गणना की थी, लेकिन एक काले रंग का हंस अभी भी दिखाई दिया, और यह प्रतीत होता है कि यह एक अनपेक्षित संयोग था, हमारे लिए विशेष रूप से बुरा भाग्य? गलत। लेकिन गलत आप नहीं हैं, बल्कि एक सामान्य वितरण है।

  जीवों की दुनिया में, सत्ता-शक्ति वितरण-शक्ति कानून पर हावी है, जो वास्तव में अधिकार और धन से संबंधित है (चित्र 6, पैलेटो वितरण) । सत्ता-शक्ति वितरण की गणितीय अभिव्यक्ति सरल है, और विभिन्न सत्ता-शक्ति वितरण केवल सत्ता-शक्ति सूचकांक में भिन्नता पर प्रतिबिंबित होते हैं। यह गौस वितरण की प्रकृति से अलग है, जो कि गौस सामान्य वितरण के तहत संभावनाओं की छोटी से छोटी घटनाओं को अनदेखा करने के लिए है, लेकिन सत्ता-शक्ति वितरण के तहत यह दुर्लभ नहीं है। सत्ता-शक्ति के दृष्टिकोण से, ब्लैक स्वान की उपस्थिति समझ में आती है। दुर्लभ ब्लैक स्वान न केवल आते हैं, बल्कि समग्र रूप से निर्णय लेते हैं।

  

  

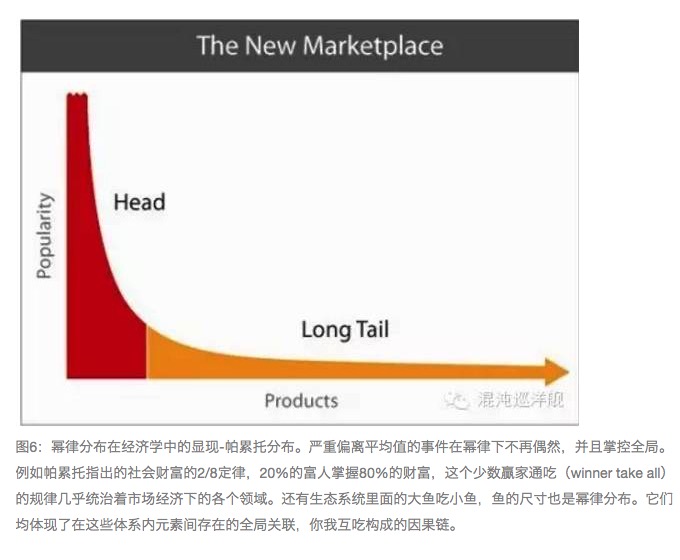
  क्यों एक ब्लैक स्वान प्रभाव इतना बड़ा है? - यहाँ आधुनिक भौतिकी में चरण परिवर्तन सिद्धांत एक चौंकाने वाला और शक्तिशाली जवाब देता है। मैं एक विशिष्ट उदाहरण के साथ एक हिमस्खलन का उल्लेख कर रहा हूं। हिमस्खलन एक पहाड़ी के शीर्ष पर एक बड़े क्षेत्र का बर्फ का गिरना है, जो कि एक हिमशैल के लिए लगभग असंभव है, जो क्लासिक ब्लैक स्वान घटना की परिभाषा को पूरा करता है, जो कि लगभग कभी नहीं होता है, और यदि यह होता है तो यह घातक है। हम वास्तव में अक्सर हिमस्खलन दुर्घटनाओं के बारे में क्यों सुनते हैं? क्योंकि हिमस्खलन का कारण वास्तव में इसके विपरीत है, बहुत छोटा है, शायद एक पत्थर के छोटे हिमशैल तक पहुंच सकता है, या एक व्यक्ति चिल्लाता है, और ये कारण दुर्लभ नहीं हैं। ये छोटे कारक ज्यादातर मामलों में हिमस्खलन पर कोई प्रभाव नहीं डालते हैं, लेकिन एक मामले में - यह हिमस्खलन की परिधि की स्थिति नहीं है, केवल जब यह निकटता की स्थिति में होता है।

  गंभीर स्थिति एक नाजुक संतुलन की स्थिति है, जो बर्फ के टुकड़े को एक साथ रखने की शक्ति और बर्फ के टुकड़े को विघटित करने की शक्ति के बराबर है, लेकिन जब तक कि तराजू थोड़ा झुका हुआ है, तब तक यह पूरी तरह से बदल नहीं सकता है। आप एक विशाल बर्फ की ढलान पर एक छोटे से पत्थर को फेंक देते हैं, पत्थर की प्रभावशीलता स्थानीय बर्फ द्वारा अवशोषित नहीं होती है, बल्कि पूरे बर्फ में फैल जाती है, जैसे कि एक मृत ऊंट के लिए अंतिम भूसे, जिससे संतुलन पूरी तरह से गिर जाता है।

  इस संकट की स्थिति ने ब्लैक स्वान को निर्णायक शक्ति बना दिया।

  

  हिमस्खलन सिद्धांत के मूल में महत्वपूर्ण स्थिति में विवरण की भूमिका का असीमित विस्तार (सकारात्मक प्रतिक्रिया) है। एक छोटा सा कारक जो केवल स्थानीय रूप से सीमित होता है, महत्वपूर्ण स्थिति में पूरे शरीर में फैल जाता है। हिमस्खलन सिद्धांत विभिन्न क्षेत्रों में फैलता है, जैसे कि भूकंप, शेयर बाजार में गिरावट, वित्तीय संकट, और यहां तक कि सामाजिक क्रांति का प्रकोप।

  किसी भी व्यक्ति की छोटी-छोटी भूमिकाओं को बढ़ाया जा सकता है और युद्ध को प्रभावित किया जा सकता है। उदाहरण के लिए, एक बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की बराबरी की

  जीवन-प्रवाह की प्रकृति एक विशेष परिवर्तनशीलता है। इसलिए जीवों से संबंधित सभी चीजें, जिनमें जीवों का इतिहास और हमारा मानव इतिहास और हम में से प्रत्येक का जीवन भी शामिल है, एक महत्वपूर्ण स्थिति में होती हैं, जो कि बड़े और छोटे हिमस्खलनों से भरा है, जो कि अप्रत्याशित विवरण है जो समग्र स्थिति को निर्धारित करता है। चूंकि आप कल जीवित हैं, एक काला हंस उड़ जाएगा। मूल रूप से, जीवन की उत्पत्ति, विकास, हमारे जन्म तक, काले हंस की एक श्रृंखला का परिणाम है, हम खुद एक काला हंस हैं, और हमें डर नहीं है कि यह कल फिर से आपकी खिड़की के सामने से गुजर जाएगा।

  नोट: जीवों का विकास सबसे मूल मूल का काला स्वान प्रभाव है, जीवों का परिवर्तन पहले से ही असाधारण है, और जो जीवित रहने में सक्षम है वह असाधारण है, और यह इस तरह की असाधारणता है, न कि मुख्यधारा (औसत) जीवों के विकास पर हावी है। हमारे दुनिया पर शासन करने वाले स्तनधारियों के पूर्वजों ने अरबों वर्षों तक उस समय के मुख्यधारा के क्रैपर्स (डायनासोर) की छाया में छिपे हुए थे, जब तक कि एक दिन, काला स्वान नहीं आया - एक तबाही ने क्रैपर्स के प्रभुत्व को समाप्त कर दिया ...।

  ब्लैक स्वान ने हमारे रोजमर्रा के जीवन में अनिश्चितता को गहराई से लाया है, और एक सिद्धांतकार के रूप में मुझे लगता है कि यह दुनिया, जिसमें सही रेखाएं, समानांतर रेखाएं, और न्यूटन के नियम हैं, एक खाली शहर की तरह है। इसका विशाल स्टील और सीमेंट, अभी भी आधुनिक उद्योगों को बनाए रखता है, यहां तक कि हमें ब्लैक स्वान के रहस्यों की खोज करने के लिए भी ले जाता है, लेकिन हमें खुद को जानने की अनुमति नहीं देता है।

• रहस्योद्घाटन

  • ब्लैक स्वान का सामना करना - अवसरों का सामना करना:

  जीवित रहना कठिन है. हमारी संस्कृति नायकों को प्रोत्साहित करती है, इतिहास वास्तव में बचे हुए लोगों द्वारा लिखा जाता है. अच्छा जीना, दिल खोलना, आँखें खोलना, सक्रिय तैयारी, आपके पास अपने काले रंग की प्रतीक्षा करने के लिए और अधिक अवसर हैं।

  • नकारात्मक ब्लैक स्वान - ताइवान जोखिम के साथः

  एक काले रंग का हंस की विशेषता यह है कि वह अंधेरे में छिपा रहता है, और जब तक वह आपके सामने नहीं आता है, तब तक आप नहीं जानते कि वह आपको पीछे से देख रहा है। यहाँ सोचकर मुझे डर नहीं लगता। क्योंकि ज्ञात तथाकथित जोखिम खतरनाक नहीं हैं, और आप वास्तविक जोखिम नहीं जानते हैं।

  • जोखिम नियंत्रण:

  जब एक नकारात्मक ब्लैक स्वान गिरता है, तो केवल एक चीज जो आप कर सकते हैं वह है इसके प्रभाव को सीमित करना और इसे हिमस्खलन में नहीं लाना।

  • शैक्षिक उपचार:

  फिर भी, गॉस को कम मत समझो, क्योंकि यहां तक कि पहेली वितरण को समझने के लिए गॉस को जानना आवश्यक है।

से अनुप्रेषित