रैखिक प्रतिगमन - न्यूनतम वर्ग विधि

• ### परिचय

इस समय के दौरान, मैंने सीखा कि कैसे एक मशीन को सीखा जा सकता है, और अध्याय 5 में लॉजिस्टिक रिवर्स को सीखा। यह काफी कठिन था। इस स्रोत को वापस ले जाकर, लॉजिस्टिक रिवर्स से लेकर रैखिक रिवर्स तक, और फिर न्यूनतम द्विपद विधि तक। अंत में, मैं उच्च गणित के अध्याय 9 के खंड 10 में न्यूनतम द्विपद विधि को सीखा, जिससे मुझे पता चलता है कि न्यूनतम द्विपद विधि के पीछे के गणितीय सिद्धांत कहां से आते हैं। न्यूनतम द्विगुणित एक प्रकार का कार्यान्वयन है जो इष्टतम समस्या में अनुभव सूत्रों को स्थापित करता है। इसके सिद्धांतों को समझना Logistic regression और समर्थन वेक्टर मशीनों के सीखने के के लिए उपयोगी है।

• ### पृष्ठभूमि

लघुतम द्विपद के इतिहास की पृष्ठभूमि बहुत ही रोचक है.

1801 में, इतालवी खगोलशास्त्री जुसेप पियाज़ी ने पहला क्षुद्रग्रह खोजा। 40 दिनों के बाद, पीएज़ी ने खोया क्योंकि यह सूर्य के पीछे चला गया था। इसके बाद, दुनिया भर के वैज्ञानिकों ने पियाज़ी के अवलोकन डेटा का उपयोग करके खोजा, लेकिन अधिकांश लोगों की गणना के आधार पर खोजा नहीं गया। उस समय 24 वर्षीय गॉस ने भी इसकी कक्षा की गणना की। ऑस्ट्रियाई खगोलशास्त्री हेनरी ओल्बर्स ने गॉस की गणना के आधार पर इसकी कक्षा की खोज की।

गॉस ने न्यूनतम द्विगुणन के लिए जिस विधि का उपयोग किया था, वह 1809 में उनकी पुस्तक में प्रकाशित हुई थी, जबकि फ्रांसीसी वैज्ञानिक लेजेंड ने 1806 में स्वतंत्र रूप से न्यूनतम द्विगुणन की खोज की थी, लेकिन चुपचाप चुपचाप चुपचाप चुपचाप चुपचाप चुपचाप चुपचाप चुपचाप चुपचाप चुपचाप चुपचाप चुपचाप चुपचाप चुपचाप चुपचाप चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके चुपके

1829 में, गॉस ने यह सिद्ध किया कि लघुतम द्विगुणन का अनुकूलन प्रभाव अन्य तरीकों से अधिक है, गॉस-मार्कोव प्रमेय देखें।

• ### तीसरा, ज्ञान का उपयोग

सबसे छोटा द्विगुणित गुणांक का मूल यह है कि सभी डेटा विचलन के वर्ग और न्यूनतम की गारंटी दी जाए।

मान लीजिए कि हम कुछ युद्धपोतों की लंबाई और चौड़ाई डेटा एकत्र करते हैं।

इस डेटा के आधार पर हमने पायथन में एक बिंदीदार नक्शा बनाया है:

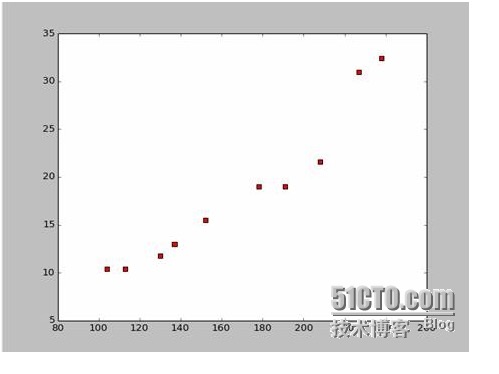
इस चित्र के लिए कोड इस प्रकार है:

  import numpy as np                # -*- coding: utf-8 -*
  import os
  import matplotlib.pyplot as plt
  def drawScatterDiagram(fileName): # 改变工作路径到数据文件存放的地方
      os.chdir("d:/workspace_ml")
      xcord=[];ycord=[]
      fr=open(fileName)
      for line in fr.readlines():
          lineArr=line.strip().split()
          xcord.append(float(lineArr[1]));ycord.append(float(lineArr[2]))
      plt.scatter(xcord,ycord,s=30,c='red',marker='s')
      plt.show()

अगर हम पहले दो बिंदुओं को लेते हैं, तो हमें दो समीकरण मिलते हैं. 152*a+b=15.5 328*a+b=32.4 तो हम a=0.197 और b=-14.48 को हल करते हैं. तो हम इस तरह के एक मिलान प्राप्त कर सकते हैंः

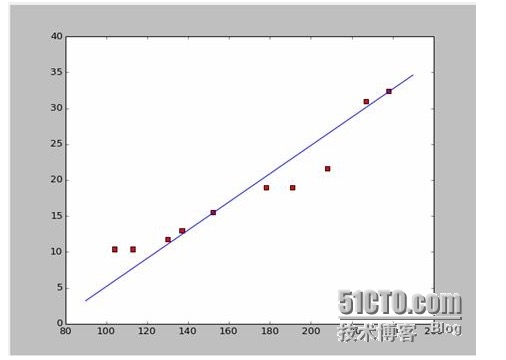
ठीक है, अब एक नया सवाल है, क्या a और b सबसे अच्छे समाधान हैं? और पेशेवर रूप से, क्या a और b मॉडल के लिए सबसे अच्छे पैरामीटर हैं? इस सवाल का जवाब देने से पहले, हम एक और सवाल हल करते हैं: a और b किस शर्त को पूरा करते हैं?

इसका उत्तर है कि यह सुनिश्चित करता है कि सभी आंकड़ों का वर्ग और न्यूनतम विचलन है। सिद्धांत के लिए, हम बाद में देखेंगे कि इस उपकरण का उपयोग कैसे करें सबसे अच्छा a और b की गणना करने के लिए।

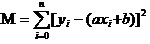
अब हम M के सबसे छोटे a और b को ढूँढते हैं. ध्यान दें कि इस समीकरण में, हम जानते हैं कि y और xi

तो यह एक द्विपद फलन है, जिसमें a, b, M अपने स्वयं के चर हैं.

याद कीजिये कि उच्च संख्याओं में कैसे एकवचन फलनों के लिए एकवचन फलनों का चरम होता है। हम इस उपकरण का उपयोग करते हैं। तो द्विवचन फलनों में, हम अभी भी एकवचन फलनों का उपयोग करते हैं। केवल यहाँ एकवचन फलनों के लिए एक नया नाम दिया गया है। एकवचन फलनों को दो चरों में से एक को निरंतर मानकर एकवचन फलन के लिए उपयोग किया जाता है। M के लिए पूर्णांक के माध्यम से, हम समीकरणों का एक सेट है

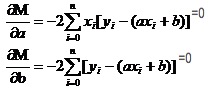
इन दोनों समीकरणों में x और y ज्ञात हैं.

यह बहुत आसान है a और b को खोजने के लिए। चूंकि यह विकिपीडिया डेटा है, इसलिए मैं सीधे उत्तरों का उपयोग करके एक उपयुक्त छवि बनाने के लिए यहां हूंः

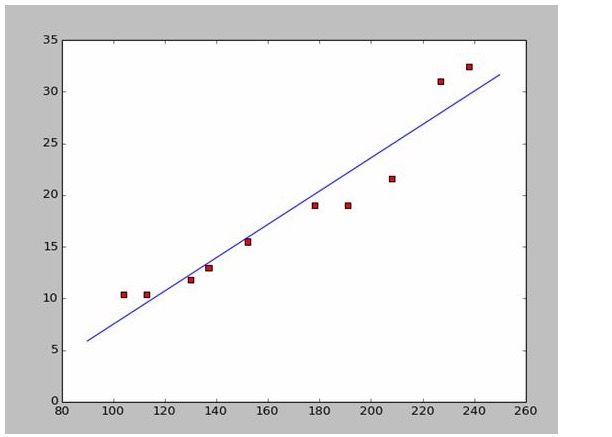
  # -*- coding: utf-8 -*importnumpy as npimportosimportmatplotlib.pyplot as pltdefdrawScatterDiagram(fileName):
  # 改变工作路径到数据文件存放的地方os.chdir("d:/workspace_ml")xcord=[];
  # ycord=[]fr=open(fileName)forline infr.readlines():lineArr=line.strip().split()xcord.append(float(lineArr[1]));
  # ycord.append(float(lineArr[2]))plt.scatter(xcord,ycord,s=30,c='red',marker='s')
  # a=0.1965;b=-14.486a=0.1612;b=-8.6394x=np.arange(90.0,250.0,0.1)y=a*x+bplt.plot(x,y)plt.show()
  # -*- coding: utf-8 -*
  import numpy as np
  import os
  import matplotlib.pyplot as plt
  def drawScatterDiagram(fileName):
      #改变工作路径到数据文件存放的地方
      os.chdir("d:/workspace_ml")
      xcord=[];ycord=[]
      fr=open(fileName)
      for line in fr.readlines():
          lineArr=line.strip().split()
          xcord.append(float(lineArr[1]));ycord.append(float(lineArr[2]))
      plt.scatter(xcord,ycord,s=30,c='red',marker='s')
      #a=0.1965;b=-14.486
      a=0.1612;b=-8.6394
      x=np.arange(90.0,250.0,0.1)
      y=a*x+b
      plt.plot(x,y)
      plt.show()

• ### चार सिद्धांतों की खोज

डेटा मिलान में, मॉडल पैरामीटर को अनुकूलित करने के लिए मॉडल के अनुमानित डेटा को वास्तविक डेटा के अंतर के वर्ग के बजाय पूर्ण मान और न्यूनतम क्यों दिया जाता है?

इस सवाल का जवाब पहले से ही दिया जा चुका है, लिंक पर देखें (http://blog.sciencenet.cn/blog-430956-621997.html)

व्यक्तिगत रूप से मुझे यह व्याख्या बहुत ही रोचक लगती है. विशेष रूप से इसके अंदर की परिकल्पना: सभी बिंदु जो f से अलग हैं (x) शोर हैं.

एक बिन्दु जितना दूर है, उतना ही शोर अधिक है, और यह बिन्दु होने की संभावना भी कम है। तो विन्दु की दूरी x और होने की संभावना f (x) के बीच क्या संबंध है?

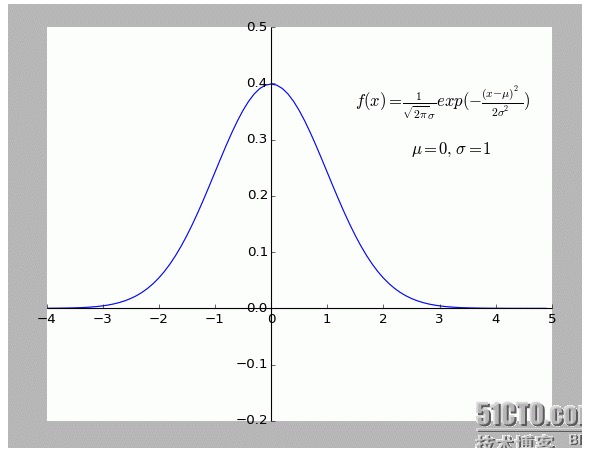
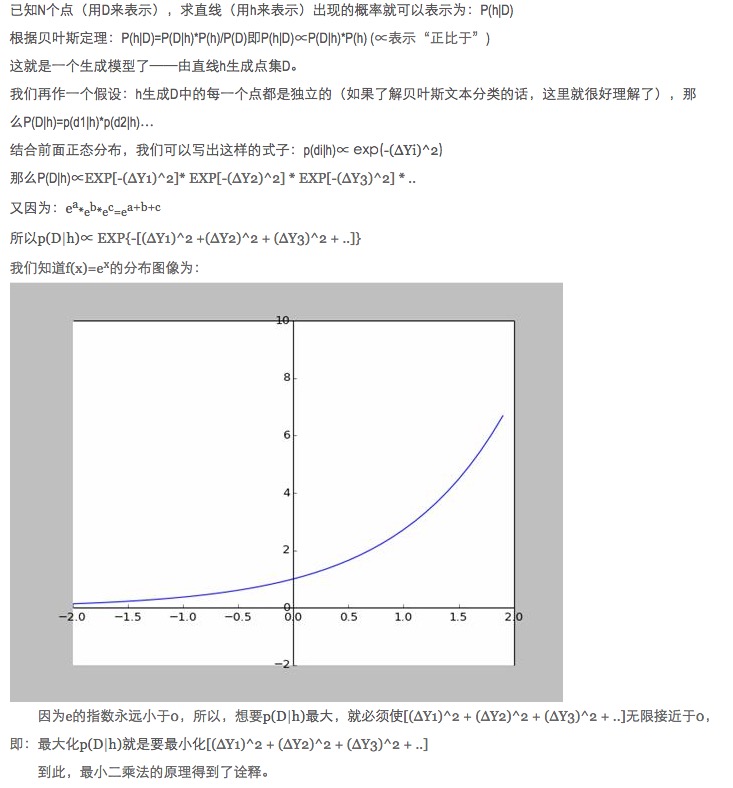
• ### पांच, विस्तार

उपरोक्त सभी दो आयामी स्थितियां हैं, यानी केवल एक स्वयं चर है। लेकिन वास्तविक दुनिया में अंतिम परिणाम को प्रभावित करने वाले कई कारकों का एक ओवरलैप है, यानी स्वयं चर की कई स्थितियां होंगी।

सामान्य N उपरेखीय फलनों के लिए, रैखिक बीजगणित की एक पंक्ति में उलटा मैट्रिक्स का उपयोग करना ठीक है; चूंकि कोई उपयुक्त उदाहरण नहीं मिला है, इसलिए इसे एक तर्क के रूप में छोड़ दें।

बेशक, प्रकृति में एक सरल रैखिकता की तुलना में एक बहुपद अनुकूलन अधिक है, और यह एक उच्च स्तर की सामग्री है।

• संदर्भ

  • उच्च गणित (छठा संस्करण) उच्च शिक्षा प्रकाशन)
  • बीजिंग यूनिवर्सिटी पब्लिकेशन
  • इंटरएक्टिव विश्वकोश:लघुतम द्विगुणन
  • विकिपीडियाः लघुतम द्विगुणन
  • साइंस नेटवर्क:सबसे छोटा द्विगुणित?

मूल रचना, पुनर्प्रकाशित करने की अनुमति, पुनर्प्रकाशित करते समय कृपया लेख के मूल स्रोत, लेखक की जानकारी और इस घोषणा को हाइपरलिंक के रूप में इंगित करें। अन्यथा कानूनी जिम्मेदारी होगी। http://sbp810050504.blog.51cto.com/2799422/1269572