नैवे बेयस की रोचक समझ

NavieBayes

  जीवन में कई अवसरों में वर्गीकरण की आवश्यकता होती है, जैसे कि समाचार वर्गीकरण, रोगी वर्गीकरण और अन्य व्यावहारिक उपयोग के परिदृश्य। ताकि आप समझ सकें कि आप क्या कल्पना कर सकते हैं, इस लेख में व्यावहारिक अनुप्रयोगों से एक सरल सामान्य वर्गीकरण एल्गोरिथ्म का परिचय दिया गया है - सरल बेयज़ (Navie Bayes classifier) ।

• 01 रोगी वर्गीकरण के उदाहरण

मैं एक उदाहरण के साथ शुरू करूँगा, और आप देखेंगे कि बेयज़ वर्गीकरण बहुत आसान है। एक अस्पताल ने सुबह में छह मरीजों को भर्ती किया, जैसा कि नीचे दी गई तालिका में दिखाया गया है।

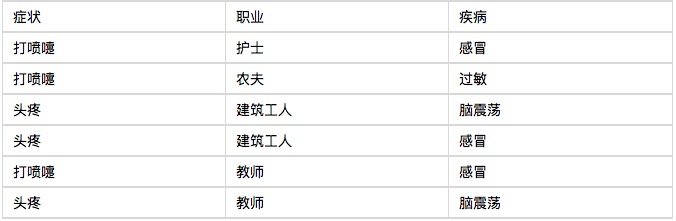
अब सातवां मरीज आया है, एक कंस्ट्रक्शन वर्कर जो छींक रहा है। पूछिए कि उसे सर्दी होने की कितनी संभावना है? बेयज़ के सिद्धांत के अनुसारः

  P(A|B) = P(B|A) P(A) / P(B)

क्या आप जानते हैं?

  P(感冒|打喷嚏x建筑工人) 
  　　　　= P(打喷嚏x建筑工人|感冒) x P(感冒) 
  　　　　/ P(打喷嚏x建筑工人)

मान लीजिये कि “स्पिट” और “बिल्डिंग वर्कर” स्वतंत्र हैं, इसलिए उपरोक्त समीकरण बन जाता है

  P(感冒|打喷嚏x建筑工人) 
  　　　　= P(打喷嚏|感冒) x P(建筑工人|感冒) x P(感冒)
  　　　　/ P(打喷嚏) x P(建筑工人)

यह गणना योग्य है।

  P(感冒|打喷嚏x建筑工人) 
  　　　　= 0.66 x 0.33 x 0.5 / 0.5 x 0.33 
  　　　　= 0.66

इस प्रकार, एक निर्माण श्रमिक जो छींकता है, उसके लिए 66% संभावना है कि उसे सर्दी हो गई है। इसी तरह, यह भी संभव है कि रोगी को एलर्जी या आघात हो। इन संभावनाओं की तुलना करके, यह पता लगाया जा सकता है कि उसे कौन सी बीमारी हो सकती है।

यह बेयज़ वर्गीकरण की मूल विधि है: कुछ विशेषताओं के आधार पर, सांख्यिकीय डेटा के आधार पर, विभिन्न श्रेणियों की संभावनाओं की गणना करें, ताकि वर्गीकरण किया जा सके।

• 02 सरल बेयज़ वर्गीकरण के सूत्र

मान लीजिए कि किसी व्यक्ति के पास n विशेषताएं हैं, क्रमशः F1, F2, … , Fn … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … . .

  P(C|F1F2...Fn) 
  　　   = P(F1F2...Fn|C)P(C) / P(F1F2...Fn)

चूंकि P ((F1F2…Fn) सभी श्रेणियों के लिए एक ही है, इसे छोड़ दिया जा सकता है, और यह प्रश्न बन जाता है

  P(F1F2...Fn|C)P(C)

अधिकतम

एक सरल बेयज़ वर्गीकरण एक कदम आगे है, यह मानते हुए कि सभी विशेषताएं एक-दूसरे से स्वतंत्र हैं, और इसलिए

  P(F1F2...Fn|C)P(C) 
  　　   = P(F1|C)P(F2|C) ... P(Fn|C)P(C)

उपरोक्त समीकरण के दाईं ओर स्थित प्रत्येक तत्व को सांख्यिकीय डेटा से प्राप्त किया जा सकता है, जिससे प्रत्येक श्रेणी के अनुरूप होने की संभावना की गणना की जा सकती है, जिससे सबसे अधिक संभावना वाली श्रेणी का पता लगाया जा सकता है।

हालांकि “सभी विशेषताएं एक-दूसरे से स्वतंत्र हैं” की धारणा वास्तविकता में लागू होने की संभावना नहीं है, यह गणना को काफी सरल बनाती है, और अध्ययनों से पता चलता है कि वर्गीकरण परिणामों की सटीकता पर इसका बहुत कम प्रभाव पड़ता है।

सरल बेयज़ वर्गीकरण का उपयोग करने के लिए नीचे दो उदाहरण दिए गए हैं।

• 03 खाता वर्गीकरण

एक सामुदायिक वेबसाइट के अनुसार, 10,000 खातों में से 89% असली हैं (C0 पर सेट करें) और 11% फर्जी हैं (C1 पर सेट करें) ।

  C0 = 0.89 C1 = 0.11

मान लीजिए कि एक खाते में निम्नलिखित तीन विशेषताएं हैं F1: लॉग की संख्या/ पंजीकरण के दिन F2: दोस्तों की संख्या/ पंजीकरण के दिन F3: क्या असली हेड इमेज का उपयोग किया जा सकता है (असली हेड इमेज 1, गैर-असली हेड इमेज 0) F1 = 0.1  F2 = 0.2  F3 = 0

कृपया पूछें कि क्या यह खाता वास्तविक है या नकली है? यह सरल बेयज़ वर्गीकरण का उपयोग करके किया जाता है और निम्नलिखित गणना के लिए गणना की जाती है:

P(F1|C)P(F2|C)P(F3|C)P©

यद्यपि उपरोक्त मानों को आंकड़ों से प्राप्त किया जा सकता है, लेकिन यहाँ एक समस्या हैः F1 और F2 निरंतर चर हैं, इसलिए किसी विशेष मान के आधार पर गणना की संभावना उपयुक्त नहीं है। एक चाल यह है कि निरंतर मानों को अलग-अलग मानों में परिवर्तित किया जाए और अंतराल की संभावनाओं की गणना की जाए। उदाहरण के लिए, F1 को[0, 0.05]、(0.05, 0.2)、[0.2, +∞] तीन खंडों में, और फिर प्रत्येक खंड की संभावनाओं की गणना. हमारे उदाहरण में, F1 0.1 के बराबर है, जो दूसरे खंड में है, इसलिए हम गणना करते समय दूसरे खंड की संभावनाओं का उपयोग करते हैं.

आंकड़ों के अनुसारः

P(F1|C0) = 0.5, P(F1|C1) = 0.1  P(F2|C0) = 0.7, P(F2|C1) = 0.2  P(F3|C0) = 0.2, P(F3|C1) = 0.9

इसलिए

P(F1|C0) P(F2|C0) P(F3|C0) P(C0)  = 0.5 x 0.7 x 0.2 x 0.89  = 0.0623 P(F1|C1) P(F2|C1) P(F3|C1) P(C1)  = 0.1 x 0.2 x 0.9 x 0.11  = 0.00198 जैसा कि आप देख सकते हैं, भले ही इस उपयोगकर्ता ने असली तस्वीर का उपयोग नहीं किया है, लेकिन यह 30 गुना अधिक संभावना है कि वह एक वास्तविक खाता है, जो एक नकली से अधिक है, इसलिए यह खाता वास्तविक है।

• 04 लिंग वर्गीकरण

नीचे मानव शरीर के लक्षणों के एक समूह के बारे में आंकड़े दिए गए हैं।

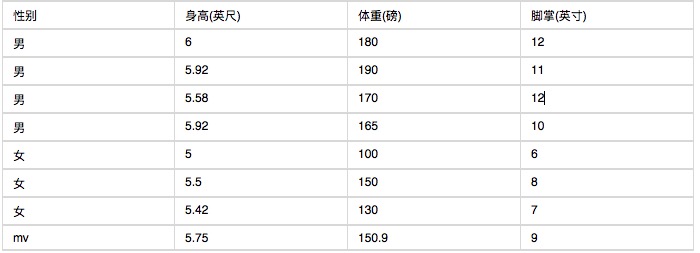
यदि कोई व्यक्ति 6 फीट लंबा, 130 पाउंड का वजन, और 8 इंच की पांव के साथ जाना जाता है, तो कृपया पूछें कि क्या वह पुरुष या महिला है? सरल बेयज़ वर्गीकरण के अनुसार, निम्नलिखित सूत्र के मानों की गणना करें।

पी (ऊंचाई और लिंग) एक्स पी (वजन और लिंग) एक्स पी (पैर और पैर और लिंग) एक्स पी (लिंग)

यहाँ कठिनाई यह है कि चूंकि ऊँचाई, वजन और पांव लगातार चर हैं, इसलिए पृथक चर विधि का उपयोग नहीं किया जा सकता है। और चूंकि बहुत कम नमूने हैं, इसलिए इसे अंतराल पर नहीं किया जा सकता है। यह कैसे किया जाता है? इस मामले में, यह माना जा सकता है कि पुरुषों और महिलाओं की ऊँचाई, वजन और पांव एक सामान्य वितरण है, और नमूने के माध्यम से औसत और अंतर की गणना की जाती है, जो कि एक सामान्य वितरण घनत्व फ़ंक्शन है। घनत्व फ़ंक्शन के साथ, आप एक बिंदु पर घनत्व फ़ंक्शन के मूल्य की गणना करने के लिए मूल्यों को जोड़ सकते हैं। उदाहरण के लिए, पुरुषों की औसत ऊँचाई 5.855 है, और अंतर 0.035 है।

इन आंकड़ों के साथ, लिंग वर्गीकरण की गणना की जा सकती है।

P (ऊंचाई = 6 आयु वर्ग के पुरुष) x P (वजन = 130 आयु वर्ग के पुरुष) x P (पांव = 8 आयु वर्ग के पुरुष) x P (पुरुष)

= 6.1984 x e-9

P (ऊंचाई = 6 सज्जन महिला) x P (वजन = 130 सज्जन महिला) x P (पांव = 8 सज्जन महिला) x P (महिला)

= 5.3778 x e-4

जैसा कि आप देख सकते हैं, महिलाओं में पुरुषों की तुलना में लगभग 10,000 गुना अधिक संभावना है, इसलिए यह एक महिला है।

वीकेसी के सार्वजनिक नंबर से लिया गया