छिपा हुआ मार्कोव मॉडल

• ### 1. पहचान

आज हम स्टॉक में एचएमएम के सरल अनुप्रयोगों के बारे में बात करेंगे।

और अगर हम पहले से ही नहीं जानते हैं कि यह क्या है, तो हम एक कदम पीछे ले जाते हैं और पहले मारकोव श्रृंखला को देखते हैं।

मार्कोव श्रृंखला, जिसका नाम आंद्रेई मार्कोव (ए.ए. मार्कोव, 1856-1922) के नाम पर रखा गया है, गणित में मार्कोविक प्रकृति की एक अलग-अलग घटना की यादृच्छिक प्रक्रिया है। वर्तमान ज्ञान या जानकारी के संदर्भ में, अतीत (यानी वर्तमान से पहले की ऐतिहासिक स्थिति) भविष्य की भविष्यवाणी करने के लिए अप्रासंगिक है (यानी वर्तमान के बाद की भविष्य की स्थिति) ।

इस प्रक्रिया में, प्रत्येक राज्य का स्थानांतरण केवल पूर्ववर्ती n राज्यों पर निर्भर करता है, इस प्रक्रिया को 1n-वर्ग के मॉडल के रूप में जाना जाता है, जहां n स्थानांतरण राज्यों की संख्या को प्रभावित करता है। सबसे सरल मार्कोव प्रक्रिया एक चरण प्रक्रिया है, प्रत्येक राज्य का स्थानांतरण केवल उसके पूर्ववर्ती राज्य पर निर्भर करता है।

• ### उदाहरण दो

गणित में, यह इस तरह दिखता हैः

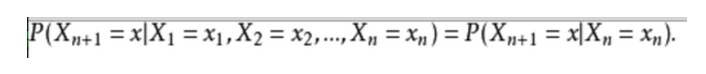
एक उदाहरण के लिए, हम चाहते हैं कि भविष्य के मौसम की भविष्यवाणी वर्तमान मौसम की स्थिति के आधार पर की जाए। एक तरीका यह है कि हम मान लें कि इस मॉडल की प्रत्येक स्थिति केवल पिछली स्थिति पर निर्भर करती है, जो कि मार्कोव की धारणा है, जो कि इस समस्या को काफी हद तक सरल बनाती है। बेशक, यह उदाहरण कुछ हद तक अव्यावहारिक भी है। लेकिन, इस तरह की एक सरलीकृत प्रणाली हमारे विश्लेषण के लिए फायदेमंद हो सकती है, इसलिए हम आमतौर पर इस तरह की मान्यताओं को स्वीकार करते हैं क्योंकि हम जानते हैं कि इस तरह की प्रणाली हमें कुछ उपयोगी जानकारी प्रदान कर सकती है, हालांकि यह बहुत सटीक नहीं है।

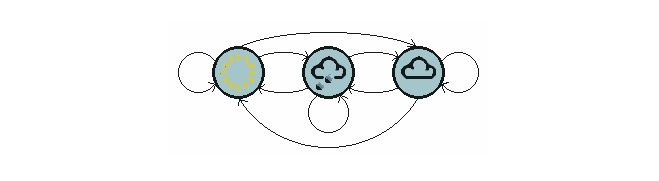
उपरोक्त चित्र मौसम के परिवर्तन के मॉडल को दर्शाता है।

ध्यान दें कि एक चरण प्रक्रिया जिसमें N अवस्थाएँ होती हैं, उनमें N2 अवस्थाओं के परिवर्तन होते हैं। प्रत्येक परिवर्तन की संभावना को स्थिति परिवर्तन की संभावना कहा जाता है, जो एक स्थिति से दूसरी स्थिति में परिवर्तन की संभावना है। इन सभी N2 संभावनाओं को एक राज्य परिवर्तन मैट्रिक्स द्वारा दर्शाया जा सकता है, जैसा कि ऊपर दिए गए मौसम के उदाहरण में राज्य परिवर्तन मैट्रिक्स में हैः

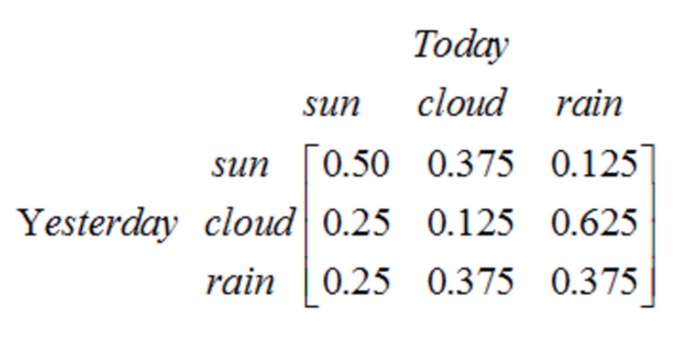
यह मैट्रिक्स बताता है कि यदि कल बादल छाए थे, तो आज 25% संभावना है कि यह दिन साफ रहेगा, 12.5% संभावना है कि यह बादल छाए रहेंगे, 62.5% संभावना है कि बारिश होगी, और यह स्पष्ट है कि मैट्रिक्स में प्रत्येक पंक्ति का योग 1 है।

इस तरह की एक प्रणाली को आरंभ करने के लिए, हमें एक आरंभिक संभाव्यता वेक्टर की आवश्यकता होती हैः

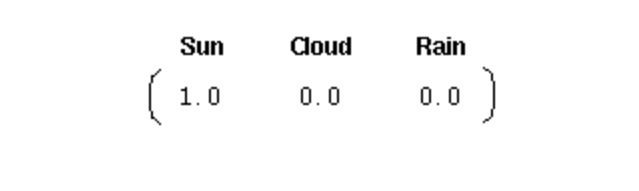
यह वेक्टर पहले दिन को एक दिन के रूप में दर्शाता है। यहाँ, हमने ऊपर दिए गए मार्कोव प्रक्रिया के लिए निम्नलिखित तीन भागों को परिभाषित किया हैः

स्थितिः दिन, बादल और बारिश।

प्रारंभिक वेक्टरः समय 0 पर सिस्टम की स्थिति की संभावना को परिभाषित करता है।

राज्य-परिवर्तन मैट्रिक्सः प्रत्येक मौसम परिवर्तन की संभावना सभी प्रणालियों को इस तरह से वर्णित किया जा सकता है एक मार्कोव प्रक्रिया

हालांकि, जब मार्कोव प्रक्रिया पर्याप्त शक्तिशाली नहीं होती है, तो हम क्या करते हैं? कुछ मामलों में, मार्कोव प्रक्रियाएं उन पैटर्न का वर्णन करने के लिए पर्याप्त नहीं हैं जिन्हें हम ढूंढना चाहते हैं।

उदाहरण के लिए हमारे शेयर बाजार, अगर केवल बाजार का अवलोकन, हम केवल उस दिन की कीमत, लेनदेन की मात्रा आदि जानकारी पता कर सकते हैं, लेकिन पता नहीं है कि वर्तमान में शेयर बाजार में क्या स्थिति है ((बैल बाजार, भालू बाजार, झटके, उछाल, आदि), इस मामले में हम दो राज्यों के सेट है, एक अवलोकन राज्य के सेट ((स्टॉक बाजार की कीमतों का लेनदेन राज्य, आदि) और एक छिपे हुए राज्य के सेट ((स्टॉक बाजार की स्थिति)) । हम एक एल्गोरिथ्म है कि शेयर बाजार की स्थिति का अनुमान लगाने के लिए स्टॉक बाजार की कीमतों का लेनदेन स्थिति और मार्कोव परिकल्पना के आधार पर खोज करने के लिए चाहते हैं ।

उपरोक्त सभी स्थितियों में, अवलोकन योग्य अवस्था क्रम और छिपी हुई अवस्था क्रम संभावना से संबंधित होते हैं। इसलिए हम इस प्रकार की प्रक्रिया को एक छिपी हुई मार्कोव प्रक्रिया और इस छिपी हुई मार्कोव प्रक्रिया की संभावना से संबंधित और अवलोकन योग्य अवस्थाओं के एक समूह के रूप में मॉडल कर सकते हैं, जो छिपी हुई मार्कोव मॉडल है।

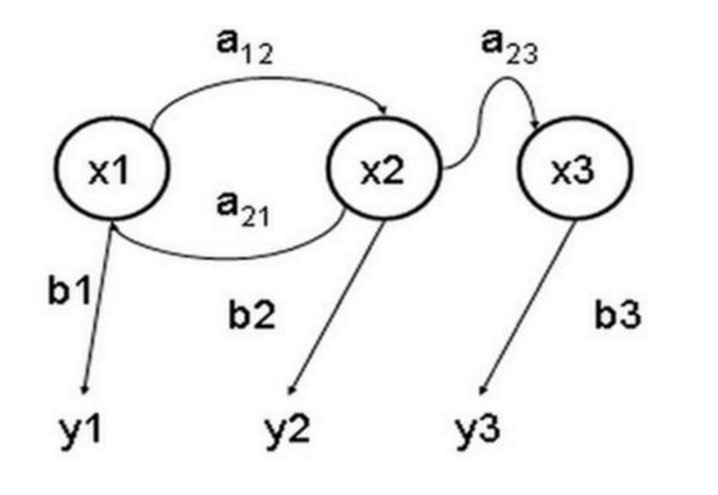
छुपे हुए मार्कोव मॉडल एक सांख्यिकीय मॉडल है जिसका उपयोग एक मार्कोव प्रक्रिया का वर्णन करने के लिए किया जाता है जिसमें अज्ञात पैरामीटर शामिल होते हैं। इसकी कठिनाई अवलोकन योग्य पैरामीटर से प्रक्रिया के निहित पैरामीटर को निर्धारित करना है, और फिर इन पैरामीटरों का उपयोग आगे के विश्लेषण के लिए करना है। नीचे एक तीन-राज्य छुपे हुए मार्कोव मॉडल राज्य स्थानांतरण ग्राफ है, जिसमें x निहित राज्य है, y अवलोकन योग्य आउटपुट है, a राज्य रूपांतरण संभावना है, और b आउटपुट संभावना है।

एक उदाहरण के रूप में, मान लीजिए कि मेरे हाथ में तीन अलग-अलग कंगन हैं। पहला कंगन हमारे सामान्य कंगन है (इस कंगन को D6 कहें), 6 पक्षों के साथ, प्रत्येक पक्ष (1,2,3,4,5,6) की संभावना ¹⁄₆ है। दूसरा कंगन एक चौतरफा है (इस कंगन को D4 कहें), प्रत्येक पक्ष (1,2,3,4) की संभावना ¹⁄₄ है। तीसरे कंगन में आठ पक्ष हैं (इस कंगन को D8 कहें), और प्रत्येक पक्ष (1,2,3,4,5,6,7,8) की संभावना ¹⁄₈ है।

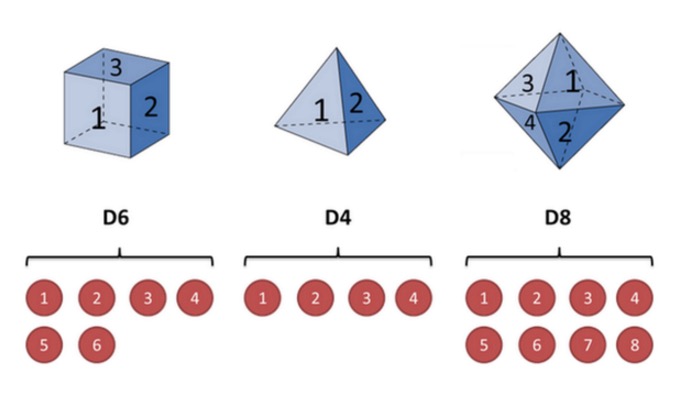
मान लीजिये कि हम एक गड्ढे से शुरू करते हैं, और हम तीन गड्ढों में से एक को चुनते हैं, और प्रत्येक गड्ढे को चुनने की संभावना ¹⁄₃ है। और फिर हम गड्ढे में डालते हैं, और हमें एक संख्या मिलती है, 1, 2, 3, 4, 5, 6, 7, 8 में से एक। और हम इस प्रक्रिया को बार-बार दोहराते हैं, और हमें एक संख्या मिलती है, और प्रत्येक संख्या 1, 2, 3, 4, 5, 6, 7, 8 में से एक है। उदाहरण के लिए, हम इस तरह की संख्या प्राप्त कर सकते हैं (गड्ढे में 10 बार): 1 6 3 5 2 7 3 5 2 4

इस संख्या को दृश्य अवस्था श्रृंखला कहते हैं। लेकिन अदृश्य मार्कोव मॉडल में, हमारे पास न केवल दृश्य अवस्था श्रृंखला है, बल्कि अदृश्य अवस्था श्रृंखला भी है। इस उदाहरण में, अदृश्य अवस्था श्रृंखला आपके द्वारा उपयोग की जाने वाली छड़ों की श्रृंखला है। उदाहरण के लिए, अदृश्य अवस्था श्रृंखला हो सकती हैः

सामान्य तौर पर, एचएमएम में कहा गया मार्कोव श्रृंखला वास्तव में छिपी हुई स्थिति श्रृंखला को संदर्भित करता है, क्योंकि छिपी हुई स्थिति के बीच रूपांतरण की संभावना है। हमारे उदाहरण में, डी 6 की अगली स्थिति डी 4, डी 6, डी 8 की संभावना ¹⁄₃ है। डी 4, डी 8 की अगली स्थिति डी 4, डी 6, डी 8 की रूपांतरण संभावना ¹⁄₃ है। इस तरह से सेट करना आसान है, लेकिन हम वास्तव में रूपांतरण की संभावना को यादृच्छिक रूप से सेट कर सकते हैं। उदाहरण के लिए, हम यह परिभाषित कर सकते हैं कि डी 6 के पीछे डी 4 नहीं है, डी 6 के पीछे डी 6 की संभावना 0.9 है, डी 8 की संभावना 0.1 है। इस तरह एक नया एचएमएम है।

इसी तरह, हालांकि दृश्य स्थिति के बीच कोई रूपांतरण संभावना नहीं है, लेकिन अंतर्निहित स्थिति और दृश्य स्थिति के बीच एक संभावना है जिसे आउटपुट संभावना कहा जाता है। हमारे उदाहरण के लिए, छह-पक्षीय बक्से ((D6) में 1 के उत्पादन की संभावना ¹⁄₆ है। 2, 3, 4, 5, 6 के उत्पादन की संभावना भी ¹⁄₆ है। हम आउटपुट संभावना को अन्य परिभाषाओं के रूप में भी कर सकते हैं। उदाहरण के लिए, मेरे पास एक छह-पक्षीय बक्से है जिसे एक कैसीनो ने हाथ और पैर से आगे बढ़ाया है, 1 की संभावना अधिक है, ¹⁄₂, 2, 3, 4, 5, 6 के उत्पादन की संभावना ¹⁄₁₀ है।

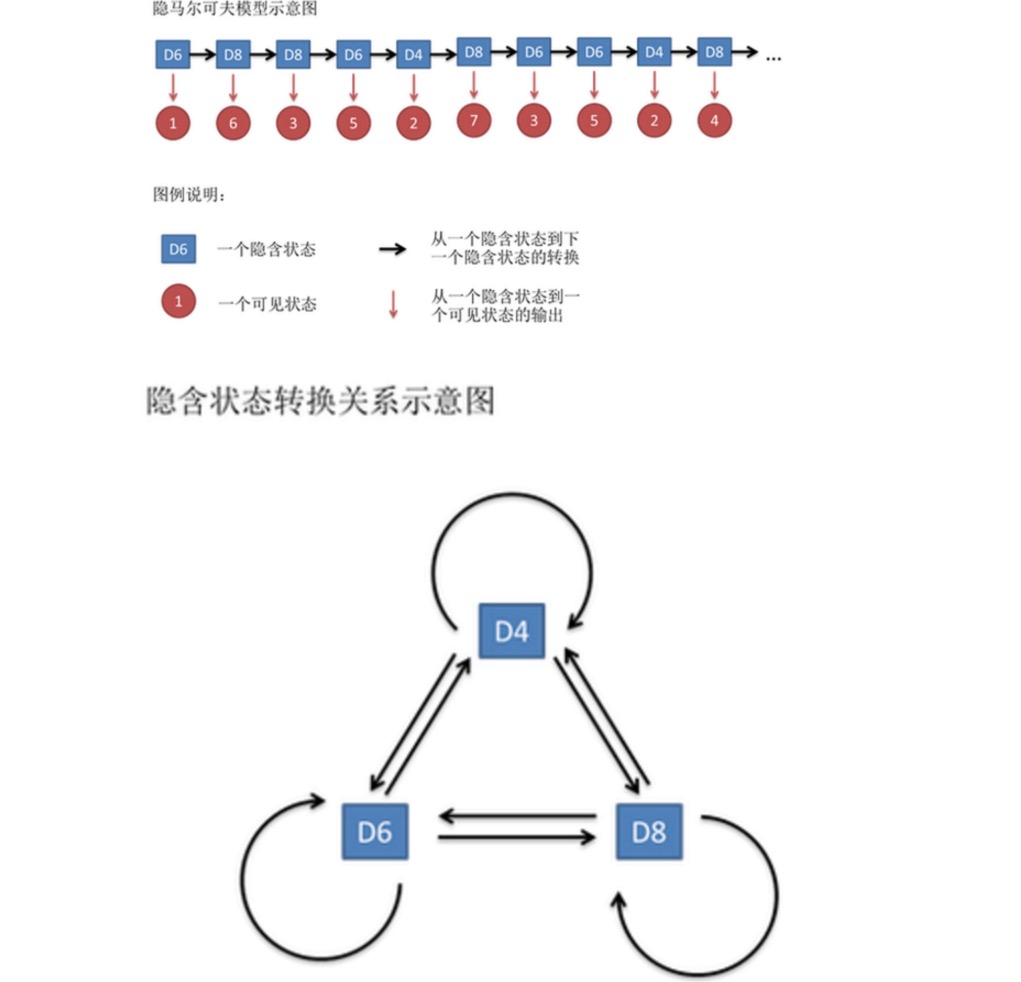
वास्तव में, एचएमएम के लिए, यदि सभी छिपी हुई स्थितियों के बीच रूपांतरण की संभावना और सभी छिपी हुई स्थितियों के बीच सभी दृश्यमान स्थितियों के बीच आउटपुट की संभावना को पहले से जाना जाता है, तो सिमुलेशन करना काफी आसान है। लेकिन जब एचएमएम मॉडल को लागू किया जाता है, तो अक्सर कुछ जानकारी गायब होती है। कभी-कभी आप जानते हैं कि कितने प्रकार के छल्ले हैं, प्रत्येक छल्ले क्या हैं, लेकिन आपको पता नहीं है कि छल्ले का अनुक्रम क्या है; कभी-कभी आप केवल छल्ले के परिणाम को कई बार देखते हैं, और बाकी के बारे में कुछ भी नहीं जानते हैं। यदि अनुप्रयोग एल्गोरिदम इन गायब जानकारी का अनुमान लगाने के लिए है, तो यह एक बहुत महत्वपूर्ण समस्या है।

एचएमएम मॉडल से संबंधित एल्गोरिदम को मुख्य रूप से तीन श्रेणियों में विभाजित किया गया है, जो तीन प्रकार की समस्याओं को हल करते हैंः

• मुझे पता है कि कितने प्रकार के छेद हैं (अवस्थितियों की संख्या), प्रत्येक छेद क्या है (परिवर्तन की संभावना), और प्रत्येक छेद के परिणाम के अनुसार (दृश्यमान राज्य श्रृंखला), मैं जानना चाहता हूं कि प्रत्येक बार किस प्रकार का छेद निकलता है (अवस्थितियों की श्रृंखला) ।

• मैं यह भी जानना चाहता हूँ कि कितने प्रकार के छेद हैं (अंतर्निहित अवस्थाओं की संख्या), प्रत्येक छेद क्या है (परिवर्तन की संभावना), और छेद से निकले परिणाम के आधार पर (दृश्यमान अवस्था श्रृंखला), मैं इस परिणाम को निकालने की संभावना जानना चाहता हूँ।

• मैं जानता हूँ कि कितने प्रकार के छेद हैं, मैं नहीं जानता कि प्रत्येक छेद क्या है, मैं नहीं जानता कि प्रत्येक छेद क्या है, मैं नहीं जानता कि प्रत्येक छेद क्या है, मैं नहीं जानता कि प्रत्येक छेद क्या है, मैं नहीं जानता कि प्रत्येक छेद क्या है, मैं नहीं जानता कि प्रत्येक छेद क्या है, मैं नहीं जानता कि प्रत्येक छेद क्या है, मैं नहीं जानता कि प्रत्येक छेद क्या है, मैं नहीं जानता कि प्रत्येक छेद क्या है, मैं नहीं जानता कि प्रत्येक छेद क्या है, मैं नहीं जानता कि प्रत्येक छेद क्या है, मैं नहीं जानता कि प्रत्येक छेद क्या है, मैं नहीं जानता कि प्रत्येक छेद क्या है, मैं नहीं जानता कि प्रत्येक छेद क्या है, मैं नहीं जानता कि प्रत्येक छेद क्या है, मैं नहीं जानता कि प्रत्येक छेद क्या है, मैं नहीं जानता कि प्रत्येक छेद क्या है।

  यदि हम शेयर बाजार में समस्या को हल करना चाहते हैं, तो हमें समस्या 1 और समस्या 3 को हल करने की आवश्यकता है, और अगले लेख में हम देखेंगे कि यह कैसे किया जाए।

मनीकोड से अनजान