सह-एकीकरण की सहज समझ

निर्देशः इस लेख का उद्देश्य एकीकरण की अवधारणा को एक दृश्य के रूप में प्रस्तुत करना है, ताकि आप इसके बुनियादी अर्थ, इस अवधारणा के लिए प्रेरित होने के साथ-साथ इसके सरल अनुप्रयोगों को समझ सकें।

• संश्लेषण

  यहाँ मैं केवल यह बताना चाहूँगा कि समरूपता की सहज परिभाषा में सख्त गणितीय संकेतों की परिभाषा और सख्त सूत्रों का अनुमान शामिल नहीं है।

  यदि आप रुचि रखते हैं, तो देखेंः विकिपीडिया Cointegration.

  क्यों एकजुट होना चाहिए?

  एकजुटता के बारे में बात करते हुए, हमें स्थिरता का उल्लेख करना होगा।

  सरल शब्दों में कहें तो, स्थिरता (stationarity) एक ऐसा गुण है जो समय के साथ स्थिर रहता है, और यह एक ऐसा गुण है जिसे हम डेटा के विश्लेषणात्मक भविष्यवाणियों को करते समय बहुत पसंद करते हैं। यदि समय-श्रृंखला डेटा का एक सेट स्थिर है, तो इसका मतलब है कि इसका औसत और विचलन अपरिवर्तित रहता है, जिससे हम आसानी से कुछ सांख्यिकीय तकनीकों का उपयोग कर सकते हैं। आइए पहले एक उदाहरण देखें कि स्थिर और गैर-स्थिर श्रृंखलाओं को देखने के लिए क्या दिखता है।

  

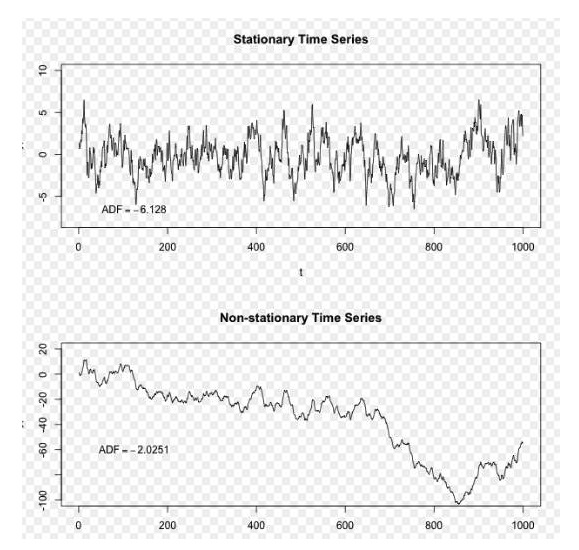
  तस्वीर स्रोतः विकिपीडिया

  उपरोक्त चित्र में, ऊपर की श्रेणी एक स्थिर श्रेणी है और हम देख सकते हैं कि यह हमेशा एक दीर्घकालिक औसत के आसपास घूमती रहती है, और नीचे की श्रेणी एक असंतुलित श्रेणी है और हम देख सकते हैं कि इसकी दीर्घकालिक औसत बदलती रहती है।

  एक उदाहरण के रूप में, यदि किसी परिसंपत्ति का मूल्य क्रम (या दो अनुक्रमों का अंतर) स्थिर है, तो जब यह अपने औसत मूल्य से विचलित हो जाता है, तो हम उम्मीद कर सकते हैं कि कीमत भविष्य में कुछ समय के लिए इस औसत मूल्य पर वापस आ जाएगी। हम इस गुण का उपयोग निवेश करने के लिए कर सकते हैं ताकि लाभ हो सके। मान लें कि एक स्टॉक का दीर्घकालिक औसत मूल्य 9 डॉलर है, और वर्तमान मूल्य 8 डॉलर है। यदि जांच की जाती है, तो हम मानते हैं कि इस स्टॉक का ऐतिहासिक क्रम स्थिर है, और यह स्थिरता बनाए रखने की संभावना है, तो हम केवल इस स्टॉक को खरीद सकते हैं और भविष्य में इसके मूल्य के लिए 9 डॉलर वापस आने का इंतजार कर सकते हैं, जिससे 1 डॉलर का लाभ होगा।

  यह स्टॉक की कीमतों का एक स्थिर क्रम हैः

  

  स्थिरता बहुत उपयोगी है, लेकिन वास्तविकता में, अधिकांश स्टॉक असमान हैं, तो क्या हम अभी भी लाभ के लिए स्थिरता के गुणों का उपयोग कर सकते हैं? जवाब हां है, तो सहसंयोजन (cointegration) खेल में है! यदि दो सेट अनुक्रम असमान हैं, लेकिन उनके रैखिक संयोजन से एक सुसंगत अनुक्रम प्राप्त किया जा सकता है, तो हम कह सकते हैं कि इन दो सेटों के समय अनुक्रम डेटा में सहसंयोजन गुण हैं, हम भी इस संयोजन के अनुक्रम पर सांख्यिकीय गुणों का उपयोग कर सकते हैं। लेकिन यह ध्यान देने योग्य है कि सहसंयोजन संबंध संबंध नहीं है।

  उदाहरण के लिए, यदि समय-श्रृंखला डेटा के दो सेटों में अंतर स्थिर है, तो हम इस अंतर की स्थिरता के आधार पर निवेश कर सकते हैं। जब दो शेयरों की कीमत में अंतर बहुत बड़ा होता है, तो हम स्थिरता के आधार पर मूल्य अंतर को समेटने की उम्मीद करते हैं, इसलिए कम कीमत वाले शेयरों को खरीदते हैं, उच्च कीमत वाले शेयरों को बेचते हैं, और कीमत की वापसी की प्रतीक्षा करते समय रिवर्स ऑपरेशन करते हैं ताकि लाभ हो सके।

  यह जोड़ी व्यापार की उत्पत्ति है। यह स्पष्ट है?

• स्थिरता और परीक्षण विधि

  सख्ती से, स्थिरता को दो प्रकार के रूप में वर्गीकृत किया जा सकता है, सख्ती से स्थिर और कमजोर स्थिर। सख्ती से स्थिरता का अर्थ है कि एक अनुक्रम में हमेशा एक अपरिवर्तित वितरण फ़ंक्शन होता है, जबकि कमजोर स्थिरता का अर्थ है कि अनुक्रम में अपरिवर्तित स्थिरांक की वर्णनात्मक सांख्यिकीय मात्रा होती है। सभी मजबूत स्थिरता अनुक्रम कमजोर स्थिरता गुणों को पूरा करते हैं, लेकिन इसके विपरीत नहीं है। हम आमतौर पर कहते हैं कि स्थिरता कमजोर स्थिरता है। समय अनुक्रम विश्लेषण में, हम आमतौर पर यूनिट रूट टेस्ट का उपयोग करके यह निर्धारित करते हैं कि कोई प्रक्रिया कमजोर स्थिर है या नहीं।

  

  उदाहरण के लिए एक ऐप

  सबसे पहले, यह ध्यान दिया जाना चाहिए कि एकजुटता संबंध संबंध नहीं है। हम कृत्रिम रूप से डेटा के दो सेटों का निर्माण करते हैं, इसलिए एकजुटता संबंधों को देखने के लिए।
  import numpy as np
  import pandas as pd
  import seaborn
  import statsmodels
  import matplotlib.pyplot as plt
  from statsmodels.tsa.stattools import coint

  संरचनात्मक डेटा

  सबसे पहले, हम डेटा के दो सेटों का निर्माण करते हैं, प्रत्येक डेटा 100 की लंबाई के साथ। पहला डेटा 100 है, इसके बाद एक डाउनट्रेंडिंग पॉइंट और एक मानक सामान्य वितरण है। दूसरा डेटा पहले डेटा के आधार पर 30 और एक अतिरिक्त मानक सामान्य वितरण है।

  

  

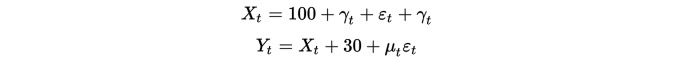
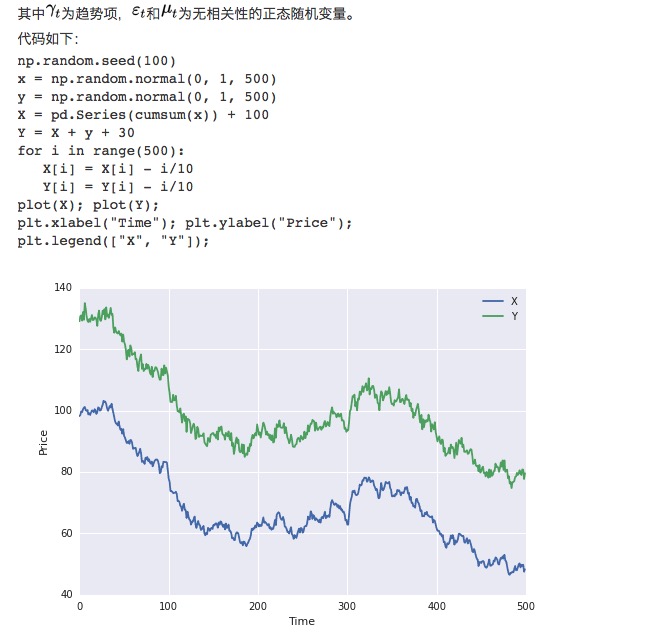
  स्पष्ट रूप से, डेटा के दोनों सेट असमान हैं, क्योंकि औसत समय के साथ बदलता है। लेकिन डेटा के दोनों सेट समरूपता से संबंधित हैं, क्योंकि उनके अंतर क्रम स्थिर हैंः

  plot(Y-X);
  plt.axhline((Y-X).mean(),color="red", linestyle="--");
  plt.xlabel("Time"); plt.ylabel("Price");
  plt.legend(["Y-X", "Mean"]);

  

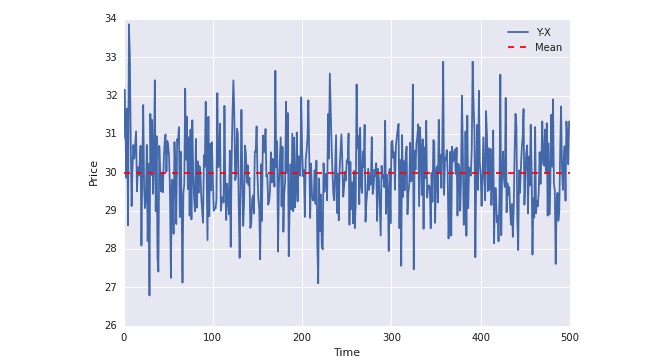
  उपरोक्त चित्र में, आप देख सकते हैं कि नीली रेखा हमेशा औसत के चारों ओर घूमती रहती है। और औसत समय के साथ नहीं बदलता है (वास्तव में, औसत समय के साथ नहीं बदलता है) ।

• निष्कर्ष

  यदि आप इसे पूरी तरह से गणितीय रूप से समझते हैं, तो यह जटिल है, और यह भविष्य की कक्षाओं में शामिल किया जाएगा। हम केवल एक सरल परिचय दे रहे हैं (स्तर -0) के स्तर पर, ताकि हम इसे वास्तविक अनुप्रयोगों के साथ बेहतर तरीके से जोड़ सकें।

और फिर, मैं आपको बताता हूं कि यह कैसे काम करता है, यह कैसे काम करता है।