बेयस, एक ऐसा व्यक्ति जो केवल शिक्षण सामग्री में रहता है

** जन्मजात बेयज़ के काम ने एक ओर यह साबित करना जारी रखा कि अनिश्चितता को मापा जा सकता है, और दूसरी ओर यह हमें एक तरीका प्रदान करता है कि हम अज्ञात संभावनाओं को निष्पादित कर सकते हैं, जो कि हमारे द्वारा प्राप्त जानकारी के निरंतर संशोधन के आधार पर उद्देश्य दुनिया के अनुभव के आधार पर है।

** यह एक बहुत ही अजीब बात है कि थॉमस बेयज़ जैसे व्यक्ति, जो पूरे वैज्ञानिक इतिहास में प्रसिद्ध हैं, उनके पास लिखने के लिए कुछ भी नहीं है। इस बात से पता चलता है कि बेयज़ वास्तव में बहुत ही नीच था (या, यह है कि, लाल नहीं) । दूसरी ओर, मेरे जैसे लेखकों के लिए बहुत बड़ी असुविधा है, क्योंकि वास्तव में हर कोई वैज्ञानिकों की अफवाहों को देखना पसंद करता है, जैसे कि गलत संगतता के साथ-साथ अहंकार, जैसे कि खिलौनों की उदासीनता के साथ-साथ आश्चर्यजनक है, और यह भी हो सकता है कि वे अध्ययन के लिए उत्सुक नहीं हैं, अन्यथा वे प्रतिभा की विशेषताओं को पूरी तरह से व्यक्त नहीं कर सकते हैं। **

• थॉमस बेयज़
  हालांकि, बेयज़ एक उबाऊ व्यक्ति था। वह एक गैर-प्रमुख पंथ का पुजारी था जो इंग्लैंड के ग्रामीण इलाकों में रहता था, और उसका काम शायद पूरे गांव को एक साथ डांस करने के लिए इकट्ठा करना था, नहीं, मस्जिद में, और कहा जाता है कि पूरे गांव ने उसे बहुत प्यार किया। केवल एक चीज जो थोड़ा पौराणिक लगती है वह यह है कि, कई किंवदंतियों की तरह, उन्होंने अपने जीवन में एक भी पुस्तक प्रकाशित नहीं की थी। निश्चित रूप से अधिकांश लोग जो पौराणिक नहीं हैं, वे भी हैं। बेयज़ ने संभावना के अध्ययन में शामिल होने का फैसला किया क्योंकि वह भगवान के अस्तित्व को साबित करना चाहता था, लेकिन अंतिम परिणामों और प्रभावों को देखते हुए, जो लोग चर्च के बारे में नहीं जानते थे, उन्हें लगता है कि वह एक विश्वासघात नहीं था।

  जब बेयिस की मृत्यु हुई, तो उन्होंने एक प्रचारक प्रिंस को अपने ग्रंथों की पांडुलिपि के अलावा 100 पाउंड छोड़ दिए। यह कहना कि प्रिंस एक अजीब आदमी था, आध्यात्मिक सभ्यता और भौतिक सभ्यता का निर्माण बेयिस को पता नहीं था कि वह कहाँ गया था। उन्होंने महसूस किया कि स्वतंत्र इच्छा ईश्वर द्वारा दी गई थी, और यह भी लिखा था कि अमेरिकी स्वतंत्रता भी ईश्वर की इच्छा थी, यह कहा जाता है कि फ्रैंकलिन और एडम्स स्मिथ उनके अच्छे दोस्त थे, इसके अलावा उन्होंने अपने खाली समय में बीमा कंपनियों के लिए शुल्क मॉडल बनाया, जो काफी व्यापक है।

  बेयज़ की मृत्यु के तीन साल बाद, प्रिंस ने बेयज़ के पत्राचार में मदद की। लेकिन इस पत्राचार के काल-निर्धारण के महत्व को अकादमिक समुदाय ने नजरअंदाज कर दिया, और दो दशक तक इंतजार किया। इस पत्राचार में, बेयज़ ने इस सवाल पर शोध करने का इरादा किया थाः यदि हम केवल एक घटना की घटनाओं की संख्या और घटनाओं की संख्या जानते हैं, तो अन्य जानकारी के अभाव में, हम इस घटना की संभावना की गणना कैसे करें?

  हम पिछले उदाहरण को याद करते हैं ((जोखिम की छोटी कहानी ((चौथा): डोनमोवर और देवताओं की वक्र)) । उदाहरण के लिए, हम 10,000 उत्पादों के एक बैच के लिए निकाले गए हैं और उनमें से 12 अपशिष्ट हैं, तो इस बैच के लिए अपशिष्ट दर 0.1% की संभावना कितनी है? वास्तविक जीवन के लिए, यह सवाल निस्संदेह हमारे लिए अधिक मूल्यवान है, क्योंकि हर व्यक्ति की चीजों की अवलोकन की सीमाएं हैं, हमें यह जानना होगा कि हम जो कुछ देखते हैं वह कितनी हद तक वास्तविकता को प्रतिबिंबित कर सकता है, जैसे कि अगर हम स्पर्श करते हैं, तो हम यह कैसे निर्धारित कर सकते हैं कि हम पूरी तरह से हाथी को छू रहे हैं या अपने बड़े भाई के पास जा रहे हैं जो मोटा है।

  बेयज़ का तरीका, वास्तव में, पुरानी जानकारी को नई जानकारी के साथ संशोधित करना है, जो संशोधन के आधार पर संभावनाओं की विश्वसनीयता को बढ़ाता है। यह किंवदंती में पूर्वगामी संभावना और पश्चगामी संभावना है। इस सवाल के लिए, बेयज़ ने अपने लेख में एक क्लासिक उदाहरण दिया हैः

  

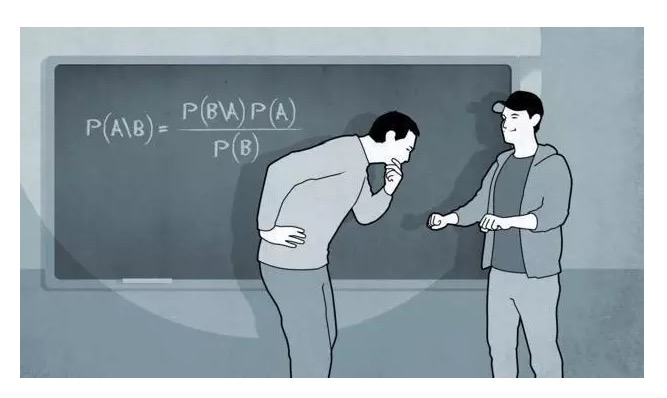
  यदि हम एक गेंद को टेनिस टेबल पर खेलते हैं और गेंद किसी भी स्थान पर रुक जाती है। फिर हम दूसरी गेंद को बार-बार खेलते हैं और इसे पहले गेंद के बाईं और दाईं ओर कितनी बार रोल किया गया है, इसकी गणना करते हैं। बेशक यहां आप उचित रूप से सवाल पूछ सकते हैं, क्योंकि हम टेनिस खेलने जा रहे हैं, तो दूसरी गेंद को पहले गेंद पर क्यों नहीं खेलते हैं, मुझे लगता है कि आपने यह सवाल बहुत अच्छा पूछा है, लेकिन मैं इसका जवाब नहीं देना चाहता। संक्षेप में, हम दूसरी गेंद के बाएं और दाईं ओर कितनी बार दिखाई देने के आधार पर सीधे पहले गेंद के रुकने की संभावना का अनुमान लगा सकते हैं।

  इस उदाहरण में, पहली गेंद के ठहरने की स्थिति के लिए सीधे दी गई संभावना पूर्वगामी है, जबकि दूसरी गेंद की स्थिति के आधार पर अनुमानित पहली गेंद के ठहरने की स्थिति को संशोधित करने की संभावना पश्चगामी है। अर्थात्, बेयज़ की विधि यह है कि हमारी समझ हमारी संज्ञानात्मक क्षमता की सीमाओं के अधीन है, इसलिए हमें लगातार अद्यतन जानकारी के साथ अपनी राय को संशोधित करने की आवश्यकता है। और दार्शनिक ऊंचाई तक पहुंचने के लिए, यह है कि दुनिया की उत्पत्ति शायद यादृच्छिक नहीं है, लेकिन हमारी क्षमता हमें ऐसी उत्पत्ति को पहचानने के लिए पर्याप्त नहीं है, इसलिए हम केवल अनुमान लगाने के लिए, या कहने के लिए, अनुमान लगाने के लिए पर्याप्त हैं।

  उपरोक्त वाक्य शायद अब तक का सबसे आक्रामक वाक्य है। आइए मान लें कि एक उदाहरण समझने में मदद करता हैः

  सिचुआन ने आपके शहर में दो मॉल खोले हैं, और नए मॉल में लोगों का आवागमन कुल आवागमन का 60% है, तो इस समय किसी भी ग्राहक के लिए सिचुआन के लिए, 60% संभावना है कि नए मॉल का ग्राहक है। यह पूर्वानुमान है। और पुराने मॉल की सुविधाएं प्रबंधन के लिए पुरानी हैं, कर्मचारियों का प्रशिक्षण स्तर भी कम है, और प्राप्त शिकायतों की दर नए मॉल की तुलना में दोगुनी है। इस समय यदि कोई व्यक्ति सिचुआन को शिकायत भेजता है, तो सिचुआन को किस मॉल के प्रबंधक को जिम्मेदार ठहराया जाना चाहिए?

  

  सबसे संक्षिप्त और समझदार उत्तर यह है कि सिचुआन सीधे उस व्यक्ति से पूछता है कि वह कहाँ है। बेशक वह व्यक्ति यह जवाब देगा कि आप अनुमान लगा सकते हैं ((बहुत खराब है), तो सिचुआन को कैसे अनुमान लगाना चाहिए कि अधिक सही संभावनाएं होंगी? यदि पूर्वानुमान के अनुसार, तो सिचुआन को नए मॉल के प्रबंधक को ढूंढना चाहिए, क्योंकि नए मॉल में लोगों का आवागमन पुराने मॉल की तुलना में अधिक है। लेकिन शिकायतों के संदर्भ में, नए मॉल में शिकायतों की संख्या कुल शिकायतों का केवल 1/3 है। तो अगर हम इस जानकारी का संदर्भ लेते हैं, तो हम पाएंगे कि नए मॉल में शिकायतों की संभावना 42.8% है और पुराने मॉल में शिकायतों की संभावना 57.2% है। यह परिणाम है, अर्थात्, बाद की संभावना, हमें बताती है कि सिचुआन को पुराने मॉल के प्रबंधक को ढूंढना चाहिए।

  जन्मजात बेयस अब लगभग सभी सांख्यिकी, कृत्रिम बुद्धिमत्ता, खेल सिद्धांत और आनुवंशिकी के पाठ्यपुस्तकों में दिखाई देते हैं, जिससे कई विश्वविद्यालय के अंतिम वर्ष के परीक्षार्थियों को जीवन भर परेशानी होती है। उनका काम एक तरफ यह साबित करना जारी रखता है कि अनिश्चितता एक रोमांचक विचार है जिसे आप माप सकते हैं, और दूसरी ओर, यह हमें एक तरीका प्रदान करता है कि आप अपने अनुभवों के आधार पर अज्ञात संभावनाओं का अनुमान लगा सकते हैं, जो हमें प्राप्त जानकारी के निरंतर संशोधन के परिणामस्वरूप प्राप्त होता है। यह विचार हमारे जोखिम प्रबंधन के उद्देश्यों और अभ्यास के साथ असंगत हैः एक गतिशील बाजार में, यदि अनिश्चितता मौजूद है, तो कोई भी परिणाम और निर्णय हमारे पास नवीनतम और सबसे व्यापक जानकारी पर निर्भर करता है, और इस तरह के तर्क को रोकना समान नहीं है।

चीन के क्वांटिटेटिव इन्वेस्टमेंट एसोसिएशन से साभार