वान मोवर और देवताओं की वक्रता

पिछले अंक में कहा गया था कि जब जैकब बर्नली की मृत्यु हुई, तब भी उन्होंने अपनी पुस्तक के बारे में अनुमान नहीं प्रकाशित किया था। उनकी पांडुलिपियों को व्यवस्थित करने का काम उनके भतीजे निकोलस बर्नली द्वितीय को सौंप दिया गया था। निकोलस ने चाचा की इच्छा पूरी करने के बाद, वास्तविक संभावनाओं के स्तर के विचलन के बारे में अध्ययन करना शुरू कर दिया था, जिसमें पहले से ही अवलोकनों की संख्या का निर्धारण किया गया था। शायद प्रतिभा को लगता था कि वह अपने आप को परेशान नहीं कर रहा था, इसलिए उन्होंने मॉर्फ को अध्ययन में शामिल होने के लिए आमंत्रित किया। मोइवर को कई स्थानों पर मोइवर के रूप में अनुवादित किया गया है, लेकिन उनकी छवि को देखने के बाद, मैं इस अनुवाद के पक्ष में नहीं हूं। यह निमंत्रण एक भविष्यवाणी के रूप में काम कर सकता था, लेकिन मोइवर ने इसे अस्वीकार कर दिया। और उन्होंने इसे अस्वीकार करने का कारण यह बताया कि उन्हें लगा कि उनके पास पर्याप्त ताकत नहीं है।

• डेमोवर डेमॉर्फ वास्तव में जेकब बर्नौली से केवल एक किशोरी थी, और उसका पूरा जीवन वास्तव में एक उपन्यास के रूप में वर्णित किया जा सकता था, जो कि द वेरेस्ट वर्ल्ड था। उस समय फ्रांस एक कैथोलिक देश था, और डेमॉर्फ एक प्रोटेस्टेंट था। बाद में फ्रांस के राजा लुई चौदह ने एक डिक्री जारी की, जिसमें देश के प्रोटेस्टेंटों को कमतर नागरिक घोषित किया गया था, बच्चों को प्रोटेस्टेंट धर्म में परिवर्तित होना पड़ा, जो कि फ्रांस में प्रोटेस्टेंट धर्म को एक संप्रदाय के रूप में स्थापित करने का एक तरीका था, और डेमॉर्फ ने दो साल जेल में बिताए। जेल से बाहर डेमॉर्फ की योजना इंग्लैंड में भागने की थी, लेकिन उन्हें अंततः शिक्षाविदों में कोई पद नहीं मिला, हालांकि वे न्यूटन के दोस्त थे, और 30 साल की उम्र में वे ब्रिटिश शाही परिवार के सदस्य थे। डेमॉर्फ ने गणितज्ञों और सलाहकारों पर भरोसा किया, और अपने दैनिक जीवन को बनाए रखने के लिए, उन्होंने कहा कि बुनियादी गणित का निर्माण करना, खेलना और बदनाम करना उनकी ऊर्जा का परिणाम था,

लेकिन फिर भी हम यहाँ जोर से पुकारते हैं, कि ड्यूमॉर्फ अमर रहे! 1711 में ड्यूमॉर्फ ने भाग्य के माप के बारे में एक मिथक प्रकाशित किया था, और अगर उस समय एक पुस्तक का एक आवरण होता, तो न्यूटन की सिफारिश निश्चित रूप से आवरण पर होतीः ड्यूमॉर्फ से पूछो, वह इस मामले में मुझसे अधिक जानता है।

दुर्भाग्यवश, उस समय ऐसा नहीं था, और इसलिए ड्यूमॉवर को बहुत अधिक करों के लिए अपने पैरों को पकड़ने का मौका नहीं मिला।

आपको याद होगा कि हमने पिछले लेख में जो समस्या दी थी, वह यह थी कि एक गड्ढे में 5000 पत्थरों के लिए हम 25,500 बार पकड़ कर अनुमान लगा सकते हैं कि कुल मिलाकर कितने पत्थर हैं। लेकिन आपको यह भी पता चल जाएगा कि 25,500 बार पकड़ना बहुत ज्यादा है, यह एक पत्थर को एक नंबर से बाहर फेंकने के बराबर है।

प्यूमॉवर ने अमूर्तगणित और पास्कल त्रिभुज का उपयोग करके समूह-नमूने की विधि अपनाई। उन्होंने माना कि हर बार 100 प्यूमॉवर को गड्ढे से बाहर निकाला जाता है, काले और सफेद प्यूमॉवर के अनुपात को नोट किया जाता है और उन्हें वापस रखा जाता है, और फिर वही निकाला जाता है। इस तरह से, प्यूमॉवर आपको पहले से बता सकता है कि आपके द्वारा दर्ज किए गए अनुपात वास्तविक अनुपात से अनुमानित विचलन हैं, और ये अनुपात उनके औसत के आसपास कैसे वितरित होते हैं।

क्या यह एक परिचित वाक्यांश है, या यह आपके मुंह में है, या आप इसे तुरंत नाम देना चाहते हैं? हाँ, यह सामान्य वितरण है जिसके साथ हम सभी परिचित हैं। सामान्य वितरण की वक्र एक बेलन की तरह होती है, जिसमें अधिकांश अवलोकन मूल्य केंद्र में एकत्रित होते हैं, सभी अवलोकन मूल्यों के औसत के करीब होते हैं, और फिर औसत से सममित रूप से दोनों ओर झुकाव करते हैं, और औसत के दोनों छोरों पर अवलोकन मूल्यों की संख्या समान होती है। शुरुआत में, वक्र तेज गति के तहत झुकाव होता है, और दोनों छोरों पर, इस तरह का झुकाव समतल हो जाता है, जिसका अर्थ है कि अवलोकन मूल्यों की संभावना उतनी ही कम होती है जितनी दूर औसत से होती है। कई वर्षों के बाद, किसी भी सांख्यिकीय पाठ्यपुस्तक में इस वक्र का वर्णन है और इसे मॉर्फिलियन सेंटर ऑफ लिमिट कहा जाता है।

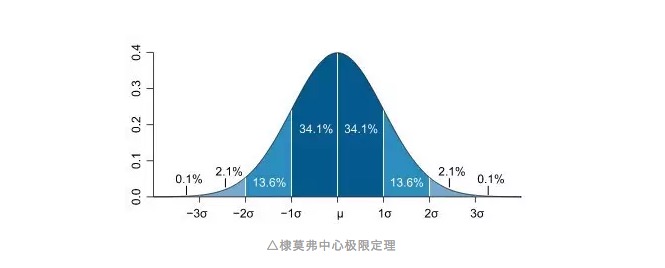
इस प्रकार हम मानक विचलन की अवधारणा को लागू कर सकते हैं, और वास्तव में, हमने इसे पहले ही सार्वजनिक संस्करण के अन्य लेखों में उल्लेख किया है। मानक विचलन वास्तव में औसत से विचलन की डिग्री को दर्शाता है, या हम इसे औसत से विचलन की इकाइयों के रूप में समझते हैं। एक सामान्य वितरण के लिए, हम 100 समूहों में से एक के लिए माउस के पत्थरों का अनुपात लेते हैं। लगभग 68% औसत के दो-पक्षीय मानक विचलन के भीतर आते हैं, जबकि दो मानक विचलन के दायरे में लगभग 95% अवलोकन शामिल हैं।

एक धार्मिक व्यक्ति के रूप में, डेमोवर ने घंटों की वक्रता को ईश्वर का उत्पाद माना। उनके अनुसार, इस तरह के माप से हम अनिश्चितता को दूर कर सकते हैं और सभी जोखिमों पर विजय प्राप्त कर सकते हैं, क्योंकि वक्र पर सभी संभावित घटनाओं और उनकी संभावनाओं का वर्णन किया गया है, शायद संयोग से तथाकथित विचलन पैदा हो सकते हैं, लेकिन समय के साथ, ये विचलन अब हमारे निष्कर्षों को प्रभावित नहीं करेंगे।

मोवर के शब्दों को हमारे पसंदीदा तरीके से समझें, निराशा कभी-कभी एक फोन नंबर है जिसे डायल नहीं किया जा सकता है, और कई बार कोशिश करें, और हमेशा जवाब दें . माध्यमिक विद्यालय में एक क्लासिक विषय भी है ((, मैं हमेशा माध्यमिक विद्यालय के विषय का उपयोग क्यों करता हूं)) उत्पाद उत्तीर्णता के बारे में . यदि उत्पादों के एक बैच के लिए, उद्योग के मानकों का मानना है कि अपशिष्ट की दर 0.1% से अधिक नहीं है, तो यह उत्तीर्ण है, इसका मतलब है कि हम 10,000 उत्पादों को यादृच्छिक रूप से चुनते हैं, जिनमें से यदि अपशिष्ट 10 से अधिक नहीं है, तो वे उत्तीर्ण हो गए हैं . लेकिन परिणाम यह है कि 10,000 में से 12 अंत में दिखाई देते हैं, यदि औसत पर उत्पाद की अपशिष्ट दर 0.1% है, तो वास्तव में हम मोवर के तरीके का उपयोग कर सकते हैं, 12 अपशिष्ट उत्पादों की संभावना क्या है .

लेकिन यह सवाल अक्सर हमारे लिए बहुत मायने नहीं रखता है। क्योंकि हम शायद यह नहीं जानते कि उत्पाद की औसत अपशिष्ट दर क्या होगी, और यदि औसत अपशिष्ट दर परीक्षण मानक से अधिक है, तो हमारे उत्पादों के एक बैच के पास होने की संभावना कितनी होगी? यदि 20,000 उत्पादों का परीक्षण किया जाता है, तो क्या 10,000 उत्पादों के परिणाम सीधे उपयोग में लाए जा सकते हैं? ये प्रश्न पोंटमोवर की वक्र के साथ व्याख्या करने के लिए बहुत मुश्किल लगते हैं। तो, एक बेयज़ का नाम जो सभी सांख्यिकी और जुआरी सिद्धांतों में दिखाई देगा, इसे कहा जाता है, और यह हमारे अगले संस्करण का विषय होगा।

चीन के क्वांटिटेटिव इन्वेस्टमेंट एसोसिएशन से साभार