पायथन नैवे बेयस अनुप्रयोग

बेयज़ के सिद्धांतों के अनुसार, एक साधारण बेयज़ वर्गीकरण प्राप्त किया जा सकता है यदि पूर्वानुमानित चर एक दूसरे से स्वतंत्र हैं। अधिक सरल शब्दों में, एक साधारण बेयज़ वर्गीकरणकर्ता वर्गीकरण की एक विशेषता को उस वर्गीकरण की अन्य विशेषताओं से असंबंधित मानता है। उदाहरण के लिए, यदि एक फल गोल और लाल है, और इसका व्यास लगभग 3 इंच है, तो यह फल एक सेब हो सकता है। भले ही ये विशेषताएं एक दूसरे पर निर्भर हों, या अन्य विशेषताओं पर निर्भर हों, लेकिन एक साधारण बेयज़ वर्गीकरणकर्ता इन विशेषताओं को स्वतंत्र रूप से मानता है, जिससे यह संकेत मिलता है कि फल एक सेब है।

• #### सरल बेयज़ मॉडल बनाने में आसान है और बड़े डेटासेट के लिए बहुत उपयोगी है। सरल होने के बावजूद, सरल बेयज़ प्रदर्शन बहुत जटिल वर्गीकरण विधियों से परे है।

बेयज़ के प्रमेय से P © = P (x) = P (x) = P (x) = P © = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (

और यहाँ,

P (c < c < dx) एक ज्ञात भविष्यवाणी चर (गुण) के आधार पर, वर्ग (लक्ष्य) के बाद की संभावना है P © वर्ग की पूर्वगामी संभावना है P ((xfin_Latnfin_Latnfin_Latnfin_Latnfin_Latnfin_Latn Mikä on todennäköisyys) on todennäköisyys, joka ennustaa muuttujan, jos se on tunnettu. P (x) पूर्वानुमानित चर की पूर्वगामी संभावना है उदाहरण: आइए इस अवधारणा को एक उदाहरण के साथ समझें। नीचे, मेरे पास मौसम के लिए एक प्रशिक्षण सेट है और इसके लिए एक लक्ष्य चर Play है। अब, हमें मौसम की स्थिति के आधार पर खिलाड़ियों को खेलने वाले और न खेलने वाले खिलाड़ियों के बीच वर्गीकृत करने की आवश्यकता है। आइए निम्नलिखित चरणों का पालन करें।

चरण 1: डेटासेट को एक आवृत्ति तालिका में बदलें

चरण 2: इस तरह की संभावनाओं के साथ एक समान तालिका का उपयोग करें जब ओवरकास्ट की संभावना 0.29 है, और खेल की संभावना 0.64 है।

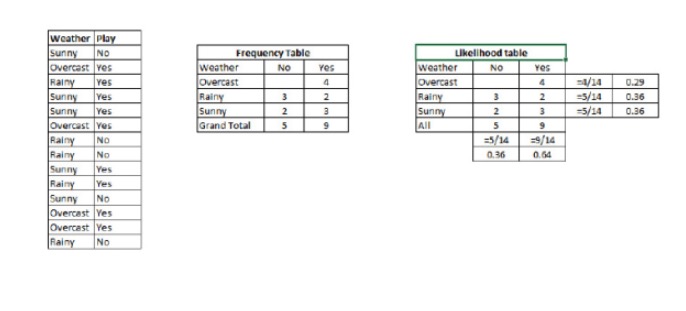
चरण 3: अब, सरल बेयज़ समीकरणों का उपयोग करके प्रत्येक श्रेणी के बाद की संभावना की गणना करें। सबसे बड़ी बाद की संभावना वाली श्रेणी भविष्यवाणी का परिणाम है।

प्रश्नः क्या यह कथन सही है कि अगर मौसम अच्छा है तो प्रतिभागी खेल सकते हैं?

हम इस समस्या को हल करने के लिए हमारे द्वारा चर्चा की गई विधि का उपयोग कर सकते हैं। तो P (खेलता है) = P (खेलता है) * P (खेलता है) / P (खेलता है)

हमारे पास P है ³⁄₉ = 0.33, P है ⁵⁄₁₄ = 0.36, P है ⁹⁄₁₄ = 0.64.

अब, P (खुश) = 0.33 * 0.64 / 0.36 = 0.60, और अधिक संभावना है.

सरल बेयज़ एक समान विधि का उपयोग करता है जो विभिन्न श्रेणियों की संभावनाओं को अलग-अलग विशेषताओं के आधार पर भविष्यवाणी करता है। यह एल्गोरिथ्म आमतौर पर पाठ वर्गीकरण के साथ-साथ कई श्रेणियों से संबंधित समस्याओं के लिए उपयोग किया जाता है।

• #### पायथन कोड:

  #Import Library
  from sklearn.naive_bayes import GaussianNB
  　　
  #Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset

Create SVM classification object model = GaussianNB()

there is other distribution for multinomial classes like Bernoulli Naive Bayes, Refer link

Train the model using the training sets and check score

model.fit(X, y) #Predict Output predicted= model.predict(x_test)