लेख में मुख्य रूप से उच्च आवृत्ति ट्रेडिंग रणनीतियों पर चर्चा की गई है, तथा संचयी मात्रा मॉडलिंग और मूल्य झटकों पर ध्यान केंद्रित किया गया है। यह शोधपत्र कीमतों पर एकल लेनदेन, निश्चित अंतराल मूल्य झटकों और लेनदेन मात्रा के प्रभाव का विश्लेषण करके एक प्रारंभिक इष्टतम ऑर्डर प्लेसमेंट मॉडल का प्रस्ताव करता है। यह मॉडल मात्रा और मूल्य झटकों की समझ के आधार पर इष्टतम ट्रेडिंग स्थिति खोजने का प्रयास करता है। मॉडल की मान्यताओं पर गहराई से चर्चा की गई है, तथा वास्तविक और मॉडल-पूर्वानुमानित अपेक्षित रिटर्न की तुलना करके इष्टतम ऑर्डर प्लेसमेंट का प्रारंभिक आकलन किया गया है।

संचयी वॉल्यूम मॉडलिंग

पिछले लेख में एकल लेनदेन की मात्रा के एक निश्चित मान से अधिक होने की संभाव्यता अभिव्यक्ति प्राप्त की गई थी:

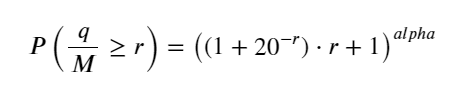
हम एक समयावधि में ट्रेडिंग वॉल्यूम के वितरण के बारे में भी चिंतित हैं, जो सहज रूप से प्रत्येक लेनदेन की मात्रा और ऑर्डर आवृत्ति से संबंधित होना चाहिए। इसके बाद, डेटा को निश्चित अंतराल पर संसाधित किया जाता है। इसका वितरण ऊपर बताए अनुसार दर्शाइए।

from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

trades = pd.read_csv('HOOKUSDT-aggTrades-2023-01-27.csv')
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
    'agg_trade_id': 'last',
    'price': 'last',
    'quantity': 'sum',
    'first_trade_id': 'first',
    'last_trade_id': 'last',
    'is_buyer_maker': 'last',
    'date': 'last',
    'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
buy_trades.index = buy_trades['date']

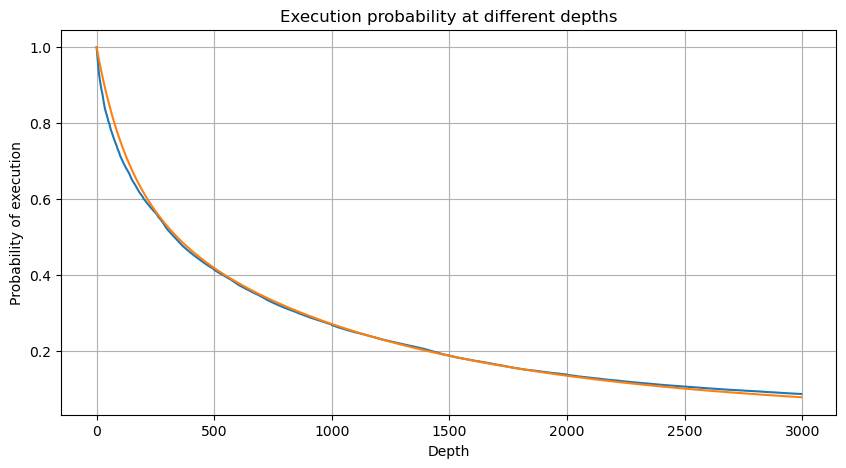
हर 1 सेकंड में ट्रांजेक्शन वॉल्यूम को मर्ज करें, उस हिस्से को हटा दें जहां कोई ट्रांजेक्शन नहीं हुआ है, और फिट करने के लिए ऊपर दिए गए सिंगल ट्रांजेक्शन के वितरण का उपयोग करें। यह देखा जा सकता है कि परिणाम बेहतर है। यदि 1 सेकंड के भीतर सभी ट्रांजेक्शन को सिंगल ट्रांजेक्शन माना जाता है, तो यह समस्या बन जाती है यह एक हल हो चुकी समस्या बन गई है। हालाँकि, जब चक्र लंबा हो जाता है (लेनदेन आवृत्ति के सापेक्ष), तो त्रुटि बढ़ जाती है, और शोध में पाया गया है कि यह त्रुटि पिछले पेरेटो वितरण सुधार अवधि के कारण होती है। इसका मतलब यह है कि जैसे-जैसे चक्र लंबा होता जाता है और इसमें अधिक व्यक्तिगत लेन-देन शामिल होते हैं, कई लेन-देन का संयोजन पेरेटो वितरण के करीब पहुंच जाता है। इस मामले में, सुधार अवधि को हटा दिया जाना चाहिए।

df_resampled = buy_trades['quantity'].resample('1S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]

buy_trades

	agg_trade_id	price	quantity	first_trade_id	last_trade_id	is_buyer_maker	date	transact_time	interval	diff
2023-01-27 00:00:00.161	1138369	2.901	54.3	3806199	3806201	False	2023-01-27 00:00:00.161	1674777600161	NaN	0.001
2023-01-27 00:00:04.140	1138370	2.901	291.3	3806202	3806203	False	2023-01-27 00:00:04.140	1674777604140	3979.0	0.000
2023-01-27 00:00:04.339	1138373	2.902	55.1	3806205	3806207	False	2023-01-27 00:00:04.339	1674777604339	199.0	0.001
2023-01-27 00:00:04.772	1138374	2.902	1032.7	3806208	3806223	False	2023-01-27 00:00:04.772	1674777604772	433.0	0.000
2023-01-27 00:00:05.562	1138375	2.901	3.5	3806224	3806224	False	2023-01-27 00:00:05.562	1674777605562	790.0	0.000
…	…	…	…	…	…	…	…	…	…	…
2023-01-27 23:59:57.739	1544370	3.572	394.8	5074645	5074651	False	2023-01-27 23:59:57.739	1674863997739	1224.0	0.002
2023-01-27 23:59:57.902	1544372	3.573	177.6	5074652	5074655	False	2023-01-27 23:59:57.902	1674863997902	163.0	0.001
2023-01-27 23:59:58.107	1544373	3.573	139.8	5074656	5074656	False	2023-01-27 23:59:58.107	1674863998107	205.0	0.000
2023-01-27 23:59:58.302	1544374	3.573	60.5	5074657	5074657	False	2023-01-27 23:59:58.302	1674863998302	195.0	0.000
2023-01-27 23:59:59.894	1544376	3.571	12.1	5074662	5074664	False	2023-01-27 23:59:59.894	1674863999894	1592.0	0.000

#1s内的累计分布
depths = np.array(range(0, 3000, 5))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])

plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)

df_resampled = buy_trades['quantity'].resample('30S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 12000, 20))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2)
probabilities_s_2 = np.array([(depth/mean+1)**alpha for depth in depths]) # 无修正

plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities,label='Probabilities (True)')
plt.plot(depths, probabilities_s, label='Probabilities (Simulation 1)')
plt.plot(depths, probabilities_s_2, label='Probabilities (Simulation 2)')
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.legend() 
plt.grid(True)

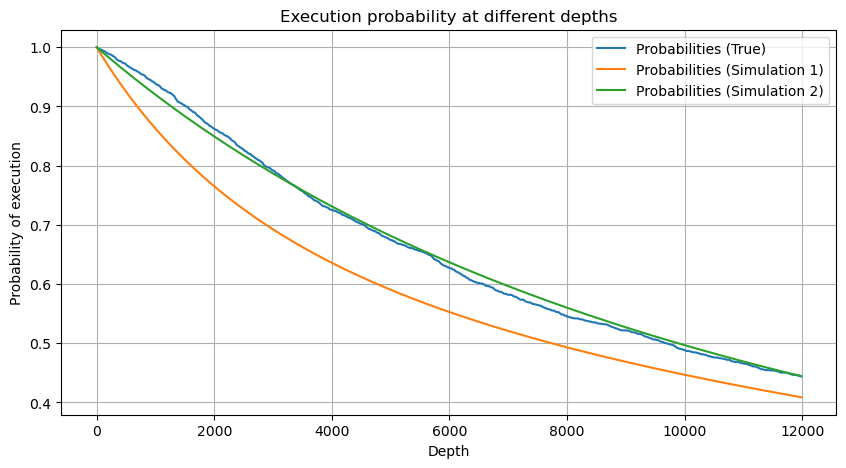
अब हमने विभिन्न समयों पर संचित ट्रेडिंग वॉल्यूम के वितरण के लिए एक सामान्य सूत्र का सारांश तैयार किया है, तथा इसे फिट करने के लिए एकल लेनदेन के वितरण का उपयोग किया है, तथा प्रत्येक बार उन्हें अलग से गिनने की आवश्यकता नहीं है। यहां हम प्रक्रिया को छोड़ देते हैं और सीधे सूत्र देते हैं:

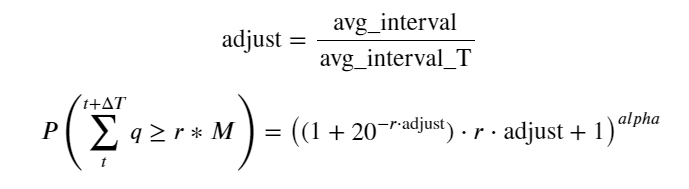
उनमें से, avg_interval एकल लेनदेन के बीच औसत अंतराल का प्रतिनिधित्व करता है, और avg_interval_T उन अंतरालों के औसत अंतराल का प्रतिनिधित्व करता है जिनका अनुमान लगाने की आवश्यकता है। यह थोड़ा भ्रमित करने वाला है। यदि हम 1 सेकंड के लेनदेन समय का अनुमान लगाना चाहते हैं, तो हमें 1 सेकंड के भीतर लेनदेन वाले घटनाओं के बीच औसत अंतराल की गणना करनी होगी। यदि किसी ऑर्डर के आने की संभावना पॉइसन वितरण के अनुरूप है, तो इसका सीधे अनुमान लगाना संभव होना चाहिए, लेकिन वास्तविक विचलन बड़ा है, इसलिए मैं इसे यहां स्पष्ट नहीं करूंगा।

ध्यान दें कि एक निश्चित अंतराल के भीतर वॉल्यूम के एक निश्चित मूल्य से अधिक होने की संभावना गहराई में उस स्थिति में लेनदेन की वास्तविक संभावना से काफी भिन्न होनी चाहिए, क्योंकि प्रतीक्षा समय जितना लंबा होगा, ऑर्डर बुक होने की संभावना उतनी ही अधिक होगी गहराई में परिवर्तन होता है, इसलिए डेटा अपडेट होने पर समान गहराई की स्थिति में लेनदेन की संभावना वास्तविक समय में बदल जाती है।

df_resampled = buy_trades['quantity'].resample('2S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 6500, 10))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = buy_trades['quantity'].mean()
adjust = buy_trades['interval'].mean() / 2620
alpha = np.log(np.mean(buy_trades['quantity'] > mean))/0.7178397931503168
probabilities_s = np.array([((1+20**(-depth*adjust/mean))*depth*adjust/mean+1)**(alpha) for depth in depths])

plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)

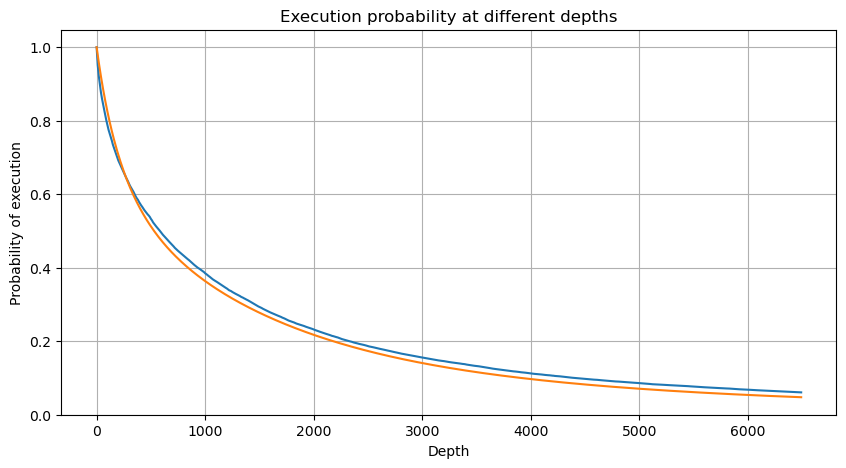
एकल लेनदेन मूल्य प्रभाव

लेन-देन संबंधी डेटा एक खजाना है, और अभी भी बहुत सारा डेटा निकाला जाना बाकी है। हमें कीमतों पर ऑर्डर के प्रभाव पर बारीकी से ध्यान देना चाहिए, जो रणनीति में लंबित ऑर्डर की नियुक्ति को प्रभावित करता है। इसी तरह, transact_time कुल डेटा के आधार पर, अंतिम कीमत और पहली कीमत के बीच अंतर की गणना करें। यदि केवल एक ऑर्डर है, तो अंतर 0 है। अजीब बात यह है कि अभी भी कुछ संख्या में डेटा परिणाम नकारात्मक हैं। यह डेटा व्यवस्था के क्रम में एक समस्या होनी चाहिए, इसलिए मैं यहाँ इस पर बात नहीं करूँगा।

परिणाम दर्शाते हैं कि बिना प्रभाव वाले लोगों का अनुपात 77% जितना अधिक है, 1 टिक का अनुपात 16.5% है, 2 टिक का अनुपात 3.7% है, 3 टिक का अनुपात 1.2% है, और 4 से अधिक टिक का अनुपात 1% से कम है . यह मूलतः घातांकीय फ़ंक्शन की विशेषताओं के अनुरूप है, लेकिन फिटिंग सटीक नहीं है।

संबंधित मूल्य अंतर का कारण बनने वाले लेनदेन की मात्रा की गणना की गई, और बहुत बड़े प्रभाव के कारण होने वाली विकृति को हटा दिया गया। यह मूल रूप से रैखिक संबंध के अनुरूप है, और लगभग हर 1,000 वॉल्यूम 1 टिक के मूल्य में उतार-चढ़ाव का कारण बनता है। इसे ऐसे भी समझा जा सकता है कि प्रत्येक मूल्य के निकट लंबित ऑर्डरों की औसत संख्या लगभग 1,000 है।

diff_df = trades[trades['is_buyer_maker']==False].groupby('transact_time')['price'].agg(lambda x: abs(round(x.iloc[-1] - x.iloc[0],3)) if len(x) > 1 else 0)
buy_trades['diff'] = buy_trades['transact_time'].map(diff_df)

diff_counts = buy_trades['diff'].value_counts()
diff_counts[diff_counts>10]/diff_counts.sum()

0.000    0.769965
0.001    0.165527
0.002    0.037826
0.003    0.012546
0.004    0.005986
0.005    0.003173
0.006    0.001964
0.007    0.001036
0.008    0.000795
0.009    0.000474
0.010    0.000227
0.011    0.000187
0.012    0.000087
0.013    0.000080
Name: diff, dtype: float64

diff_group = buy_trades.groupby('diff').agg({
    'quantity': 'mean',
    'diff': 'last',
})

diff_group['quantity'][diff_group['diff']>0][diff_group['diff']<0.01].plot(figsize=(10,5),grid=True);

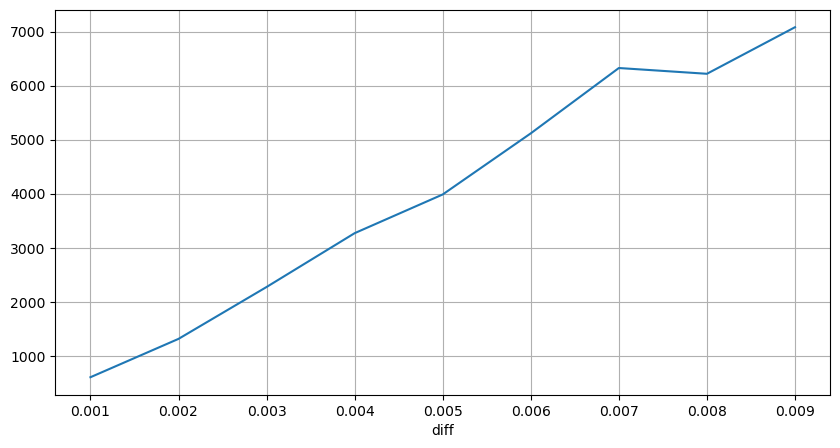
नियमित अंतराल पर मूल्य में उतार-चढ़ाव

2 सेकंड के भीतर कीमत के प्रभाव की गणना करें। यहाँ अंतर यह है कि नकारात्मक मूल्य होंगे। बेशक, चूँकि यहाँ केवल खरीद ऑर्डर गिने जाते हैं, इसलिए सममित स्थिति एक टिक बड़ी होगी। ट्रेडिंग वॉल्यूम और प्रभाव के बीच संबंध का निरीक्षण करना जारी रखें, और केवल 0 से अधिक परिणामों की गणना करें। निष्कर्ष एकल ऑर्डर के समान है, जो एक अनुमानित रैखिक संबंध भी है। प्रत्येक टिक के लिए लगभग 2000 वॉल्यूम की आवश्यकता होती है।

df_resampled = buy_trades.resample('2S').agg({ 
    'price': ['first', 'last', 'count'],
    'quantity': 'sum'
})
df_resampled['price_diff'] = round(df_resampled[('price', 'last')] - df_resampled[('price', 'first')],3)
df_resampled['price_diff'] = df_resampled['price_diff'].fillna(0)
result_df_raw = pd.DataFrame({
    'price_diff': df_resampled['price_diff'],
    'quantity_sum': df_resampled[('quantity', 'sum')],
    'data_count': df_resampled[('price', 'count')]
})
result_df = result_df_raw[result_df_raw['price_diff'] != 0]

result_df['price_diff'][abs(result_df['price_diff'])<0.016].value_counts().sort_index().plot.bar(figsize=(10,5));

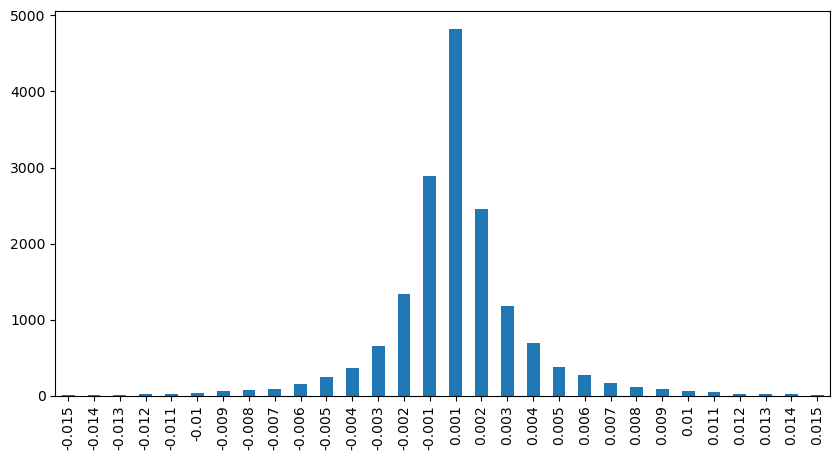
result_df['price_diff'].value_counts()[result_df['price_diff'].value_counts()>30]

 0.001    7176
-0.001    3665
 0.002    3069
-0.002    1536
 0.003    1260
 0.004     692
-0.003     608
 0.005     391
-0.004     322
 0.006     259
-0.005     192
 0.007     146
-0.006     112
 0.008      82
 0.009      75
-0.007      75
-0.008      65
 0.010      51
 0.011      41
-0.010      31
Name: price_diff, dtype: int64

diff_group = result_df.groupby('price_diff').agg({ 'quantity_sum': 'mean'})

diff_group[(diff_group.index>0) & (diff_group.index<0.015)].plot(figsize=(10,5),grid=True);

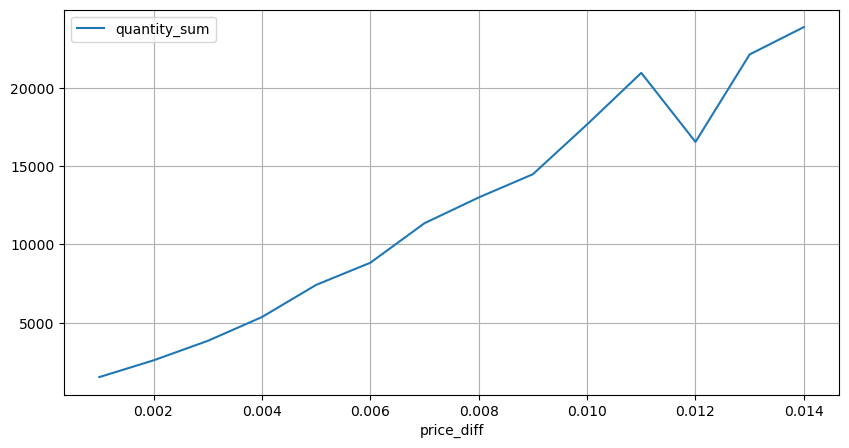
मात्रा का मूल्य प्रभाव

टिक परिवर्तन के लिए आवश्यक आयतन की गणना पहले की गई थी, लेकिन यह सटीक नहीं है क्योंकि यह इस धारणा पर आधारित है कि प्रभाव पहले ही घटित हो चुका है। अब आइए ट्रेडिंग वॉल्यूम के कारण मूल्य पर पड़ने वाले प्रभाव पर नजर डालें।

यहां डेटा को 1 सेकंड पर नमूना लिया जाता है, जिसमें 100 मात्राएं 1 चरण के रूप में होती हैं, और इस मात्रा सीमा के भीतर मूल्य परिवर्तन की गणना की जाती है। कुछ मूल्यवान निष्कर्ष निकाले गए:

1. जब खरीद मात्रा 500 से नीचे होती है, तो अपेक्षित मूल्य परिवर्तन नीचे होता है, जो कि अपेक्षित है क्योंकि मूल्य को प्रभावित करने वाले विक्रय आदेश भी होते हैं।
2. जब ट्रेडिंग वॉल्यूम कम होता है, तो यह एक रैखिक संबंध का अनुसरण करता है, अर्थात, ट्रेडिंग वॉल्यूम जितना अधिक होता है, कीमत में उतनी ही अधिक वृद्धि होती है।
3. खरीद ऑर्डर वॉल्यूम जितना बड़ा होगा, कीमत में बदलाव उतना ही अधिक होगा, जो अक्सर कीमत में एक ब्रेकथ्रू को दर्शाता है। ब्रेकथ्रू के बाद, कीमत वापस आ सकती है। निश्चित अंतराल पर सैंपलिंग के साथ, डेटा अस्थिर है।
4. स्कैटर प्लॉट के ऊपरी भाग पर ध्यान दिया जाना चाहिए, अर्थात वह भाग जहां वॉल्यूम मूल्य वृद्धि के अनुरूप होता है।
5. केवल इस ट्रेडिंग जोड़ी के लिए, मात्रा और मूल्य परिवर्तन के बीच संबंध का एक मोटा संस्करण दिया गया है:

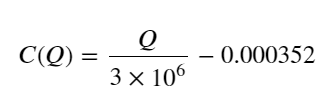
उनमें से, “सी” मूल्य में परिवर्तन का प्रतिनिधित्व करता है और “क्यू” खरीद आदेश मात्रा का प्रतिनिधित्व करता है।

df_resampled = buy_trades.resample('1S').agg({ 
    'price': ['first', 'last', 'count'],
    'quantity': 'sum'
})
df_resampled['price_diff'] = round(df_resampled[('price', 'last')] - df_resampled[('price', 'first')],3)
df_resampled['price_diff'] = df_resampled['price_diff'].fillna(0)
result_df_raw = pd.DataFrame({
    'price_diff': df_resampled['price_diff'],
    'quantity_sum': df_resampled[('quantity', 'sum')],
    'data_count': df_resampled[('price', 'count')]
})
result_df = result_df_raw[result_df_raw['price_diff'] != 0]

df = result_df.copy()
bins = np.arange(0, 30000, 100)  # 
labels = [f'{i}-{i+100-1}' for i in bins[:-1]]  
df.loc[:, 'quantity_group'] = pd.cut(df['quantity_sum'], bins=bins, labels=labels)
grouped = df.groupby('quantity_group')['price_diff'].mean()

grouped_df = pd.DataFrame(grouped).reset_index()
grouped_df['quantity_group_center'] = grouped_df['quantity_group'].apply(lambda x: (float(x.split('-')[0]) + float(x.split('-')[1])) / 2)

plt.figure(figsize=(10,5))
plt.scatter(grouped_df['quantity_group_center'], grouped_df['price_diff'],s=10)
plt.plot(grouped_df['quantity_group_center'], np.array(grouped_df['quantity_group_center'].values)/2e6-0.000352,color='red')
plt.xlabel('quantity_group_center')
plt.ylabel('average price_diff')
plt.title('Scatter plot of average price_diff by quantity_group')
plt.grid(True)

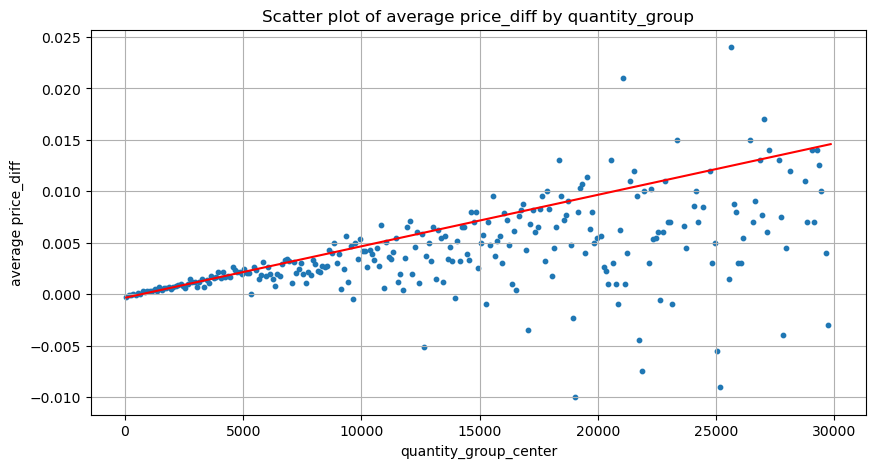
grouped_df.head(10)

	quantity_group	price_diff	quantity_group_center
0	0-199	-0.000302	99.5
1	100-299	-0.000124	199.5
2	200-399	-0.000068	299.5
3	300-499	-0.000017	399.5
4	400-599	-0.000048	499.5
5	500-699	0.000098	599.5
6	600-799	0.000006	699.5
7	700-899	0.000261	799.5
8	800-999	0.000186	899.5
9	900-1099	0.000299	999.5

प्रारंभिक इष्टतम ऑर्डर स्थिति

ट्रेडिंग वॉल्यूम के मॉडलिंग और मूल्य प्रभाव के अनुरूप ट्रेडिंग वॉल्यूम के एक मोटे मॉडल के साथ, ऐसा लगता है कि इष्टतम ऑर्डर स्थिति की गणना की जा सकती है। आइये कुछ धारणाएं बनाएं और एक गैर-जिम्मेदार इष्टतम मूल्य स्थिति दें।

1. मान लीजिए कि आघात के बाद कीमत अपने मूल मूल्य पर वापस आ जाती है (यह निश्चित रूप से असंभव है और आघात के बाद मूल्य में हुए परिवर्तनों का पुनः विश्लेषण आवश्यक है)
2. मान लें कि इस अवधि के दौरान ट्रेडिंग वॉल्यूम और ऑर्डर आवृत्ति का वितरण पूर्व निर्धारित आवश्यकताओं को पूरा करता है (यह भी गलत है, क्योंकि अनुमान के लिए एक दिन का मूल्य उपयोग किया जाता है, और लेनदेन में स्पष्ट क्लस्टरिंग होती है)।
3. मान लें कि सिमुलेशन समय के दौरान केवल एक विक्रय आदेश होता है और फिर स्थिति बंद हो जाती है।
4. यह मानते हुए कि ऑर्डर निष्पादित होने के बाद, कीमत को बढ़ाने के लिए अन्य खरीद ऑर्डर जारी हैं, खासकर जब वॉल्यूम बहुत कम है। इस प्रभाव को यहाँ अनदेखा किया जाता है और यह मान लिया जाता है कि यह वापस आ जाएगा।

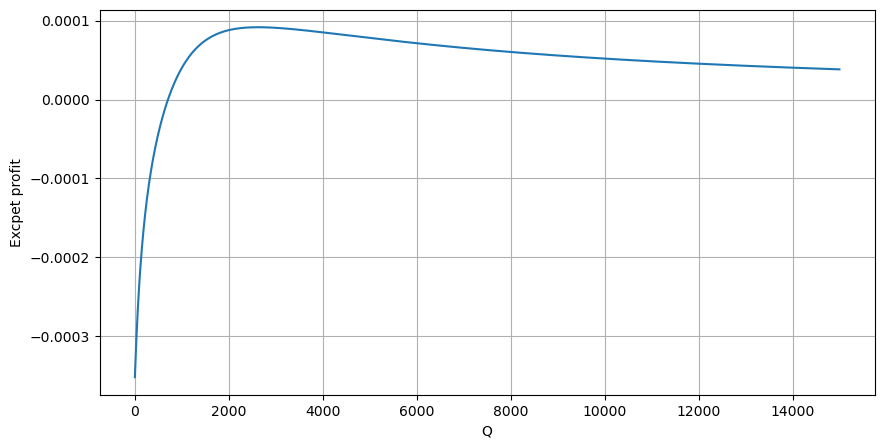
सबसे पहले, एक सरल अपेक्षित प्रतिफल लिखें, अर्थात, 1 सेकंड के भीतर संचयी खरीद आदेश Q से अधिक होने की संभावना, जिसे अपेक्षित प्रतिफल दर (अर्थात, प्रभाव मूल्य) से गुणा किया जाता है:

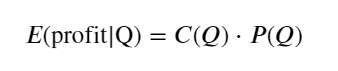
ग्राफ के अनुसार, अपेक्षित रिटर्न अधिकतम 2500 के आसपास है, जो औसत ट्रेडिंग वॉल्यूम का लगभग 2.5 गुना है। इसका मतलब यह है कि विक्रय आदेश 2500 पर रखा जाना चाहिए। इस बात पर पुनः जोर दिया जाना चाहिए कि क्षैतिज अक्ष 1 सेकंड के भीतर ट्रेडिंग वॉल्यूम को दर्शाता है और इसे केवल गहराई की स्थिति के साथ नहीं जोड़ा जा सकता है। और यह ऐसे समय में है जब अभी भी बहुत महत्वपूर्ण गहन डेटा का अभाव है, और यह केवल ट्रेडों पर आधारित अटकलों पर आधारित है।

संक्षेप

यह पाया गया है कि विभिन्न समय अंतरालों पर मात्रा वितरण, एकल लेनदेन के मात्रा वितरण का एक सरल मापन है। हमने मूल्य झटकों और लेनदेन की संभावना के आधार पर एक सरल अपेक्षित रिटर्न मॉडल भी बनाया है। इस मॉडल के परिणाम हमारी अपेक्षाओं के अनुरूप हैं। यदि बिक्री ऑर्डर की मात्रा कम है, तो यह मूल्य में गिरावट का संकेत देता है। एक निश्चित मात्रा में वॉल्यूम की आवश्यकता होती है लाभ मार्जिन है, और लेन-देन की मात्रा जितनी बड़ी होगी, लाभ मार्जिन उतना ही अधिक होगा। संभावना जितनी बड़ी होगी, यह उतना ही कम होगा। बीच में एक इष्टतम आकार है, जो ऑर्डर प्लेसमेंट की स्थिति भी है जिसे रणनीति तलाश रही है। बेशक, यह मॉडल अभी भी बहुत सरल है। अगले लेख में, मैं इस पर गहराई से चर्चा जारी रखूंगा।

#1s内的累计分布
df_resampled = buy_trades['quantity'].resample('1S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]

depths = np.array(range(0, 15000, 10))
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
profit_s = np.array([depth/2e6-0.000352 for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities_s*profit_s)
plt.xlabel('Q')
plt.ylabel('Excpet profit')
plt.grid(True)