उच्च आवृत्ति ट्रेडिंग रणनीतियों पर विचार (3)
 0
0
 2664
2664

पिछले लेख में, मैंने संचयी ट्रेडिंग वॉल्यूम का मॉडल बनाने का तरीका बताया था और मूल्य आघात परिघटना का संक्षेप में विश्लेषण किया था। यह आलेख ट्रेड ऑर्डर डेटा का विश्लेषण जारी रखेगा। पिछले दो दिनों में, YGG ने Binance U-आधारित अनुबंध लॉन्च किए, और कीमत में बहुत उतार-चढ़ाव आया, और एक समय पर ट्रेडिंग वॉल्यूम BTC से भी अधिक हो गया। आइए आज इसका विश्लेषण करें।
आदेश समय अंतराल
सामान्य तौर पर, यह माना जाता है कि ऑर्डर आने का समय पॉइसन प्रक्रिया का अनुसरण करता है। यहाँ एक लेख है जो परिचय देता हैपॉइसन प्रक्रिया . मैं इसे नीचे प्रदर्शित करूंगा।
5 अगस्त को aggTrades डाउनलोड करें, कुल 1,931,193 ट्रेड हैं, जो काफी अतिशयोक्तिपूर्ण है। सबसे पहले, आइए खरीद आदेशों के वितरण पर एक नज़र डालें। हम देख सकते हैं कि लगभग 100ms और 500ms पर एक असमान स्थानीय शिखर है। यह आइसबर्ग द्वारा सौंपे गए रोबोट द्वारा रखे गए अनुसूचित आदेशों के कारण होना चाहिए। यह भी एक हो सकता है उस दिन बाजार की स्थिति असामान्य होने के कारणों की चर्चा कीजिए।
पॉइसन वितरण का संभाव्यता द्रव्यमान फ़ंक्शन (पीएमएफ) इस प्रकार दिया गया है:
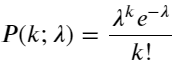
में:
- k उन घटनाओं की संख्या है जिनमें हमारी रुचि है।
- λ प्रति इकाई समय (या इकाई स्थान) में घटनाओं की औसत घटना दर है।
- P(k; λ) ठीक k घटनाओं के घटित होने की संभावना है, बशर्ते कि औसत घटना दर λ दी गई हो।
पॉइसन प्रक्रिया में, घटनाओं के बीच का समय अंतराल एक चरघातांकी वितरण का अनुसरण करता है। चरघातांकी वितरण का संभाव्यता घनत्व फ़ंक्शन (पीडीएफ) इस प्रकार दिया गया है:
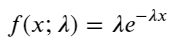
फिटिंग के माध्यम से, यह पाया गया कि परिणाम पॉइसन वितरण के अपेक्षित परिणामों से काफी भिन्न थे। पॉइसन प्रक्रिया ने लंबे अंतराल की आवृत्ति को कम करके आंका और छोटे अंतराल की आवृत्ति को अधिक करके आंका। (वास्तविक अंतराल वितरण संशोधित पैरेटो वितरण के करीब है)
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
trades = pd.read_csv('YGGUSDT-aggTrades-2023-08-05.csv')
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
buy_trades.index = buy_trades['date']
buy_trades['interval'][buy_trades['interval']<1000].plot.hist(bins=200,figsize=(10, 5));
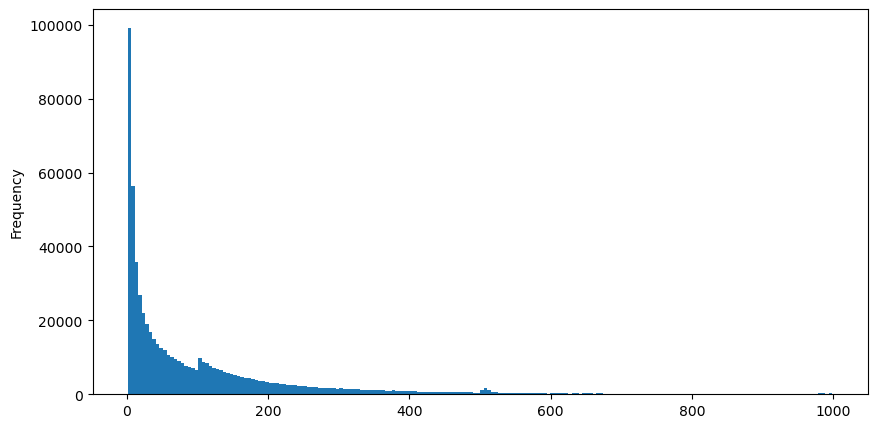
Intervals = np.array(range(0, 1000, 5))
mean_intervals = buy_trades['interval'].mean()
buy_rates = 1000/mean_intervals
probabilities = np.array([np.mean(buy_trades['interval'] > interval) for interval in Intervals])
probabilities_s = np.array([np.e**(-buy_rates*interval/1000) for interval in Intervals])
plt.figure(figsize=(10, 5))
plt.plot(Intervals, probabilities)
plt.plot(Intervals, probabilities_s)
plt.xlabel('Intervals')
plt.ylabel('Probability')
plt.grid(True)
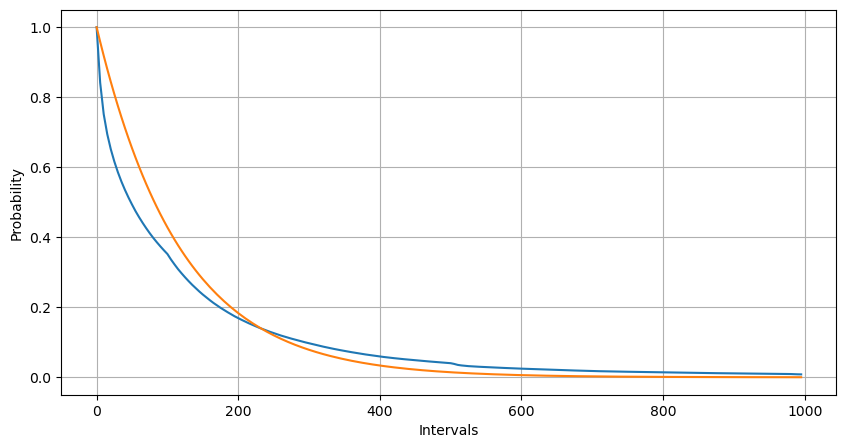
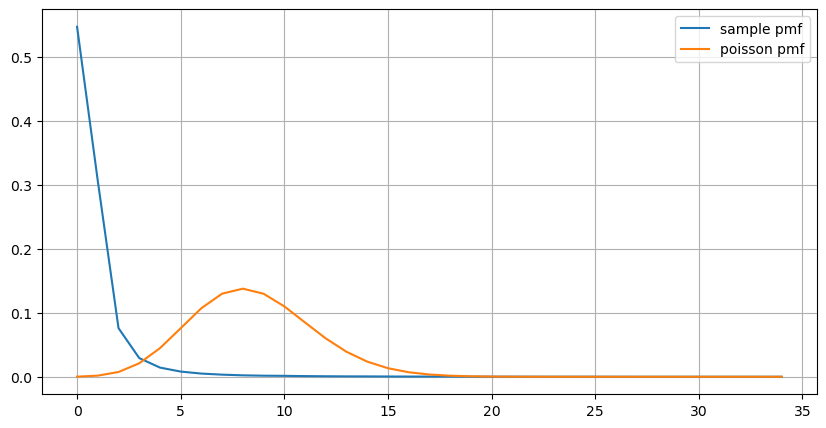
एक सेकण्ड के भीतर होने वाले ऑर्डरों की संख्या का सांख्यिकीय वितरण और पॉइसन वितरण के साथ तुलना भी बहुत स्पष्ट अंतर दिखाती है। पॉइसन वितरण कम-संभाव्यता वाली घटनाओं की आवृत्ति को महत्वपूर्ण रूप से कम करके आंकता है। संभावित कारण:
- घटना की गैर-स्थिर दर: पॉइसन प्रक्रिया यह मानती है कि किसी भी समयावधि में होने वाली घटनाओं की औसत दर स्थिर होती है। यदि यह धारणा सही नहीं है, तो डेटा का वितरण पॉइसन वितरण से विचलित हो जाएगा।
- प्रक्रियाओं की अंतःक्रिया: पॉइसन प्रक्रिया की एक अन्य बुनियादी धारणा यह है कि घटनाएँ एक दूसरे से स्वतंत्र होती हैं। यदि वास्तविक विश्व की घटनाएं एक-दूसरे को प्रभावित करती हैं, तो उनका वितरण पॉइसन वितरण से विचलित हो सकता है।
दूसरे शब्दों में, वास्तविक वातावरण में, ऑर्डर की आवृत्ति गैर-स्थिर होती है, इसे वास्तविक समय में अद्यतन करने की आवश्यकता होती है, और प्रोत्साहन उत्पन्न होंगे, अर्थात, एक निश्चित समय में अधिक ऑर्डर अधिक ऑर्डर को प्रोत्साहित करेंगे। इससे रणनीति में एक भी पैरामीटर तय करना असंभव हो जाता है।
result_df = buy_trades.resample('0.1S').agg({
'price': 'count',
'quantity': 'sum'
}).rename(columns={'price': 'order_count', 'quantity': 'quantity_sum'})
count_df = result_df['order_count'].value_counts().sort_index()[result_df['order_count'].value_counts()>20]
(count_df/count_df.sum()).plot(figsize=(10,5),grid=True,label='sample pmf');
from scipy.stats import poisson
prob_values = poisson.pmf(count_df.index, 1000/mean_intervals)
plt.plot(count_df.index, prob_values,label='poisson pmf');
plt.legend() ;
वास्तविक समय अद्यतन पैरामीटर
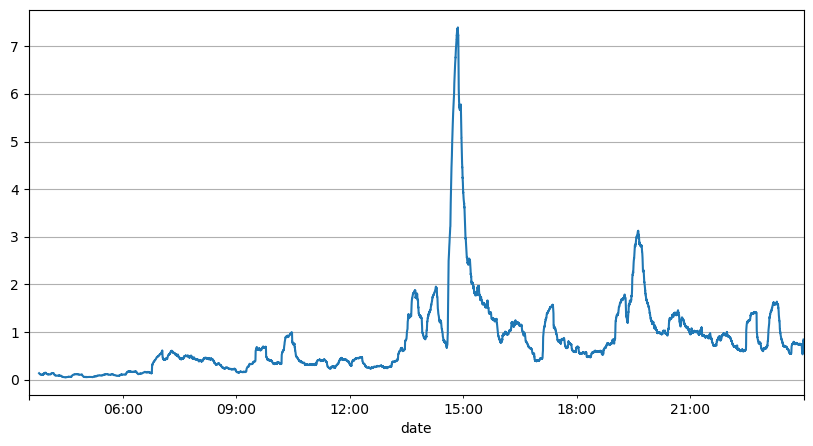
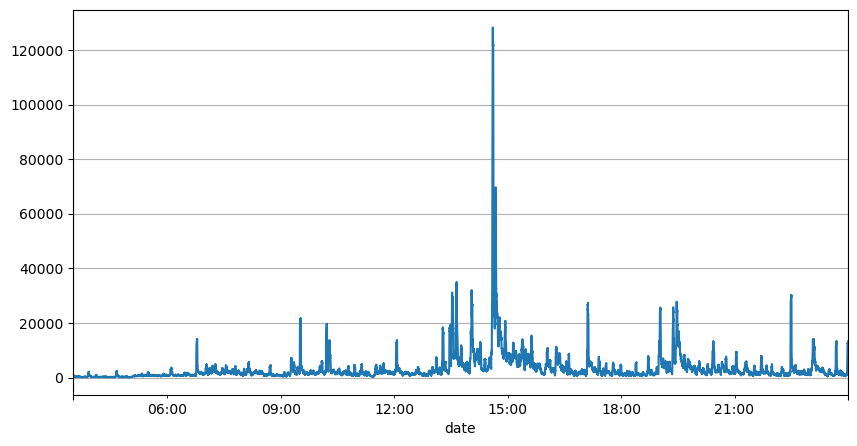
ऑर्डर अंतराल के पिछले विश्लेषण से पता चलता है कि निश्चित पैरामीटर वास्तविक बाजार स्थितियों के लिए उपयुक्त नहीं हैं, और रणनीति के बाजार विवरण के प्रमुख पैरामीटर को वास्तविक समय में अद्यतन करने की आवश्यकता है। सबसे आसान समाधान स्लाइडिंग विंडो का मूविंग एवरेज है। नीचे दिए गए दो आंकड़े 1 सेकंड के भीतर खरीद ऑर्डर की आवृत्ति और ट्रेडिंग वॉल्यूम की 1000 विंडो का औसत हैं। यह देखा जा सकता है कि लेन-देन में एक क्लस्टरिंग घटना है, यानी ऑर्डर की आवृत्ति सामान्य से काफी अधिक है। समय की अवधि, और इस समय वॉल्यूम भी समकालिक रूप से बढ़ जाता है। यहां, पिछले माध्य का उपयोग नवीनतम सेकण्ड के मान का पूर्वानुमान लगाने के लिए किया जाता है, तथा अवशिष्ट की माध्य निरपेक्ष त्रुटि का उपयोग पूर्वानुमान की गुणवत्ता को मापने के लिए किया जाता है।
ग्राफ से हम यह भी समझ सकते हैं कि ऑर्डर आवृत्ति पॉइसन वितरण से इतनी अधिक क्यों विचलित होती है। हालाँकि प्रति सेकंड ऑर्डर की औसत संख्या केवल 8.5 गुना है, लेकिन चरम मामलों में प्रति सेकंड ऑर्डर की औसत संख्या इससे बहुत अधिक विचलित होती है।
यहां पाया गया कि अवशिष्ट त्रुटि की भविष्यवाणी करने के लिए पिछले दो सेकंड के माध्य का उपयोग करना सबसे छोटा है और सरल माध्य भविष्यवाणी परिणाम से कहीं बेहतर है।
result_df['order_count'][::10].rolling(1000).mean().plot(figsize=(10,5),grid=True);
result_df
| order_count | quantity_sum | |
|---|---|---|
| 2023-08-05 03:30:06.100 | 1 | 76.0 |
| 2023-08-05 03:30:06.200 | 0 | 0.0 |
| 2023-08-05 03:30:06.300 | 0 | 0.0 |
| 2023-08-05 03:30:06.400 | 1 | 416.0 |
| 2023-08-05 03:30:06.500 | 0 | 0.0 |
| … | … | … |
| 2023-08-05 23:59:59.500 | 3 | 9238.0 |
| 2023-08-05 23:59:59.600 | 0 | 0.0 |
| 2023-08-05 23:59:59.700 | 1 | 3981.0 |
| 2023-08-05 23:59:59.800 | 0 | 0.0 |
| 2023-08-05 23:59:59.900 | 2 | 534.0 |
result_df['quantity_sum'].rolling(1000).mean().plot(figsize=(10,5),grid=True);
(result_df['order_count'] - result_df['mean_count'].mean()).abs().mean()
6.985628185332997
result_df['mean_count'] = result_df['order_count'].ewm(alpha=0.11, adjust=False).mean()
(result_df['order_count'] - result_df['mean_count'].shift()).abs().mean()
0.6727616961866929
result_df['mean_quantity'] = result_df['quantity_sum'].ewm(alpha=0.1, adjust=False).mean()
(result_df['quantity_sum'] - result_df['mean_quantity'].shift()).abs().mean()
4180.171479076811
संक्षेप
यह आलेख संक्षेप में उन कारणों का परिचय देता है कि क्यों ऑर्डर समय अंतराल पॉइसन प्रक्रिया से विचलित हो जाता है, मुख्यतः इसलिए क्योंकि पैरामीटर समय के साथ बदलते हैं। बाजार का अधिक सटीक पूर्वानुमान लगाने के लिए, रणनीति को बाजार के बुनियादी मापदंडों पर वास्तविक समय की भविष्यवाणियां करने की आवश्यकता होती है। अवशेषों का उपयोग पूर्वानुमानों की गुणवत्ता को मापने के लिए किया जा सकता है। उपरोक्त उदाहरण सबसे सरल है। समय श्रृंखला विश्लेषण, अस्थिरता एकत्रीकरण आदि पर कई संबंधित अध्ययन हैं, जिन्हें और बेहतर बनाया जा सकता है।