Mengejar Gadis dan Menemukan Rudal - Statistik Formula Bayesian

• ### ONE

Orang-orang yang tidak mengerti gaya hidup yang rasional pasti akan mengalami kejadian sedih dalam kehidupan emosional: kebetulan bertemu dengan seorang gadis cantik yang sesuai dengan hati, sejak itu berpikir, tidur dan makan, memulai perjalanan cinta yang panjang, menunggu sampai suatu hari, dalam perselisihan yang tak ada habisnya, akhirnya mengumpulkan keberanian untuk mengaku kepada gadis itu, hasilnya gadis itu mengatakan bahwa saya sudah memiliki pacar yang bahagia seperti burung hantu, sangat sulit untuk diterima …

Untuk menghindari ketidaknyamanan ini, bagaimana cara menentukan apakah seorang gadis lajang atau tidak menjadi pelajaran wajib.

Jika Anda bekerja dengan seorang gadis dan sering berada di dekatnya, tidak sulit untuk mengetahui apakah dia lajang atau tidak. Namun, tugas yang sulit yang harus diselesaikan oleh orang-orang yang rasional adalah: sebagai orang asing yang menjaga jarak dengan gadis itu, tanpa disadari oleh gadis itu, Anda dapat menilai status lajang gadis itu dengan informasi terbatas yang ada di tangan Anda.

Langkah pertama, percayalah pada naluri Anda. Orang yang rasional dapat mempertimbangkan untuk mencari beberapa teman bersama untuk diam-diam mengamati gadis target, tentu saja orang yang dicari tidak harus menjadi orang yang rasional, apa yang diidentifikasi oleh kelompok hati, penghancur rumor, pengendali alam, dokter forensik kriminal sebaiknya mencari beberapa orang, orang yang sudah menikah, orang tua, pencuri bunga juga harus mencari, semakin banyak orang, semakin baik, semakin beragam.

Untuk itu, kita harus melakukan langkah kedua, berbicara dengan fakta dan bukti. Apakah seorang wanita lajang atau tidak, jawabannya bisa dicari dari banyak detail.

Seperti melakukan penelitian ilmiah, Anda dapat mencari informasi terlebih dahulu, dengan mencari di google Anda dapat menemukan kriteria single yang mudah digunakan yang telah dipelajari oleh banyak orang kesepian selama bertahun-tahun, seperti prinsip ponsel (anak perempuan yang jatuh cinta lebih sering menggunakan ponsel), prinsip belajar sendiri (anak perempuan yang lajang sering belajar sendiri dengan beberapa teman perempuan). Setelah itu, lakukan tes statistik di sekitar Anda untuk mengetahui apakah anak perempuan yang lajang atau tidak, tentu saja, semakin besar sampelnya, semakin baik hasilnya.

Ini adalah nilai statistik seperti itu.

Ketika semua data dari percobaan kecantikan ini tersedia, kita dapat melanjutkan dan mengomentari dan mengoptimalkan nilai probabilitas 65,65% yang baru saja dipilih. Bergantung pada apa? Tentu saja, ini adalah kinerja gadis target dalam berbagai kriteria.

Jadi sekarang target mm adalah probabilitas untuk menjadi jomblo berubah menjadi

Saya tidak tahu apa yang akan terjadi dengan saya, tapi saya pikir saya akan menjadi lebih baik jika saya tidak melakukan ini.

Jika hasil penelitian ini juga menemukan bahwa di antara gadis-gadis lajang, penggunaan ponsel lebih dari 1,2 kali/jam menyumbang 20% dari jumlah tersebut; di antara gadis-gadis yang sudah jatuh cinta, angka tersebut adalah 60%. Untuk gadis target, hasil observasi menunjukkan bahwa penggunaannya lebih dari 1,2 kali/jam, maka hasil probabilitasnya diperbarui.

Kemungkinan untuk menjadi jomblo kembali turun secara tragis menjadi 56.02%, orang-orang yang berpikir logis bisa mencari lebih banyak kriteria penilaian, melakukan lebih banyak penelitian, terus-menerus memperbarui nilai probabilitas jomblo gadis, membuatnya semakin dekat dengan fakta, tetapi sebelum mendapatkan hasil akhir, Anda harus menetapkan nilai ambang: probabilitas jomblo gadis melebihi nilai ambang ini (misalnya 90%), Anda layak untuk mengaku, jika tidak, langsung matilah.

Namun perlu dicatat bahwa tidak peduli berapa kali perhitungan, hasilnya akhirnya adalah nilai probabilitas, bukan fakta, bahkan setelah beberapa penelitian, sudah dapat menentukan probabilitas tunggal gadis target menjadi 99.9%, segera siap untuk mengakuinya, tetapi dalam penelitian terakhir tentang observasi gadis, menemukan orang dan seorang pria berjabat tangan dan tertawa, berpelukan bersama, maka, probabilitas tunggal gadis akan langsung turun dari 99.9% menjadi mendekati 0, konsekuensinya dapat diprediksi …

Metode Bayesian sederhana adalah bahwa probabilitas awal + bukti baru = probabilitas setelah koreksi, tidak dibatasi oleh jumlah informasi, dapat menggabungkan hasil dari berbagai sumber, termasuk penilaian subyektif dan informasi objektif yang terbatas, untuk mendapatkan kesimpulan akhir. Di sini dinyatakan dengan tegas bahwa metode ini memiliki risiko tertentu, perlu berhati-hati ketika mencoba, dan anak-anak kecil tidak harus mencobanya.

Namun, tidak boleh dipandang remeh oleh Bayesian Metaphysics, yang telah digunakan oleh Angkatan Laut AS untuk mencari bom hidrogen yang hilang di Samudera Pasifik dan kapal selam nuklir yang hilang, dan di bawah ini kita beralih dari saluran emosional ke saluran sejarah.

• ### TWO

Pada suatu hari pada bulan Januari 1966, sebuah pesawat B-52 Amerika Serikat terbang di atas Palomarés, Spanyol, dengan beberapa pilot di pesawat melakukan tugas pengisian bahan bakar udara yang disiapkan oleh Komando Angkatan Udara. Secara logis, penerbangan ini tidak berbahaya, dan pilotnya adalah orang yang sangat tenang, tidak suka membawa pipa besar, bahkan di kabin pesawat. Namun, kapten dan beberapa orang di dalam pertemuan ini mengalami masalah besar, dan tidak dapat lagi menikmati pipa besar.

Namun, kisahnya belum berakhir, setelah itu terjadi serangkaian tragedi dan komedi.

Untuk menemukan bom yang hilang, Amerika Serikat dengan cepat mengerahkan pasukan pencarian dari dalam negeri yang terdiri dari beberapa ahli ke lokasi, termasuk seorang matematikawan bernama John Craven, yang bergelar Chief Scientist of the US Navy Special Programs.

Dalam masalah mencari bom hidrogen, proposal Craven menggunakan metode Bayesian yang baru saja disebutkan, ia mengumpulkan para ahli dari berbagai bidang, tetapi masing-masing memiliki bidang keahliannya sendiri, dan tidak universal. Beberapa orang tahu banyak tentang bom B-52, tetapi sedikit yang diketahui tentang karakteristik bom hidrogen.

Untuk berbagai pertanyaan ini, Craven meminta para ahli untuk membuat berbagai asumsi, membayangkan berbagai skenario, dan kemudian menebak probabilitas bom hidrogen di berbagai lokasi dalam berbagai situasi, dan kemungkinan munculnya setiap situasi.

Cara Craven juga ditantang oleh rekan-rekannya, karena dalam programnya, banyak hasil yang diperoleh para ahli ini dalam bentuk tebakan, pemungutan suara atau bahkan bisa dikatakan perjudian, tidak dapat menjamin keakuratan semua hasil, tetapi karena tugas mencari bom berton-ton, tidak ada waktu untuk melakukan eksperimen yang tepat dan membangun teori yang lengkap dan dapat diandalkan, cara Craven tidak diragukan lagi merupakan cara yang layak.

Craven mendapatkan hasil dari para ahli yang mengundang untuk bersetubuh, dan setelah digabungkan, ia menggambar sebuah peta probabilitas lokasi bom hidrogen: ia membagi seluruh area yang mungkin menjadi banyak kotak kecil, masing-masing dengan nilai probabilitas yang berbeda, dengan tinggi dan rendah, seperti garis yang sama tinggi yang menunjukkan puncak dan lembah di peta. Seperti para penganut rasionalitas yang memutuskan apakah seorang gadis lajang atau tidak, Craven menyelesaikan langkah pertama dari metode Bayesian.

Setelah itu, Craven bersama dengan komandan pasukan pencarian mulai mencari peledak, memperbarui probabilitas setiap grid pada saat yang sama dalam proses pencarian, namun, lokasi yang ditunjukkan oleh kotak dengan probabilitas terbesar sering kali adalah jurang yang sulit di darat dan daerah laut dalam, dan bahkan jika peledak benar-benar ada, tidak selalu dapat ditemukan, sehingga perlu untuk membuat peta probabilitas lain yang menunjukkan peledak sudah ada, dan kemungkinan yang dapat ditemukan adalah peledak daripada kemungkinan lokasi peledak.

Hanya dua tahun kemudian, pada tahun 1968, Craven mendapat kesempatan untuk bermain lagi, dan kehilangan satu lagi peluru kecil, yang kali ini Navy AS kehilangan satu lagi yang besar.

Pada bulan Juni 1968, kapal selam nuklir Angkatan Laut, Swan, menghilang di Samudera Pasifik, dan 99 orang di kapal selam dan kapal hilang tanpa suara. Menurut laporan investigasi setelah kejadian, penyebabnya adalah sebuah torpedo aneh di kapal selam, yang ditembakkan ke luar dan kemudian menembak dirinya sendiri, menyebabkan peluru meledak di kapal selam.

Untuk mencari lokasi Swan, Angkatan Laut Amerika Serikat melakukan pencarian besar-besaran, dan Craven tentu saja ikut serta. Karena kecepatan kapal selam berlayar dengan cepat pada saat kecelakaan, arah, besarnya arah dampak ledakan, dan arah tiupan kapal selam pada saat ledakan tidak diketahui, bahkan jika diketahui di mana kapal selam meledak, sulit untuk menentukan di mana puing-puing kapal selam akhirnya terendam air laut.

Tidak ada ahli yang dapat memperkirakan dengan tepat apa yang terjadi pada kapal selam sebelum dan sesudah peristiwa itu, dan seperti pada saat mencari peledak, Craven berkonsultasi dengan ahli matematika, ahli kapal selam, dan ahli dalam berbagai bidang penyelamatan maritim, menulis berbagai skenario yang mungkin, dan membiarkan mereka menebak ke arah mana situasi itu akan berkembang sesuai dengan pengetahuan dan pengalaman mereka.

Pada akhirnya, Craven mendapatkan sebuah peta probabilitas dari 20 mil laut. Seluruh laut dibagi menjadi banyak grid kecil, masing-masing dengan dua nilai probabilitas p dan q, di mana p adalah probabilitas bahwa kapal selam berada di grid ini, dan q adalah probabilitas bahwa kapal selam akan ditemukan jika berada di grid ini.

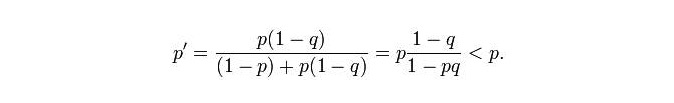
Jika Anda tidak tahu apa yang terjadi, maka kemungkinan keberadaan kapal selam di setiap grid lainnya akan meningkat:

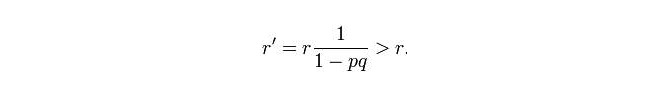
Setiap pencarian dilakukan dengan memilih satu grid yang memiliki probabilitas tertinggi untuk ditemukan oleh kapal selam di seluruh wilayah. Jika tidak ditemukan, maka peta probabilitas akan dihapus dan kapal pencarian akan menuju ke grid yang paling mencurigakan untuk pencarian, dan terus menerus sampai ditemukan.

Pada awalnya, Angkatan Laut secara empiris memperkirakan bahwa kapal selam itu berada di dasar laut di sebelah timur titik ledakan, mengabaikan saran Craven dan matematikawan lainnya, tetapi setelah berbulan-bulan pencarian tidak berhasil. Kemudian Angkatan Laut harus mendengarkan saran Craven, yang menurut grafik probabilitas, kapal selam yang mengalami kecelakaan harus berada di sebelah barat titik ledakan. Setelah beberapa pencarian, kapal selam itu ditemukan di dasar laut di sebelah barat daya titik ledakan.

Setelah dua kali menunjukkan kekuatan, metode Bayes yang digunakan oleh Craven dalam pencarian maritim secara bertahap diterima secara luas, dan sejak itu, metode Bayes secara tidak terduga sering muncul di mana-mana sebagai kata kunci bersama dengan bom hidrogen, kapal selam nuklir. Selama beberapa dekade, aplikasi metode Bayes menjadi lebih luas, mulai dari filter kata pencarian google hingga mobil tanpa pengemudi untuk menentukan lokasi mereka sendiri.

Dikutip dari Modeling Matematika