Gauss dan Angsa Hitam

---

• ### Anggrek hitam

Saya memiliki julukan ahli teori keong, yang mungkin juga julukan untuk orang bodoh, karena saya memang sangat bodoh, lebih suka menyimpulkan prinsip dari banyak hal. Saya mahir dalam statistik, suka mencari rata-rata berbagai hal di sekitar saya, menangkap keong esensial mereka, dan mengabaikan berbagai detail yang kecil, berpikir bahwa hanya dengan memahami tren keseluruhan hal-hal, saya dapat mengubah prinsip keong di kepala saya menjadi kenyataan dalam hidup, tetapi kenyataannya adalah bahwa saya adalah orang bodoh yang membosankan dan bahkan membuat kelinci masak terbang.

Ayah saya tidak banyak membaca buku, tapi dia adalah seorang yang dikenal sebagai orang yang pandai, yang sering menang secara mengejutkan dalam kehidupan nyata.

Hal ini membuat saya, seorang teoritis, bingung, karena saya menganggap detail itu tidak penting, seperti suara di radio. Saya percaya pada Gaussian Distribution yang terkenal (lihat di bawah), yang mengatakan bahwa keberhasilan dan kegagalan tidak ditentukan oleh detail individu, tetapi oleh sifat-sifat keseluruhan. Sama seperti saya mungkin kehilangan pacar saya karena satu kencan tanpa membawa dompet, tetapi saya memiliki banyak kencan dengan banyak wanita dalam hidup saya, dan jika saya baik-baik saja, saya akan memiliki keseluruhan.

Namun, apa yang dikatakan ayah ternyata tidak benar.

Jadi saya berpikir, apa yang salah dengan dunia yang selalu saya banggakan yang terdiri dari kurva Gaussian yang indah ditambah dengan hukum Newton yang harmonis? Saya mulai mempelajari biologi dan menemukan jawabannya di dunia hewan pengerat, karena ada satu hewan, yaitu burung hantu hitam.

Sebelum burung hantu hitam muncul, burung hantu di danau burung hantu adalah putih salju, dan Anda dapat membayangkan bagaimana rasanya jika jutaan burung hantu putih terbang di atas danau biru langit itu, terlihat seperti salju di Mazaros. Jadi saya pikir itu adalah simbol burung hantu putih, dan saya memprediksi burung hantu putih dengan probabilitas 100%. Sampai suatu hari burung hantu hitam murni terbang di atas danau, seolah-olah berasal dari luar angkasa, dan menghancurkan impian saya tentang burung hantu siang hari. Dari sini saya mengerti bahwa di dunia makhluk hidup, yang unik adalah esensi, bukan rata-rata.

Dunia fisika klasik adalah dunia rata-rata, detail dan ekstensi dapat dibuang. Tetapi begitu masuk ke bidang yang didominasi oleh makhluk hidup, mereka menjadi raja.

Sebelum memasuki dunia biologis yang kotor dan berantakan, marilah kita mengenang tarian tarian siang hari yang dipimpin oleh hukum Gauss.

• ### Pembagian Gauss dan Teorema Bilangan Besar Kekuatan rata-rata

Kita sering menggunakan rata-rata untuk menyatakan keadaan umum dari sesuatu, seperti tinggi pria Cina adalah 1 meter 7, dan untuk orang-orang yang melakukan statistik, rata-rata hampir menjadi kepercayaan, dan kita sering lupa asumsi dasar di balik kepercayaan ini - distribusi Gaussian, hanya jika hal-hal yang kita statistikkan memiliki distribusi Gaussian, rata-rata dapat benar-benar mewakili sifat-sifat sesuatu.

Keterangan: penjumlahan sama dengan rata-rata. Pengukuran rata-rata bergantung pada jumlah yang dibagi dengan data setelah penjumlahan banyak data. Ukuran deviasi sampel di sekitar rata-rata dinyatakan dengan perbedaan standar. Teori klasik memberi tahu kita bahwa semakin besar kapasitas sampel, semakin besar rata-rata yang mewakili kelompok yang diteliti.

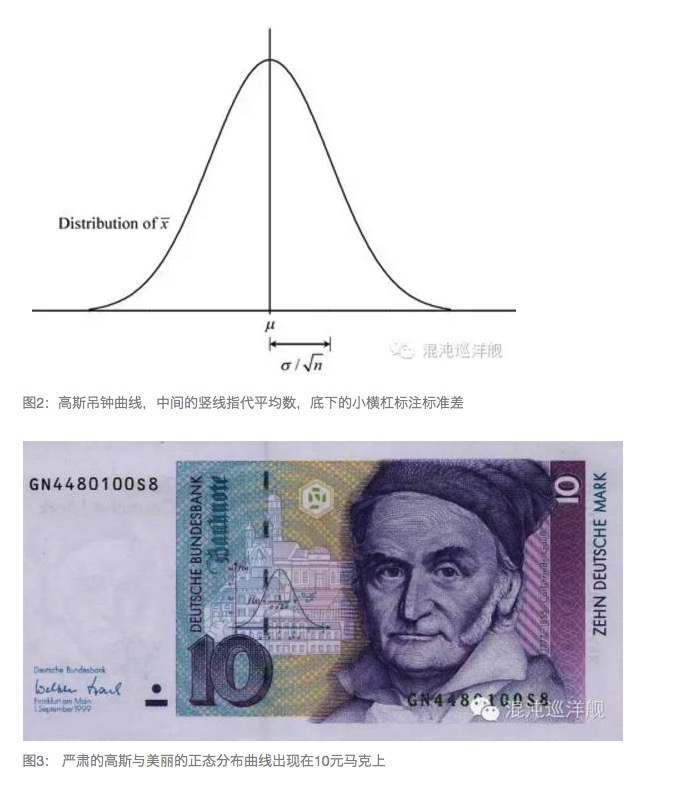
Gauss memberi tahu kita tentang kekuatan penjumlahan. Untuk sebuah peristiwa acak, seperti dadu di kasino, setiap hasil yang diperoleh dari satu sampai enam sama sekali tidak dapat diprediksi, tetapi jika Anda bertaruh 10.000 kali, dan menambahkan poin yang Anda dapatkan setiap kali Anda mendapatkan angka yang dapat diprediksi dengan semakin akurat. Hasil ini dapat digambarkan oleh sesuatu yang disebut kurva Gauss, yang memiliki dua karakteristik, rata-rata dan standar deviasi.

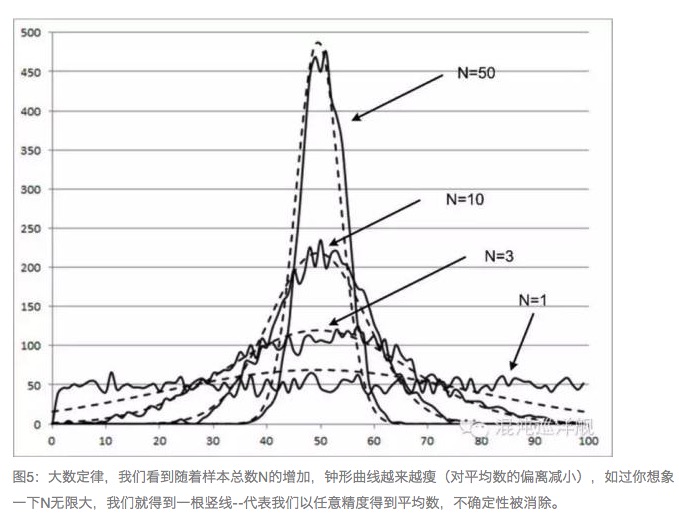
Kekuatan hukum hitung besar adalah bahwa ia memungkinkan sebuah dunia yang pasti dapat terjadi di atas ketidakpastian yang sangat besar. Sama seperti matahari akan terbit esok hari bunga musim semi akan melakukan hal ini, kita tahu bahwa probabilitas tidak terjadi adalah hampir 0. Sebenarnya adalah distribusi Gaussian dan jaminan dari teori hitung besar, karena matahari terbit bunga adalah hasil dari tindakan bersama dari matahari dan bunga yang terdiri dari banyak atom dan molekul, ketika berkeringat pada serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian serangkaian ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser ser

Distribusi normal dan Teorema Bilangan Besar adalah akar dari semua kepastian, karena dunia yang kita lihat adalah hasil dari penjumlahan terus-menerus dari banyak faktor mikro yang tidak pasti.

Wahyu tentang pentingnya detail: Dia memberi tahu kita bahwa ketika ada cukup banyak faktor yang menentukan suatu peristiwa, dan jumlah percobaan yang cukup besar, setiap detail kecil tidak lagi penting, karena mereka disetarakan dalam jumlah besar.

Tapi jangan terlalu cepat.

• ### Perangkap di Balik Hukum Gauss

A. Faktor-faktor detail yang independen

Sepertinya agak abstrak, tetapi sebenarnya adalah bahwa faktor-faktor penambahan-yang-membuat-sesuatu-tidak-bisa-berkomunikasi secara pribadi, seolah-olah jika semua wanita yang Anda kenal bersekongkol secara pribadi untuk mengatakan bahwa Anda baik atau buruk, maka tidak banyak lagi orang yang Anda kencan akan mendapatkan hasil yang ditentukan oleh rata-rata yang ideal. Karena semua wanita sebenarnya mendapatkan ide yang sama dengan orang yang Anda kencan.

B. Perpindahan waktu

Ini sedikit aneh. Sebagai contoh sederhana, jika Anda melemparkan bola yang digantikan, menjadi bola yang ditambah organ, setiap sisi adalah satu titik, dan kemudian sering diganti dari waktu ke waktu, maka Anda tidak akan pernah mendapatkan rata-rata yang stabil, seperti Anda masih di sana dengan Gaussian penjumlahan, berharap Anda akan akhirnya memenangkan jumlah uang yang diberikan oleh rata-rata, adalah orang bodoh yang ditipu.

Teorema pluralitas adalah dasar dari pengetahuan kita tentang dunia acak, ia memberi tahu kita bagaimana kepastian muncul dari dasar kebetulan. Tetapi ia seperti hukum pertama Newton dan model gas ideal, permukaan yang halus dan partikel dasar yang tidak berinteraksi sama sekali tidak ada di dunia makhluk hidup nyata, meskipun kita memang mendapatkan beberapa situasi yang mendekati pada beberapa waktu.

• ### Efek Swan Hitam dan Distribusi Timbul

Kurva Gaussian dan hukum-hukum besar mengatur dunia fisika teoritis yang mulia, di mana belajar dengan baik dapat meningkat dari hari ke hari, Cinderella pasti akan bertemu dengan pangeran. Namun, Black Swan menghancurkan dongeng.

Sifat dari burung hantu hitam adalah individu terhadap keseluruhan, dan detail terhadap keseluruhan memiliki pengaruh yang menentukan. Ketika seekor burung hantu hitam muncul di permukaan air, sifat dari seluruh kelompok burung hantu berubah, dan seekor burung hantu dunia yang murni putih menjadi abu-abu.

Dari sudut pandang Gaussian normal, probabilitas munculnya black swan bisa diabaikan, karena kita telah memperhitungkan sampel daylight swan yang sangat besar sebelumnya, tetapi black swan tetap muncul, dan munculnya tampaknya tidak disengaja dan kebetulan, apakah kita sangat tidak beruntung?

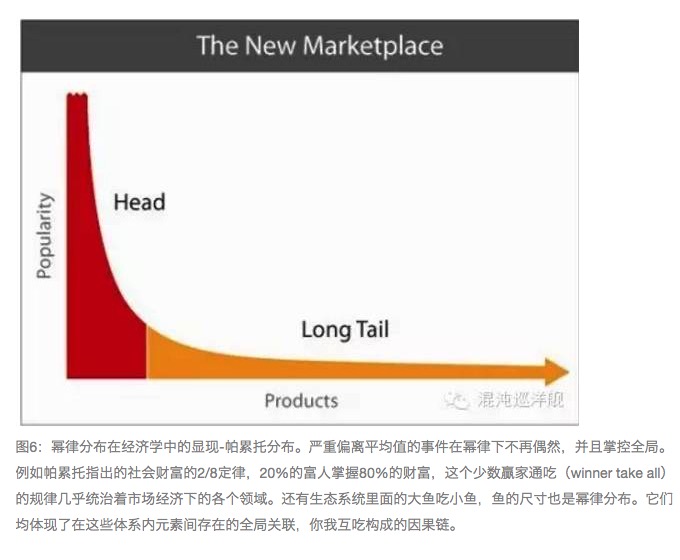
Di dunia makhluk hidup, yang dominan adalah distribusi power law, yang sebenarnya juga terkait dengan hak dan kekayaan (lihat Gambar 6, distribusi Pareto). Ekspresi matematis dari distribusi power law sangat sederhana, dan distribusi yang berbeda hanya terwujud dalam perbedaan indeks pixel.

Mengapa pengaruh black swan begitu besar? - Di sini teori fase dalam fisika modern memberikan jawaban yang sangat kuat. Saya memberi contoh khusus - gunung es. Gunung es adalah runtuhnya permukaan es di puncak gunung, yang seharusnya mengarah ke sebuah gunung es yang hampir tidak mungkin terjadi. Gunung es memenuhi definisi peristiwa black swan klasik, yang secara logika hampir tidak terjadi, dan jika terjadi, itu mematikan.

Keadaan kritis adalah keadaan keseimbangan yang rapuh, kekuatan yang mempertahankan es yang bersatu hampir sama dengan kekuatan yang memusnahkan es, tetapi tidak dapat diperbaiki. Jika Anda melemparkan sepotong batu kecil di lereng salju yang besar, efek batu itu tidak diserap oleh es lokal tetapi menyebar ke seluruh es, seperti jerami terakhir yang menekan unta mati, yang membuat keseimbangan keseluruhan terbalik.

“Kritik membuat Black Swan menjadi kekuatan yang menentukan”.

Inti dari teori avalanche adalah pembesaran tak terbatas dari peran detail pada keadaan kritis. Faktor kecil yang seharusnya terbatas pada keadaan lokal menyebar ke seluruh tubuh pada keadaan kritis. Teori avalanche tersebar di berbagai bidang, seperti gempa bumi, runtuhnya pasar saham, krisis keuangan, dan bahkan ledakan revolusi sosial.

Dalam sebuah pertempuran yang merata, setiap peran kecil individu dapat diperbesar dan memengaruhi medan perang. Misalnya, dalam sebuah pertandingan yang merata di kedua sisi kekuatan yang sama, seorang anggota tim berbunyi ponselnya, dan dia menjadi panik, dan efeknya menyebabkan panik menyebar ke seluruh tim, dan akhirnya pertandingan hancur karena lonceng ponsel.

Karena itu, segala sesuatu yang berkaitan dengan makhluk hidup, termasuk sejarah makhluk hidup dan sejarah kita sebagai manusia dan kehidupan kita masing-masing, terjadi pada keadaan kritis, keadaan yang penuh dengan salju besar dan kecil, detail yang tidak dapat diprediksi yang menentukan keadaan keseluruhan. Karena Anda masih hidup besok, burung hantu hitam akan terbang.

Catatan: Evolusi biologis adalah efek black swan yang paling primitif, varian dari makhluk yang sudah menjadi keanehan, dan varian yang bisa bertahan hidup adalah keanehan yang lebih dari keanehan, dan itu adalah keanehan yang tidak mainstream (rata-rata) yang mendominasi evolusi makhluk.

Black Swan membawa ketidakpastian yang mendalam ke dalam kehidupan kita sehari-hari, dan bagi saya sebagai seorang teoritis, dunia yang penuh dengan garis lurus yang sempurna, garis paralel, dan hukum-hukum Newton terasa seperti sebuah kota kosong. Dengan beton besi yang besar, ia masih mendukung industri modern, dan bahkan membawa kita untuk menemukan rahasia Black Swan, tetapi tidak memungkinkan kita untuk memahami diri kita sendiri.

• Wahyu

  • #### Black Swan Positif - Menghadapi Kesempatan:

Hidup itu keras. Budaya kita mendorong pahlawan, dan sejarah ditulis oleh orang-orang yang selamat. Hiduplah dengan baik, hati terbuka, mata terbuka, dan bersiaplah, Anda akan memiliki lebih banyak kesempatan untuk menunggu pelangi hitam Anda.

• #### Black Swan Negatif - Tairan Berhadapan Dengan Risiko:

Karakteristik burung hantu hitam adalah hitam, ia bersembunyi di kegelapan sebelum muncul, bahkan jika ia melihat Anda dari belakang, Anda masih tidak bisa tahu. Berpikir di sini saya tidak khawatir. Karena yang disebut risiko yang diketahui tidak berbahaya, Anda tidak bisa tahu risiko sebenarnya.

• #### Pengendalian risiko:

Hentikan kerusakan. Ketika badai salju hitam datang, satu-satunya hal yang dapat dilakukan adalah membatasi dampaknya secara lokal tanpa menyebabkan terjadinya hujan es.

• #### Perlakuan terhadap akademisi:

Jangan meremehkan Gauss, karena bahkan distribusi logis, hanya dengan memahami Gauss, kita bisa memahami nilainya.

Dibawah ini foto-fotonya.