Tujuh teknik regresi yang harus Anda kuasai

**Artikel ini menjelaskan analisis regresi dan keunggulan-keunggulannya, dengan fokus menyimpulkan tujuh teknik regresi yang paling umum digunakan dan elemen-elemen kunci yang harus dikuasai, seperti regresi linier, regresi logis, regresi polinomial, regresi bertahap, regresi gelung, regresi seret, regresi ElasticNet, dan akhirnya menginformasikan faktor-faktor kunci untuk memilih model regresi yang benar. ** ** Analisis regresi tombol editor adalah alat penting untuk memodelkan dan menganalisis data. Artikel ini menjelaskan apa yang dimaksud dengan analisis regresi dan keunggulan-keunggulannya, dengan fokus pada pengelompokan tujuh teknik regresi yang paling umum digunakan dan elemen-elemen kunci untuk memilih model regresi yang benar, seperti regresi linier, regresi logis, regresi multipolar, regresi bertahap, regresi gelung, regresi loop, dan regresi ElasticNet.**

• ### Apa itu Regression Analysis?

Analisis regresi adalah teknik pemodelan prediktif yang mempelajari hubungan antara variabel akibat (target) dan variabel akibat (predikator). Teknik ini biasanya digunakan untuk analisis prediktif, model urutan waktu, dan hubungan sebab akibat antara variabel yang ditemukan. Sebagai contoh, hubungan antara pengemudi yang membabi buta dan jumlah kecelakaan lalu lintas jalanan, metode terbaik untuk penelitian adalah regresi.

Analisis Regresi adalah alat penting untuk memodelkan dan menganalisis data. Di sini, kita menggunakan kurva/garis untuk mencocokkan titik-titik data, dengan cara ini, perbedaan jarak dari kurva atau garis ke titik data adalah minimal.

• ### Mengapa kita menggunakan analisis regresi?

Seperti yang telah disebutkan di atas, analisis regresi memperkirakan hubungan antara dua atau lebih variabel. Di bawah ini, mari kita berikan contoh sederhana untuk memahaminya:

Misalnya, dalam kondisi ekonomi saat ini, Anda ingin memperkirakan pertumbuhan penjualan sebuah perusahaan. Sekarang, Anda memiliki data terbaru dari perusahaan yang menunjukkan bahwa pertumbuhan penjualan sekitar 2,5 kali pertumbuhan ekonomi. Dengan menggunakan analisis regresi, kita dapat memprediksi penjualan perusahaan di masa depan berdasarkan informasi saat ini dan masa lalu.

Ada banyak manfaat dari analisis regresi, seperti:

Ini menunjukkan hubungan yang signifikan antara variabel-faktor dan variabel-faktor;

Ini menunjukkan intensitas pengaruh dari beberapa variabel as pada satu variabel as.

Analisis regresi juga memungkinkan kita untuk membandingkan interaksi antara variabel yang mengukur skala yang berbeda, seperti hubungan antara perubahan harga dan jumlah kegiatan promosi. Ini berguna untuk membantu peneliti pasar, analis data, dan ilmuwan data untuk mengecualikan dan memperkirakan sekelompok variabel terbaik untuk membangun model prediksi.

• ### Berapa banyak teknologi regresi yang kita miliki?

Ada berbagai macam teknik regresi yang digunakan untuk membuat prediksi. Teknik-teknik ini terdiri dari tiga ukuran utama: jumlah variabel yang dikendalikan, jenis variabel yang dikendalikan, dan bentuk garis regresi. Kami akan membahasnya secara rinci di bagian berikut.

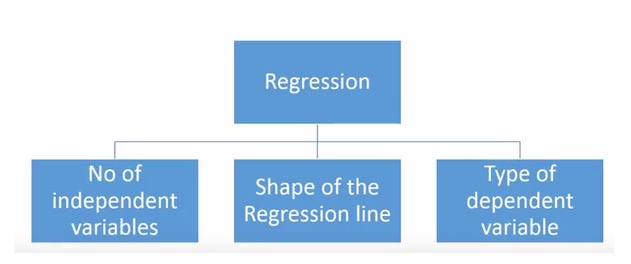
Untuk orang-orang yang kreatif, Anda bahkan dapat membuat model regresi yang belum pernah digunakan jika Anda merasa perlu menggunakan kombinasi parameter di atas. Tetapi sebelum Anda mulai, ketahuilah metode regresi yang paling umum digunakan:

• 1. Regressi Linear

  Ini adalah salah satu teknik pemodelan yang paling dikenal. Regressi linier biasanya merupakan salah satu teknik yang dipilih untuk mempelajari model prediksi. Dalam teknik ini, karena variabelnya berurutan, variabelnya sendiri dapat berurutan atau terpisah, sifat garis regresi adalah linier.

  Regresi linier menggunakan garis lurus asimetris terbaik (yang disebut garis regresi) untuk membangun hubungan antara variabel induk (Y) dan satu atau lebih variabel induk (X).

  Kita bisa menuliskannya dalam sebuah persamaan, yaitu y = a + b.*X + e, di mana a adalah jarak, b adalah kemiringan garis lurus, dan e adalah nilai kesalahan. Persamaan ini dapat digunakan untuk memprediksi nilai variabel target berdasarkan variabel prediksi yang diberikan (s).

  

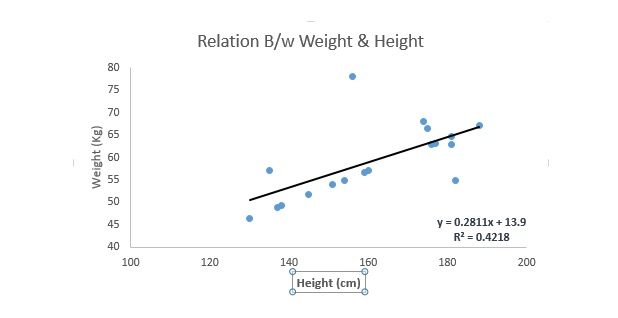
  Regressi unilinear berbeda dengan regressi multilinear karena regressi multilinear memiliki 1 variabel, sedangkan regressi unilinear biasanya hanya memiliki 1 variabel. Pertanyaannya adalah bagaimana kita mendapatkan garis yang paling sesuai?

  Bagaimana cara mendapatkan nilai dari garis kecocokan terbaik (a dan b)?

  Masalah ini dapat dengan mudah diselesaikan dengan menggunakan penggandaan minimal dua. Penggandaan minimal dua juga merupakan metode yang paling umum digunakan untuk menyamakan garis regresi. Untuk data observasi, ia menghitung garis kesesuaian optimal dengan meminimalkan jumlah kuadrat penyimpangan vertikal dari setiap titik data ke garis. Karena penyimpangan pertama kuadrat ketika dijumlahkan, maka nilai positif dan negatif tidak diimbangi.

  

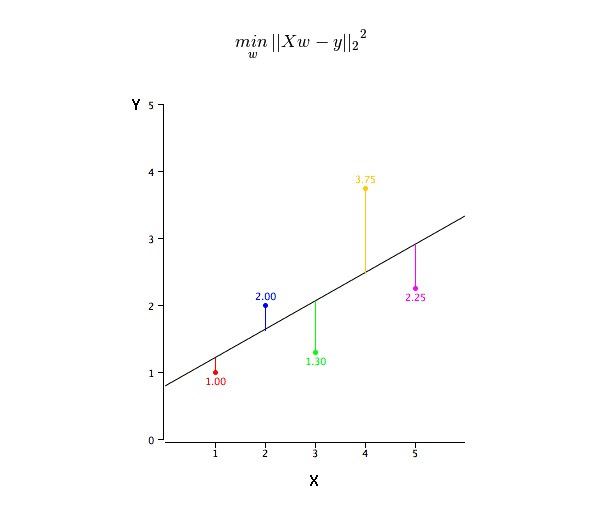
  Kita dapat menggunakan indikator R-square untuk menilai kinerja model. Untuk informasi lebih lanjut tentang indikator-indikator ini, dapat dibaca: Model Performance Indicators Part 1, Part 2.

  Intinya:

  • Harus ada hubungan linear antara variabel-faktor dan variabel-faktor
  • Regressi pluralitas memiliki banyak ko-linearitas, korelasi dan diferensiasi.
  • Regresi linear sangat sensitif terhadap nilai-nilai yang tidak normal. Regresi linear sangat mempengaruhi regresi linear, dan akhirnya mempengaruhi nilai-nilai yang diprediksi.
  • Komoditas ganda akan meningkatkan diferensiasi dari perkiraan nilai koefisien, membuat perkiraan sangat sensitif terhadap perubahan kecil pada model. Hasilnya adalah bahwa perkiraan koefisien tidak stabil.
  • Dalam kasus dengan banyak variabel, kita dapat menggunakan metode forward selection, backward elimination, dan stepwise filtering untuk memilih variabel terpenting.

• Regressi Logistik 2.

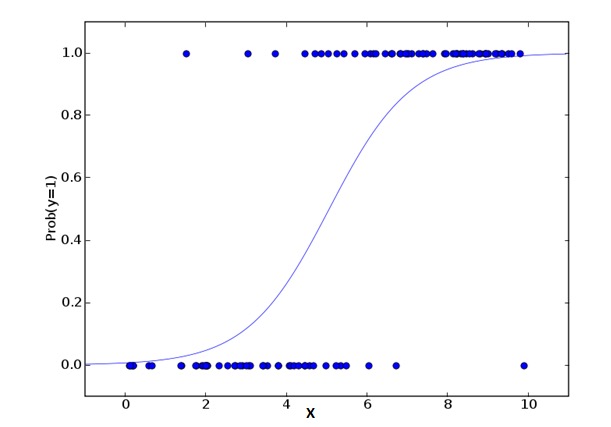
  Regresi logis digunakan untuk menghitung probabilitas dari event =Success dan event =Failure. Kita harus menggunakan regresi logis ketika tipe variabel adalah variabel biner ((¹⁄₀, true/false, yes/no). Di sini, nilai Y adalah dari 0 hingga 1, yang dapat dinyatakan dengan persamaan berikut:

  odds= p/ (1-p) = probability of event occurrence / probability of not event occurrence
  ln(odds) = ln(p/(1-p))
  logit(p) = ln(p/(1-p)) = b0+b1X1+b2X2+b3X3....+bkXk
  

  Dalam rumus di atas, p menyatakan probabilitas memiliki suatu sifat. Anda harus bertanya pertanyaan seperti ini: Mengapa kita menggunakan logaritma dalam rumus?

  Karena di sini kita menggunakan distribusi biner ((berdasarkan variabel), kita perlu memilih salah satu fungsi penyambung yang optimal untuk distribusi ini. Fungsi ini adalah fungsi Logit. Dalam persamaan di atas, parameter dipilih dengan mengamati sampel dengan sangat mirip dengan perkiraan nilai, bukan dengan meminimalkan kuadrat dan kesalahan (seperti yang digunakan dalam regresi biasa).

  

  Intinya:

  • Ini digunakan secara luas untuk masalah klasifikasi.
  • Regresi logis tidak memerlukan hubungan linier antara variabel dan variabel induk. Regresi logis dapat menangani berbagai jenis hubungan, karena menggunakan konversi log non-linier terhadap indeks risiko relatif yang diproyeksikan.
  • Untuk menghindari over fit dan under fit, kita harus memasukkan semua variabel penting. Ada cara yang bagus untuk memastikan hal ini adalah dengan menggunakan metode penyaringan bertahap untuk memperkirakan logical regression.
  • Ini membutuhkan jumlah sampel yang besar, karena dalam kasus jumlah sampel yang lebih kecil, kemungkinan besar perkiraan efeknya lebih buruk daripada minimal dua kali lipat biasa.
  • Variabel-variabel yang seharusnya tidak saling terkait, yaitu tidak memiliki banyak ko-linearitas. Namun, dalam analisis dan pemodelan, kita dapat memilih untuk memasukkan pengaruh interaksi variabel klasifikasi.
  • Jika nilai variabel akibat adalah variabel berurutan, maka disebut sebagai regresi logika berurutan.
  • Jika suatu variabel adalah multi-kategori, maka disebut sebagai multivariate logical regression.

• 3. Regressi Polinomial

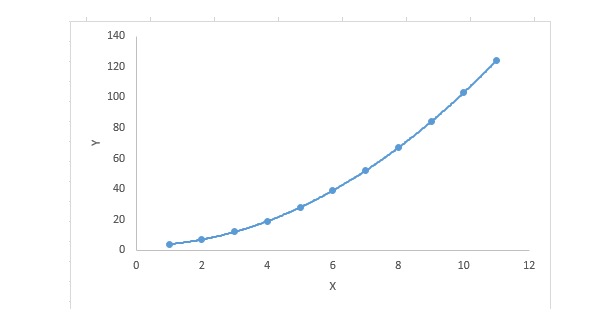
  Untuk suatu persamaan regresi, jika indeks dari variabel tersebut lebih besar dari 1, maka ia adalah persamaan regresi polinomial. Persamaan berikut ini ditunjukkan:

  y=a+b*x^2
  

  Dalam teknik regresi ini, garis yang paling cocok bukan garis lurus.

  

  Fokusnya:

  • Meskipun ada sebuah induksi yang dapat mencocokkan sebuah polinomial tingkat tinggi dan mendapatkan kesalahan yang lebih rendah, hal ini dapat menyebabkan overcocokan. Anda perlu sering-sering membuat diagram hubungan untuk melihat apakah ada yang cocok, dan fokuslah untuk memastikan bahwa cocoknya masuk akal, tidak ada yang terlalu cocok dan tidak ada yang kurang cocok. Berikut adalah diagram yang dapat membantu memahami:

  

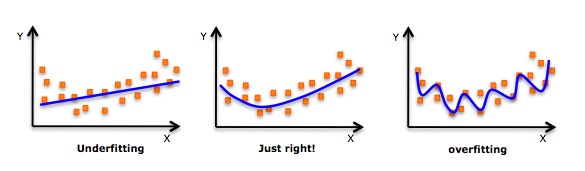
  • Carilah titik-titik kurva yang jelas di kedua ujungnya untuk melihat apakah bentuk dan tren ini masuk akal. Polimer tingkat yang lebih tinggi dapat menghasilkan kesimpulan yang aneh.

• 4. Regressi Langkah demi langkah

  Dalam teknik ini, pilihan variabel otomatis dilakukan dalam proses otomatis, yang mencakup operasi non-manusia.

  Perbuatan ini dilakukan dengan mengamati nilai-nilai statistik, seperti R-square, t-stats, dan AIC, untuk mengidentifikasi variabel-variabel penting. Regresi bertahap menyesuaikan model dengan menambahkan/menghapus ko-variabel berdasarkan kriteria yang ditentukan secara bersamaan. Berikut adalah beberapa metode regresi bertahap yang paling umum digunakan:

  • Regressi bertahap standar melakukan dua hal: menambah dan mengurangi prediksi yang dibutuhkan untuk setiap langkah.
  • Pemilihan ke depan dimulai dengan prediksi yang paling menonjol dari model, dan kemudian menambahkan variabel untuk setiap langkah.
  • Penghapusan backscatter dimulai pada saat yang sama dengan semua prediksi model, kemudian menghapus variabel yang paling tidak signifikan pada setiap langkah.
  • Teknik pemodelan ini bertujuan untuk memaksimalkan kemampuan prediksi dengan menggunakan jumlah variabel prediksi yang paling sedikit. Ini juga merupakan salah satu metode untuk menangani dataset berdimensi tinggi.

• 5. Regressi Ridge

  Analisis regresi berlian adalah teknik yang digunakan untuk data yang memiliki banyak ko-linearitas. Dalam banyaknya ko-linearitas, meskipun penggandaan minimal (OLS) berlaku adil untuk setiap variabel, perbedaan mereka sangat besar sehingga nilai pengamatan menyimpang dan jauh dari nilai sebenarnya. Regresi berlian mengurangi kesalahan standar dengan menambahkan satu bias pada estimasi regresi.

  Di atas, kita melihat persamaan regresi linier. Ingat?

  y=a+ b*x
  

  Persamaan ini juga memiliki nilai kesalahan. Persamaan lengkapnya adalah:

  y=a+b*x+e (error term),  [error term is the value needed to correct for a prediction error between the observed and predicted value]
  => y=a+y= a+ b1x1+ b2x2+....+e, for multiple independent variables.
  

  Dalam persamaan linear, kesalahan prediksi dapat dipecah menjadi dua subpartikel. Salah satunya adalah deviasi dan yang lainnya adalah diferensial. Kesalahan prediksi dapat disebabkan oleh kedua faktor ini atau salah satu dari keduanya.

  Regressi lambda memecahkan masalah komoditas ganda dengan menggunakan parameter kompresi λ ((lambda)). Lihat rumus di bawah

  

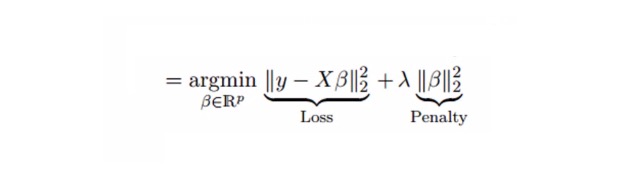
  Dalam rumus ini, ada dua komponen. Yang pertama adalah binomial terkecil, dan yang lainnya adalah kelipatan λ dari β2 ((β-squared), di mana β adalah koefisien terkait. Untuk mempersingkat parameter, tambahkan ke binomial terkecil untuk mendapatkan diferensial yang sangat rendah.

  Intinya:

  • Regresi ini mirip dengan Regresi Minimal Dua Kali, kecuali untuk konstanta.
  • Ini menyusut nilai dari koefisien terkait, tetapi tidak mencapai nol, yang menunjukkan bahwa ia tidak memiliki fitur pilihan
  • Ini adalah metode regulalisasi dan menggunakan regulalisasi L2.

• 6. Regressi Lasso

  Ini mirip dengan regressi berlian, Lasso (Least Absolute Shrinkage and Selection Operator) juga akan menghukum ukuran mutlak dari faktor regressi. Selain itu, ini dapat mengurangi tingkat perubahan dan meningkatkan akurasi model regressi linier. Lihat rumus berikut:

  

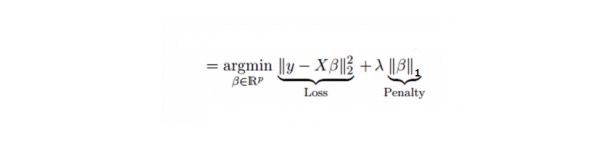
  Regressi Lasso sedikit berbeda dengan Regressi Ridge, yang menggunakan fungsi hukuman sebagai nilai absolut, bukan kuadrat. Hal ini menyebabkan hukuman (atau sama dengan jumlah nilai absolut dari perkiraan yang dibatasi) membuat beberapa hasil perkiraan parameter sama dengan nol.

  Intinya:

  • Regresi ini mirip dengan Regresi Minimal Dua Kali, kecuali untuk konstanta.
  • Koefisien kontraksi mendekati nol (<=0), yang memang membantu dalam pemilihan karakteristik;
  • Ini adalah metode regulasi, yang menggunakan regulasi L1;
  • Jika satu set variabel yang diprediksi sangat relevan, Lasso akan memilih salah satu dari mereka dan mengurangi yang lain menjadi nol.

• 7. Kembali ke ElasticNet

  ElasticNet adalah hibrida dari teknik Lasso dan Ridge Regression. ElasticNet menggunakan L1 untuk melatih dan L2 diutamakan sebagai matriks normalisasi. ElasticNet sangat berguna ketika ada beberapa karakteristik yang terkait.

  

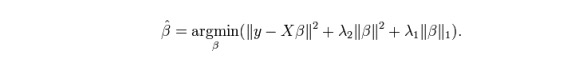
  Kelebihan praktis antara Lasso dan Ridge adalah bahwa hal itu memungkinkan ElasticNet mewarisi beberapa stabilitas Ridge dalam keadaan lingkaran.

  Intinya:

  • Dalam kasus variabel yang sangat terkait, ini akan menghasilkan efek kelompok.
  • Tidak ada batasan jumlah variabel yang dapat dipilih.
  • Ini bisa menahan double-compression.
  • Selain 7 teknik regresi yang paling umum digunakan, Anda juga dapat melihat model lain seperti regresi Bayesian, Ekologis, dan Robust.

• Bagaimana memilih model regresi yang tepat?

  Hidup seringkali lebih mudah ketika Anda hanya tahu satu atau dua teknik. Saya tahu satu lembaga pelatihan yang mengatakan kepada siswa mereka bahwa jika hasilnya kontinu, gunakan regresi linier. Jika biner, gunakan regresi logis! Namun, dalam pemrosesan kita, semakin banyak pilihan yang tersedia, semakin sulit untuk memilih yang benar.

  Dalam model regresi multi-kategori, sangat penting untuk memilih teknik yang paling sesuai berdasarkan pada jenis variabel dan faktor variabel, dimensi data, dan karakteristik dasar lainnya dari data. Berikut adalah faktor-faktor kunci untuk memilih model regresi yang benar:

  Eksplorasi data adalah bagian penting dari model prediksi. Ini harus menjadi langkah utama dalam memilih model yang tepat, seperti mengidentifikasi hubungan dan pengaruh variabel.

  Perbandingan yang lebih cocok untuk model yang berbeda, kita dapat menganalisis parameter indikator yang berbeda, seperti parameter yang signifikan secara statistik, R-square, Adjusted R-square, AIC, BIC, dan titik kesalahan, dan yang lain adalah Mallows’ Cp rule. Ini terutama dilakukan dengan membandingkan model dengan semua submodel yang mungkin (atau memilih mereka dengan hati-hati), memeriksa kemungkinan bias dalam model Anda.

  Cross-validation adalah cara terbaik untuk mengevaluasi model prediksi. Di sini, membagi dataset Anda menjadi dua bagian (satu untuk latihan dan satu untuk verifikasi). Menggunakan perbedaan rata-rata sederhana antara nilai pengamatan dan nilai prediksi untuk mengukur akurasi prediksi Anda.

  Jika dataset Anda adalah beberapa variabel campuran, maka Anda tidak harus memilih metode pilihan model otomatis, karena Anda tidak ingin menempatkan semua variabel dalam model yang sama pada waktu yang sama.

  Ini juga tergantung pada tujuan Anda. Mungkin ada situasi di mana model yang kurang kuat lebih mudah diterapkan dibandingkan dengan model yang memiliki signifikansi statistik yang tinggi.

  Metode Regression Normalization ((Lasso, Ridge dan ElasticNet) bekerja dengan baik dalam situasi ko-linearitas ganda antara variabel dataset berdimensi tinggi.

Diposting oleh CSDN