Pemahaman Menarik tentang Naive Bayes

NavieBayes

  Banyak situasi dalam kehidupan yang membutuhkan klasifikasi, seperti klasifikasi berita, klasifikasi pasien, dan lain-lain. Untuk membuat Anda dapat memahami gambaran, artikel ini memperkenalkan sebuah algoritma klasifikasi sederhana yang umum digunakan mulai dari aplikasi praktis - Bayes polos (Navie Bayes classifier).

• 01 Contoh klasifikasi pasien

Mari saya mulai dengan sebuah contoh, Anda akan melihat bahwa klasifikasi Bayesian sangat mudah dipahami, tidak sulit.

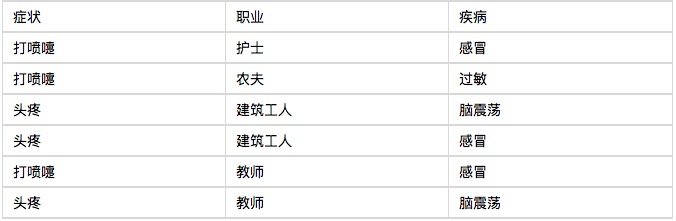
Sekarang datang pasien ketujuh, seorang pekerja konstruksi yang bersin. Tanyakan berapa besar kemungkinan dia terkena flu?

  P(A|B) = P(B|A) P(A) / P(B)

Mungkin:

  P(感冒|打喷嚏x建筑工人) 
  　　　　= P(打喷嚏x建筑工人|感冒) x P(感冒) 
  　　　　/ P(打喷嚏x建筑工人)

Dengan asumsi bahwa sifat-sifat “menghisap” dan “pekerja konstruksi” adalah sifat-sifat yang terpisah, maka persamaan di atas menjadi

  P(感冒|打喷嚏x建筑工人) 
  　　　　= P(打喷嚏|感冒) x P(建筑工人|感冒) x P(感冒)
  　　　　/ P(打喷嚏) x P(建筑工人)

Ini bisa dihitung.

  P(感冒|打喷嚏x建筑工人) 
  　　　　= 0.66 x 0.33 x 0.5 / 0.5 x 0.33 
  　　　　= 0.66

Oleh karena itu, seorang pekerja bangunan yang bersin memiliki kemungkinan 66% terkena flu. Dengan cara yang sama, Anda dapat menghitung kemungkinan pasien mengalami alergi atau kejang. Dengan membandingkan probabilitas ini, Anda dapat mengetahui penyakit apa yang paling mungkin dia alami.

Ini adalah metode dasar dari klasifikasi Bayesian: berdasarkan data statistik, berdasarkan karakteristik tertentu, perhitungan probabilitas dari setiap kategori, untuk mencapai klasifikasi.

• 02 Rumus dari klasifikasi Bayesian sederhana

Asumsikan bahwa suatu individu memiliki n karakteristik, masing-masing F1, F2, … , Fn. Ada m kategori, masing-masing C1, C2, … , Cm. Klasifikasi Bayesian adalah klasifikasi yang menghitung probabilitas terbesar, yaitu nilai maksimum dari rumus berikut:

  P(C|F1F2...Fn) 
  　　   = P(F1F2...Fn|C)P(C) / P(F1F2...Fn)

Karena P ((F1F2…Fn) adalah sama untuk semua kategori, dapat dihapus, dan pertanyaannya berubah menjadi mencari

  P(F1F2...Fn|C)P(C)

Nilai maksimum

Klasifikator Bayesian yang sederhana lebih jauh lagi, dengan asumsi bahwa semua karakteristik bersifat independen dari satu sama lain, dan karenanya

  P(F1F2...Fn|C)P(C) 
  　　   = P(F1|C)P(F2|C) ... P(Fn|C)P(C)

Setiap elemen di sebelah kanan persamaan dapat diperoleh dari data statistik, dan dengan demikian dapat dihitung probabilitas dari masing-masing kategori yang sesuai, sehingga menemukan kategori dengan probabilitas terbesar.

Meskipun hipotesis “semua karakteristik saling independen” tidak mungkin berlaku dalam realitas, itu dapat sangat menyederhanakan perhitungan, dan penelitian menunjukkan bahwa itu tidak mempengaruhi akurasi hasil klasifikasi.

Berikut ini adalah dua contoh tentang bagaimana menggunakan klasifikasi Bayesian sederhana.

• 03 Klasifikasi akun

Berdasarkan sampel dari sebuah situs komunitas, 89% dari 10.000 akun di situs tersebut adalah akun asli (setel C0) dan 11% adalah akun palsu (setel C1).

  C0 = 0.89 C1 = 0.11

Anggaplah sebuah akun memiliki tiga karakteristik berikut: F1: Jumlah jurnal/hari pendaftaran F2: Jumlah teman/hari pendaftaran F3: Apakah menggunakan headset asli (headset asli adalah 1, headset non-real adalah 0) F1 = 0.1  F2 = 0.2  F3 = 0

Pertanyaan: Apakah akun tersebut asli atau palsu? Cara yang digunakan adalah dengan menggunakan klasifikasi Bayesian sederhana dan menghitung nilai dari rumus berikut:

P(F1|C)P(F2|C)P(F3|C)P©

Meskipun nilai-nilai di atas dapat diperoleh dari statistik, namun ada masalah di sini: F1 dan F2 adalah variabel berturut-turut, dan tidak cocok untuk menghitung probabilitas berdasarkan nilai tertentu.[0, 0.05]、(0.05, 0.2)、[0.2, +∞] tiga interval, lalu hitung probabilitas dari setiap interval. Dalam contoh kita, F1 = 0.1, jatuh di interval kedua, jadi hitunglah probabilitas dari interval kedua.

Menurut statistik, ada:

P(F1|C0) = 0.5, P(F1|C1) = 0.1  P(F2|C0) = 0.7, P(F2|C1) = 0.2  P(F3|C0) = 0.2, P(F3|C1) = 0.9

Oleh karena itu

P(F1|C0) P(F2|C0) P(F3|C0) P(C0)  = 0.5 x 0.7 x 0.2 x 0.89  = 0.0623 P(F1|C1) P(F2|C1) P(F3|C1) P(C1)  = 0.1 x 0.2 x 0.9 x 0.11  = 0.00198 Anda dapat melihat bahwa meskipun pengguna ini tidak menggunakan foto aslinya, kemungkinan akunnya asli lebih dari 30 kali lebih tinggi daripada akun palsu, sehingga akun ini dianggap asli.

• 04 Klasifikasi gender

Berikut ini adalah statistik dari beberapa karakteristik tubuh manusia.

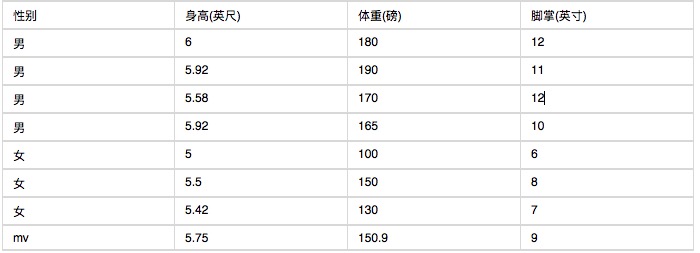
Jika seseorang diketahui setinggi 6 kaki, berat 130 pon, telapak kaki 8 inci, apakah orang tersebut laki-laki atau perempuan?

P ((Tinggi tubuh dan jenis kelamin) x P ((Bobot dan jenis kelamin) x P ((Tangan dan jenis kelamin) x P ((Jinis)

Masalahnya adalah, karena tinggi badan, berat badan, dan telapak kaki adalah variabel berturut-turut, maka tidak mungkin untuk menghitung probabilitas dengan menggunakan metode variabel terpisah. Dan karena jumlah sampel terlalu sedikit, maka tidak mungkin untuk menghitung interval. Apa yang harus dilakukan? Anda dapat mengasumsikan bahwa tinggi badan, berat badan, dan telapak kaki pria dan wanita adalah distribusi normal.

Dengan data ini, kita dapat menghitung klasifikasi berdasarkan jenis kelamin.

P (tinggi = 6 orang dewasa) x P (berat = 130 orang dewasa) x P (tangan = 8 orang dewasa) x P (pria)

= 6.1984 x e-9

P (tinggi = 6 orang dewasa) x P (berat = 130 orang dewasa) x P (tangan = 8 orang dewasa) x P (wanita)

= 5.3778 x e-4

Seperti yang Anda lihat, wanita memiliki kemungkinan hampir 10.000 kali lebih besar untuk menjadi wanita daripada pria, jadi orang tersebut adalah wanita.

WeChat Public Number yang diunggah dari Gunung Fuji