Model Markov Tersembunyi

• ### Pertama, mengenal

Hari ini kita akan membahas tentang aplikasi sederhana dari HMM dalam saham.

Model Markov Hidden, yang kedengarannya sangat canggih, tidak tahu apa-apa, jadi mari kita mundur dan melihat rantai Markov.

Rantai Markov, yang diberi nama oleh Andrei Markov (A.A. Markov, 1856-1922) adalah proses acak peristiwa terpisah yang bersifat Markovik dalam matematika. Dalam konteks pengetahuan atau informasi saat ini, masa lalu (yaitu, keadaan sejarah sebelum saat ini) tidak relevan untuk memprediksi masa depan (yaitu, keadaan masa depan setelah saat ini).

Dalam proses ini, perpindahan setiap keadaan hanya bergantung pada n keadaan sebelumnya, proses ini disebut model dengan 1 n pangkat, di mana n adalah jumlah pengaruh dari perpindahan keadaan. Proses Markov yang paling sederhana adalah proses satu pangkat, di mana perpindahan setiap keadaan hanya bergantung pada keadaan sebelumnya.

• ### Kedua, contoh

Dalam bentuk matematis, ini adalah sebagai berikut:

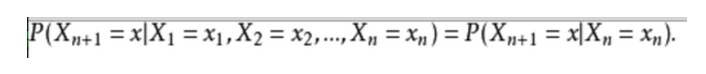
Sebagai contoh dari kehidupan sehari-hari, kita ingin memprediksi kondisi cuaca di masa depan berdasarkan kondisi cuaca saat ini. Salah satu cara adalah dengan mengasumsikan bahwa setiap kondisi dari model ini hanya bergantung pada kondisi yang sebelumnya, yaitu hipotesis Markov, yang sangat menyederhanakan masalah ini. Tentu saja, contoh ini juga tidak praktis. Namun, sistem yang disederhanakan seperti itu dapat membantu analisis kita, jadi kita biasanya menerima hipotesis seperti itu karena kita tahu bahwa sistem seperti itu dapat memberi kita beberapa informasi yang berguna, meskipun tidak terlalu akurat.

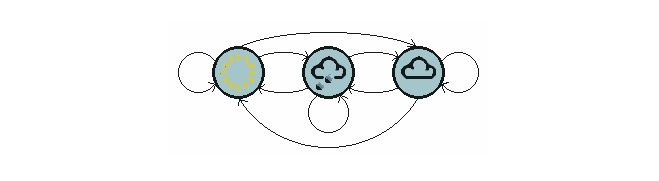
Grafik di atas menunjukkan model perpindahan cuaca.

Perhatikan bahwa proses satu tingkat dengan N keadaan memiliki N 2 pergeseran keadaan. Setiap kemungkinan pergeseran disebut probabilitas pergeseran keadaan, yaitu probabilitas pergeseran dari satu keadaan ke keadaan lain. Semua N 2 kemungkinan ini dapat diwakili dengan matriks pergeseran keadaan, seperti dalam contoh cuaca di atas:

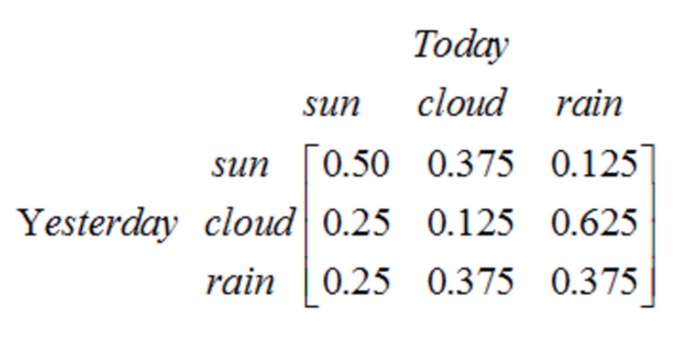
Matriks ini menyatakan bahwa jika kemarin adalah hari yang berawan, maka hari ini memiliki probabilitas 25% bahwa hari itu cerah, 12.5% probabilitas bahwa hari itu berawan, dan 62.5% probabilitas bahwa akan turun hujan.

Untuk menginisialisasi sistem seperti itu, kita membutuhkan sebuah vektor probabilitas awal:

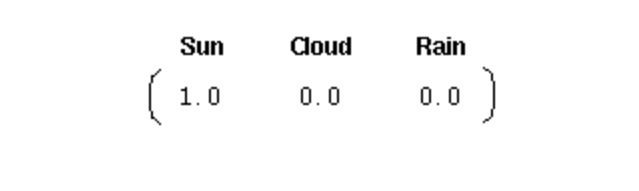
Vektor ini menunjukkan bahwa hari pertama adalah hari yang cerah. Di sini, kita mendefinisikan tiga bagian berikut untuk proses Markov satu tingkat di atas:

Status: cerah, mendung dan hujan.

Vektor awal: Probabilitas dari keadaan sistem pada waktu 0.

Matriks perpindahan keadaan: probabilitas setiap perubahan cuaca. Semua sistem yang dapat digambarkan dengan cara ini adalah proses Markov.

Namun, apa yang harus kita lakukan ketika proses Markov tidak cukup kuat? Dalam beberapa kasus, proses Markov tidak cukup untuk menggambarkan pola yang kita ingin temukan.

Sebagai contoh, jika kita hanya mengamati pasar saham, kita hanya bisa mengetahui informasi tentang harga, volume transaksi, dan lain-lain pada hari itu, tetapi tidak tahu apa kondisi pasar saham saat ini (bull market, bear market, shock market, rebound market, dan lain-lain), dalam hal ini kita memiliki dua set keadaan, satu set keadaan yang dapat diamati (stock market price trading state, dan lain-lain) dan satu set keadaan yang tersembunyi (stock market condition). Kita berharap untuk menemukan sebuah algoritma yang dapat memprediksi kondisi pasar saham berdasarkan kondisi harga dan volume transaksi pasar saham dan hipotesis Markov.

Dalam kasus-kasus di atas, urutan keadaan yang dapat diamati dan urutan keadaan yang tersembunyi adalah probabilitas terkait. Oleh karena itu, kita dapat memodelkan jenis proses ini sebagai sebuah proses Markov tersembunyi dan sebuah set keadaan yang terkait dengan probabilitas proses Markov tersembunyi dan dapat diamati, yaitu model Markov tersembunyi.

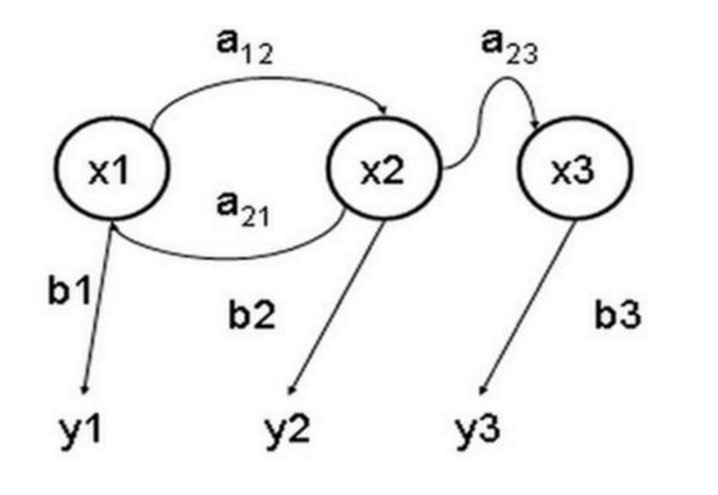
Hidden Markov Model adalah sebuah model statistik yang digunakan untuk menggambarkan suatu proses Markov yang mengandung parameter tersembunyi yang tidak diketahui. Hal yang sulit dilakukan adalah menentukan parameter tersembunyi dari proses tersebut dari parameter yang dapat diamati, dan kemudian menggunakan parameter tersebut untuk melakukan analisis lebih lanjut. Gambar di bawah ini adalah peta transisi state dari model Markov tersembunyi dalam tiga keadaan, di mana x mewakili keadaan tersembunyi, y mewakili hasil yang dapat diamati, a mewakili probabilitas konversi keadaan, dan b mewakili probabilitas hasil yang dihasilkan.

Misalkan saya memiliki tiga kalung yang berbeda. Kalung pertama adalah kalung biasa kita (sebutkan kalung ini sebagai D6), dengan 6 sisi, setiap sisi (sebutkan kalung ini sebagai D4), dan kemungkinan munculnya adalah ¹⁄₆. Kalung kedua adalah kalung empat sisi (sebutkan kalung ini sebagai D4), dan kemungkinan munculnya setiap sisi (sebutkan kalung ini sebagai D4) adalah ¹⁄₄. Kalung ketiga memiliki delapan sisi (sebutkan kalung ini sebagai D8), dan kemungkinan munculnya setiap sisi (sebutkan kalung ini sebagai D8) adalah ¹⁄₈.

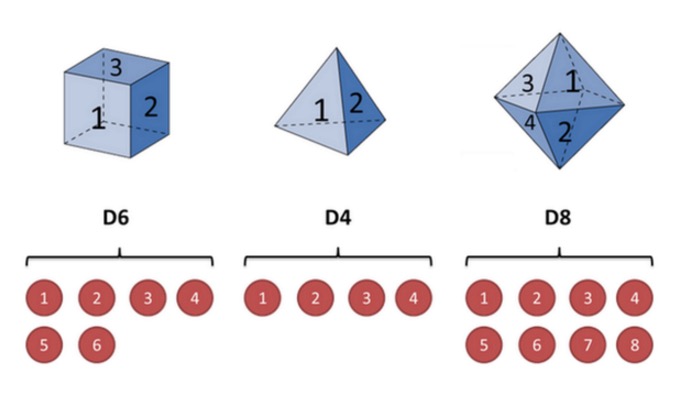
Misalkan kita mulai dengan mengoleskan, kita pilih satu dari tiga kotak, dan setiap kotak memiliki probabilitas ¹⁄₃. Kemudian kita mengoleskan, dan kita mendapatkan satu angka, 1, 2, 3, 4, 5, 6, 7, 8. Berulang-ulang proses di atas, kita akan mendapatkan serangkaian angka, dan setiap angka adalah salah satu dari 1, 2, 3, 4, 5, 6, 7, 8.

Garis angka ini disebut rantai keadaan yang terlihat. Tetapi dalam model Markov tersirat, kita tidak hanya memiliki rantai keadaan yang terlihat, kita juga memiliki rantai keadaan tersirat. Dalam contoh ini, rantai keadaan tersirat adalah urutan yang Anda gunakan. Sebagai contoh, rantai keadaan tersirat mungkin: D4 D6 D8 D6 D4 D8 D6 D6 D4

Secara umum, rantai Markov yang disebutkan dalam HMM sebenarnya adalah rantai keadaan tersembunyi, karena ada probabilitas konversi antara keadaan tersembunyi ((kucing)). Dalam contoh kita, keadaan berikutnya dari D6 adalah D4, D6, D8 memiliki probabilitas 1 / 3. D4, D8, keadaan berikutnya adalah D4, D6, D8 juga memiliki probabilitas konversi 1 / 3.

Demikian pula, meskipun tidak ada probabilitas konversi antara keadaan yang terlihat, ada probabilitas antara keadaan yang tersirat dan keadaan yang terlihat yang disebut probabilitas output. Dalam contoh kita, kotak enam sisi (D6) menghasilkan 1 dengan probabilitas output ¹⁄₆. Kita juga dapat membuat definisi lain tentang probabilitas output.

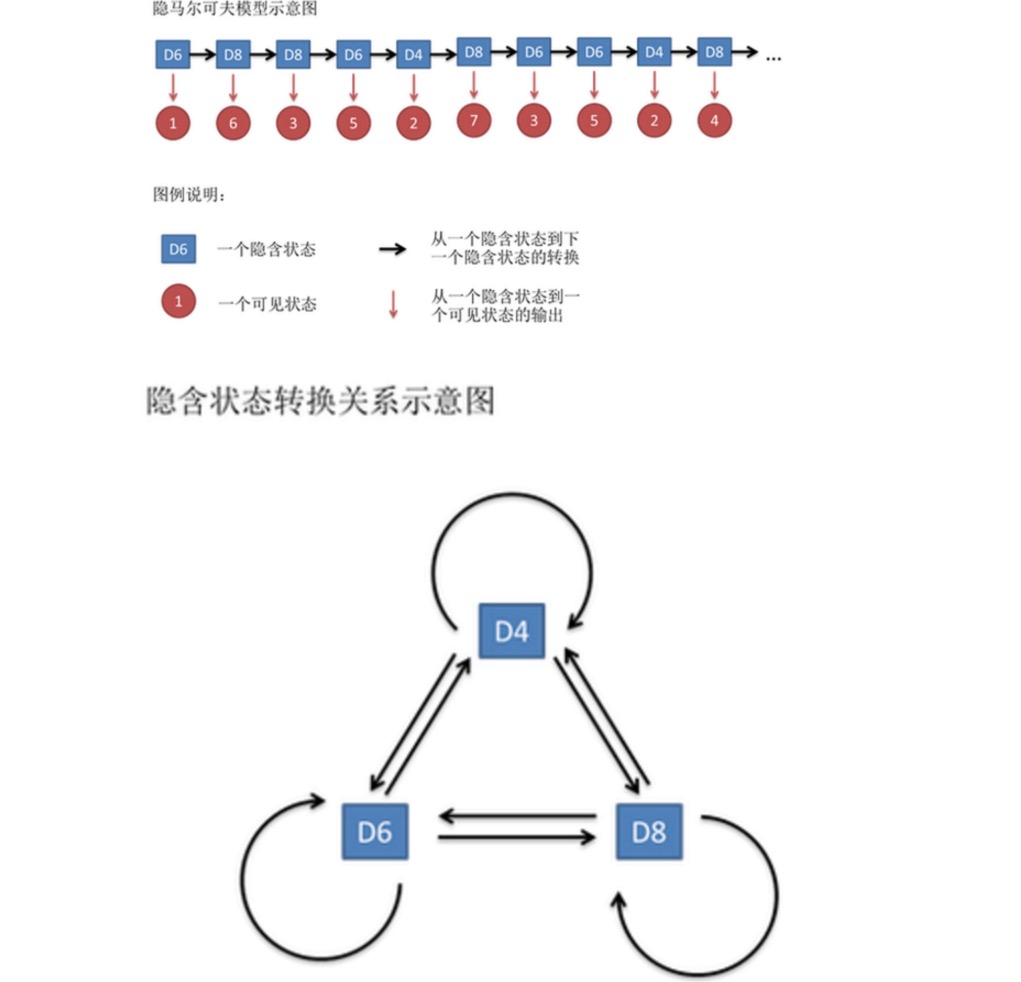
Sebenarnya untuk HMM, melakukan simulasi cukup mudah jika Anda tahu sebelumnya probabilitas konversi antara semua keadaan tersembunyi dan probabilitas output antara semua keadaan tersembunyi ke semua keadaan yang terlihat. Tetapi ketika menerapkan model HMM, seringkali ada beberapa informasi yang hilang, kadang-kadang Anda tahu berapa banyak kerucut, apa yang ada di setiap kerucut, tetapi tidak tahu urutan kerucut yang keluar; kadang-kadang Anda hanya melihat hasil kerucut berkali-kali, dan tidak tahu apa-apa sisanya. Jika Anda menerapkan algoritma untuk memperkirakan informasi yang hilang, itu menjadi masalah yang sangat penting.

Algoritma yang terkait dengan model HMM dibagi menjadi tiga kategori, masing-masing untuk memecahkan tiga jenis masalah:

• Saya ingin tahu berapa banyak jenis keong yang ada (jumlah keadaan tersirat), apa setiap jenis keong (probabilitas konversi), berdasarkan hasil yang dikeluarkan oleh keong (rantai keadaan yang terlihat), saya ingin tahu keong apa yang dikeluarkan setiap kali (rantai keadaan tersirat).

• Saya juga ingin tahu berapa banyak jenis kepiting yang ada, berapa banyak keadaan yang terpendam, berapa probabilitas setiap jenis kepiting, dan berapa probabilitas untuk mendapatkan hasil ini berdasarkan hasil kepiting.

• Mengetahui berapa banyak kerucut yang ada (jumlah keadaan tersirat), tidak tahu apa setiap jenis kerucut (probabilitas konversi), mengamati hasil dari banyak kerucut (rantai keadaan yang terlihat), saya ingin menyimpulkan apa setiap jenis kerucut (probabilitas konversi).

  Jika kita ingin menyelesaikan masalah di pasar saham di atas, kita perlu menyelesaikan masalah 1 dan masalah 3, dan di artikel berikutnya kita akan melihat bagaimana kita bisa melakukannya.

Dikutip dari Moneycode