Pemikiran tentang strategi perdagangan frekuensi tinggi (2)
 1
1
 3416
3416
Artikel ini terutama membahas strategi perdagangan frekuensi tinggi, dengan fokus pada pemodelan volume kumulatif dan guncangan harga. Makalah ini mengusulkan model penempatan pesanan optimal awal dengan menganalisis dampak transaksi tunggal, guncangan harga interval tetap, dan volume transaksi terhadap harga. Model ini mencoba menemukan posisi perdagangan optimal berdasarkan pemahaman guncangan volume dan harga. Asumsi model dibahas secara mendalam, dan penilaian awal tentang penempatan pesanan optimal dilakukan dengan membandingkan pengembalian aktual dan pengembalian yang diharapkan berdasarkan prediksi model.
Pemodelan Volume Kumulatif
Artikel sebelumnya memberikan ekspresi probabilitas untuk volume transaksi tunggal yang lebih besar dari nilai tertentu:
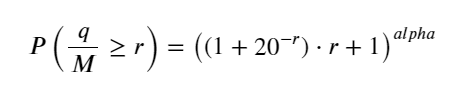
Kami juga memperhatikan distribusi volume perdagangan selama periode waktu tertentu, yang secara intuitif seharusnya terkait dengan volume setiap transaksi dan frekuensi pesanan. Berikutnya, data diproses pada interval tertentu. Gambarkan distribusinya seperti di atas.
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
trades = pd.read_csv('HOOKUSDT-aggTrades-2023-01-27.csv')
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
buy_trades.index = buy_trades['date']
Gabungkan volume transaksi setiap 1s, hapus bagian yang tidak terjadi transaksi, dan gunakan distribusi transaksi tunggal di atas untuk menyesuaikan. Dapat dilihat bahwa hasilnya lebih baik. Jika semua transaksi dalam 1s dianggap sebagai transaksi tunggal, masalah ini menjadi Ini telah menjadi masalah yang terpecahkan. Namun, ketika siklus diperpanjang (relatif terhadap frekuensi transaksi), kesalahan ditemukan meningkat, dan penelitian telah menemukan bahwa kesalahan ini disebabkan oleh istilah koreksi distribusi Pareto sebelumnya. Artinya, seiring siklus bertambah panjang dan mencakup lebih banyak transaksi individual, kombinasi beberapa transaksi mendekati distribusi Pareto. Dalam kasus ini, istilah koreksi harus dihilangkan.
df_resampled = buy_trades['quantity'].resample('1S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
buy_trades
| agg_trade_id | price | quantity | first_trade_id | last_trade_id | is_buyer_maker | date | transact_time | interval | diff | |
|---|---|---|---|---|---|---|---|---|---|---|
| 2023-01-27 00:00:00.161 | 1138369 | 2.901 | 54.3 | 3806199 | 3806201 | False | 2023-01-27 00:00:00.161 | 1674777600161 | NaN | 0.001 |
| 2023-01-27 00:00:04.140 | 1138370 | 2.901 | 291.3 | 3806202 | 3806203 | False | 2023-01-27 00:00:04.140 | 1674777604140 | 3979.0 | 0.000 |
| 2023-01-27 00:00:04.339 | 1138373 | 2.902 | 55.1 | 3806205 | 3806207 | False | 2023-01-27 00:00:04.339 | 1674777604339 | 199.0 | 0.001 |
| 2023-01-27 00:00:04.772 | 1138374 | 2.902 | 1032.7 | 3806208 | 3806223 | False | 2023-01-27 00:00:04.772 | 1674777604772 | 433.0 | 0.000 |
| 2023-01-27 00:00:05.562 | 1138375 | 2.901 | 3.5 | 3806224 | 3806224 | False | 2023-01-27 00:00:05.562 | 1674777605562 | 790.0 | 0.000 |
| … | … | … | … | … | … | … | … | … | … | … |
| 2023-01-27 23:59:57.739 | 1544370 | 3.572 | 394.8 | 5074645 | 5074651 | False | 2023-01-27 23:59:57.739 | 1674863997739 | 1224.0 | 0.002 |
| 2023-01-27 23:59:57.902 | 1544372 | 3.573 | 177.6 | 5074652 | 5074655 | False | 2023-01-27 23:59:57.902 | 1674863997902 | 163.0 | 0.001 |
| 2023-01-27 23:59:58.107 | 1544373 | 3.573 | 139.8 | 5074656 | 5074656 | False | 2023-01-27 23:59:58.107 | 1674863998107 | 205.0 | 0.000 |
| 2023-01-27 23:59:58.302 | 1544374 | 3.573 | 60.5 | 5074657 | 5074657 | False | 2023-01-27 23:59:58.302 | 1674863998302 | 195.0 | 0.000 |
| 2023-01-27 23:59:59.894 | 1544376 | 3.571 | 12.1 | 5074662 | 5074664 | False | 2023-01-27 23:59:59.894 | 1674863999894 | 1592.0 | 0.000 |
#1s内的累计分布
depths = np.array(range(0, 3000, 5))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
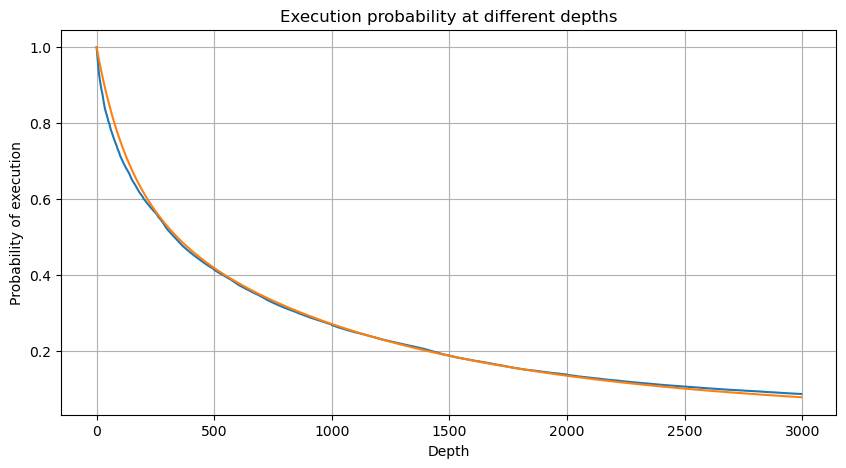
df_resampled = buy_trades['quantity'].resample('30S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 12000, 20))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2)
probabilities_s_2 = np.array([(depth/mean+1)**alpha for depth in depths]) # 无修正
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities,label='Probabilities (True)')
plt.plot(depths, probabilities_s, label='Probabilities (Simulation 1)')
plt.plot(depths, probabilities_s_2, label='Probabilities (Simulation 2)')
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.legend()
plt.grid(True)
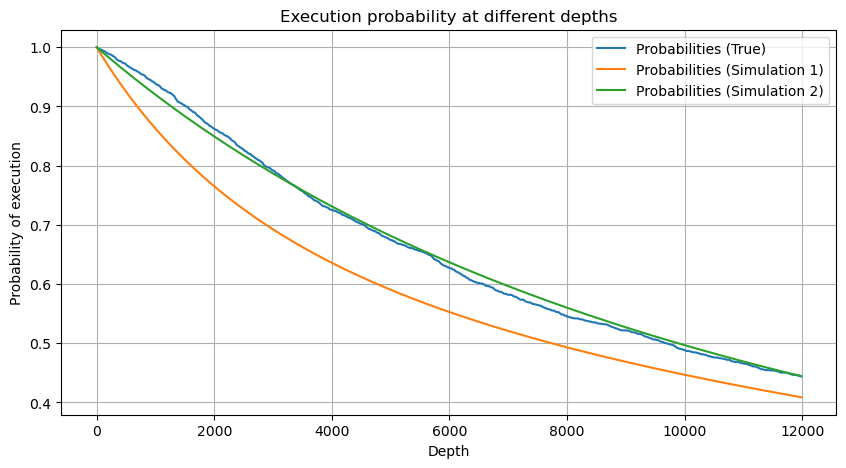
Sekarang kami telah meringkas rumus umum untuk distribusi volume perdagangan terakumulasi pada waktu yang berbeda, dan menggunakan distribusi transaksi tunggal untuk menyesuaikannya, alih-alih menghitungnya secara terpisah setiap waktu. Di sini kita abaikan prosesnya dan langsung berikan rumusnya:
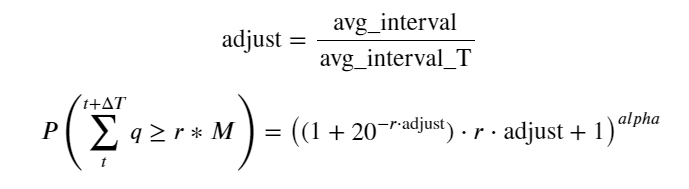
Di antara mereka, avg_interval mewakili interval rata-rata antara transaksi tunggal, dan avg_interval_T mewakili interval rata-rata dari interval yang perlu diestimasi. Agak membingungkan. Jika kita ingin memperkirakan waktu transaksi 1 detik, kita perlu menghitung interval rata-rata antara peristiwa yang berisi transaksi dalam 1 detik. Jika probabilitas kedatangan suatu pesanan sesuai dengan distribusi Poisson, maka seharusnya mungkin untuk memperkirakannya secara langsung di sini, tetapi deviasi aktualnya besar, jadi saya tidak akan menjelaskannya di sini.
Perlu diperhatikan bahwa probabilitas volume yang lebih besar dari nilai tertentu dalam interval tertentu harus sangat berbeda dari probabilitas aktual transaksi pada posisi kedalaman tersebut, karena semakin lama waktu tunggu, semakin besar kemungkinan buku pesanan berubah, dan transaksi juga mengarah ke Perubahan kedalaman, sehingga probabilitas transaksi pada posisi kedalaman yang sama berubah secara real time saat data diperbarui.
df_resampled = buy_trades['quantity'].resample('2S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 6500, 10))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = buy_trades['quantity'].mean()
adjust = buy_trades['interval'].mean() / 2620
alpha = np.log(np.mean(buy_trades['quantity'] > mean))/0.7178397931503168
probabilities_s = np.array([((1+20**(-depth*adjust/mean))*depth*adjust/mean+1)**(alpha) for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
Dampak harga transaksi tunggal
Data transaksi adalah harta karun, dan masih banyak sekali data yang bisa ditambang. Kita harus memerhatikan dengan seksama dampak order terhadap harga, yang memengaruhi penempatan order tertunda dalam strategi. Demikian pula, berdasarkan data agregat transact_time, hitung selisih antara harga terakhir dan harga pertama. Jika hanya ada satu pesanan, selisihnya adalah 0. Anehnya, masih ada sejumlah kecil hasil data dengan hasil negatif. Ini seharusnya menjadi masalah pada urutan penyusunan data, jadi saya tidak akan membahasnya di sini.
Hasil penelitian menunjukkan bahwa proporsi tidak ada dampak sebesar 77%, proporsi 1 tick sebesar 16,5%, 2 tick sebesar 3,7%, 3 tick sebesar 1,2%, dan proporsi lebih dari 4 tick kurang dari 1%. . Hal ini pada dasarnya sesuai dengan karakteristik fungsi eksponensial, tetapi penyesuaiannya tidak akurat.
Volume transaksi yang menyebabkan perbedaan harga yang sesuai dihitung, dan distorsi yang disebabkan oleh dampak yang terlalu besar dihilangkan. Hal ini pada dasarnya sesuai dengan hubungan linier, dan sekitar setiap 1.000 volume menyebabkan fluktuasi harga sebesar 1 tick. Dapat juga dipahami bahwa jumlah rata-rata pesanan tertunda di dekat setiap harga adalah sekitar 1.000.
diff_df = trades[trades['is_buyer_maker']==False].groupby('transact_time')['price'].agg(lambda x: abs(round(x.iloc[-1] - x.iloc[0],3)) if len(x) > 1 else 0)
buy_trades['diff'] = buy_trades['transact_time'].map(diff_df)
diff_counts = buy_trades['diff'].value_counts()
diff_counts[diff_counts>10]/diff_counts.sum()
0.000 0.769965
0.001 0.165527
0.002 0.037826
0.003 0.012546
0.004 0.005986
0.005 0.003173
0.006 0.001964
0.007 0.001036
0.008 0.000795
0.009 0.000474
0.010 0.000227
0.011 0.000187
0.012 0.000087
0.013 0.000080
Name: diff, dtype: float64
diff_group = buy_trades.groupby('diff').agg({
'quantity': 'mean',
'diff': 'last',
})
diff_group['quantity'][diff_group['diff']>0][diff_group['diff']<0.01].plot(figsize=(10,5),grid=True);
Guncangan harga terjadi secara berkala
Hitung dampak harga dalam waktu 2 detik. Perbedaannya di sini adalah akan ada nilai negatif. Tentu saja, karena hanya order beli yang dihitung di sini, posisi simetris akan menjadi satu tick lebih besar. Terus amati hubungan antara volume perdagangan dan dampaknya, dan hitung hanya hasil yang lebih besar dari 0. Kesimpulannya mirip dengan kesimpulan dari satu order, yang juga merupakan hubungan linear perkiraan. Setiap tick membutuhkan sekitar 2000 volume.
df_resampled = buy_trades.resample('2S').agg({
'price': ['first', 'last', 'count'],
'quantity': 'sum'
})
df_resampled['price_diff'] = round(df_resampled[('price', 'last')] - df_resampled[('price', 'first')],3)
df_resampled['price_diff'] = df_resampled['price_diff'].fillna(0)
result_df_raw = pd.DataFrame({
'price_diff': df_resampled['price_diff'],
'quantity_sum': df_resampled[('quantity', 'sum')],
'data_count': df_resampled[('price', 'count')]
})
result_df = result_df_raw[result_df_raw['price_diff'] != 0]
result_df['price_diff'][abs(result_df['price_diff'])<0.016].value_counts().sort_index().plot.bar(figsize=(10,5));
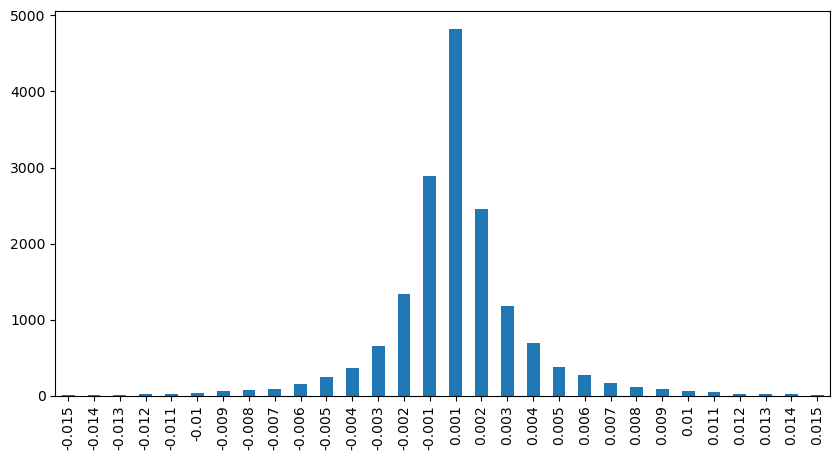
result_df['price_diff'].value_counts()[result_df['price_diff'].value_counts()>30]
0.001 7176
-0.001 3665
0.002 3069
-0.002 1536
0.003 1260
0.004 692
-0.003 608
0.005 391
-0.004 322
0.006 259
-0.005 192
0.007 146
-0.006 112
0.008 82
0.009 75
-0.007 75
-0.008 65
0.010 51
0.011 41
-0.010 31
Name: price_diff, dtype: int64
diff_group = result_df.groupby('price_diff').agg({ 'quantity_sum': 'mean'})
diff_group[(diff_group.index>0) & (diff_group.index<0.015)].plot(figsize=(10,5),grid=True);
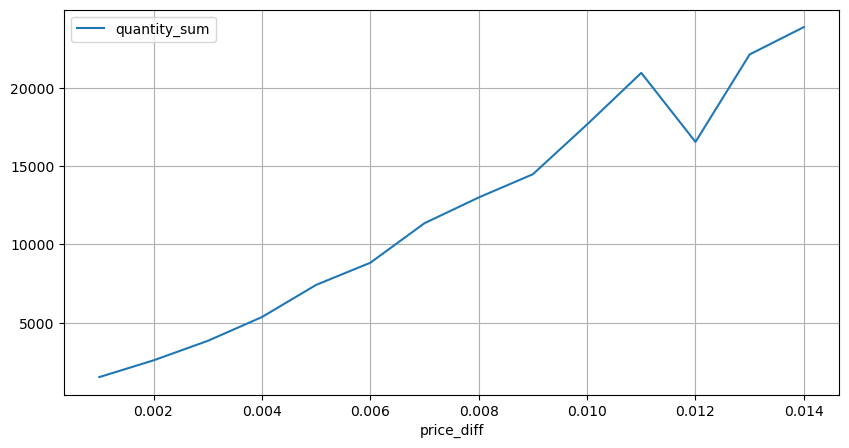
Dampak harga terhadap volume
Volume yang diperlukan untuk perubahan centang telah dihitung sebelumnya, tetapi tidak akurat karena didasarkan pada asumsi bahwa dampak telah terjadi. Sekarang mari kita lihat dampak harga yang disebabkan oleh volume perdagangan.
Data di sini diambil sampelnya pada 1 detik, dengan 100 kuantitas sebagai 1 langkah, dan perubahan harga dalam rentang kuantitas ini dihitung. Beberapa kesimpulan berharga telah ditarik:
- Bila volume beli di bawah 500, perubahan harga yang diharapkan turun, yang memang diharapkan karena ada juga perintah jual yang memengaruhi harga.
- Bila volume perdagangan rendah, maka mengikuti hubungan linear, yakni makin besar volume perdagangan, makin besar pula kenaikan harga.
- Semakin besar volume order beli, semakin besar pula perubahan harga, yang sering kali merupakan terobosan harga. Setelah terobosan tersebut, harga dapat kembali naik. Ditambah dengan pengambilan sampel pada interval tertentu, data menjadi tidak stabil.
- Perhatian harus diberikan pada bagian atas diagram sebar, yaitu bagian di mana volume sesuai dengan kenaikan harga.
- Untuk pasangan perdagangan ini saja, versi kasar hubungan antara volume dan perubahan harga diberikan:
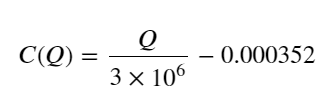
Di antara keduanya, “C” melambangkan perubahan harga dan “Q” melambangkan volume pesanan beli.
df_resampled = buy_trades.resample('1S').agg({
'price': ['first', 'last', 'count'],
'quantity': 'sum'
})
df_resampled['price_diff'] = round(df_resampled[('price', 'last')] - df_resampled[('price', 'first')],3)
df_resampled['price_diff'] = df_resampled['price_diff'].fillna(0)
result_df_raw = pd.DataFrame({
'price_diff': df_resampled['price_diff'],
'quantity_sum': df_resampled[('quantity', 'sum')],
'data_count': df_resampled[('price', 'count')]
})
result_df = result_df_raw[result_df_raw['price_diff'] != 0]
df = result_df.copy()
bins = np.arange(0, 30000, 100) #
labels = [f'{i}-{i+100-1}' for i in bins[:-1]]
df.loc[:, 'quantity_group'] = pd.cut(df['quantity_sum'], bins=bins, labels=labels)
grouped = df.groupby('quantity_group')['price_diff'].mean()
grouped_df = pd.DataFrame(grouped).reset_index()
grouped_df['quantity_group_center'] = grouped_df['quantity_group'].apply(lambda x: (float(x.split('-')[0]) + float(x.split('-')[1])) / 2)
plt.figure(figsize=(10,5))
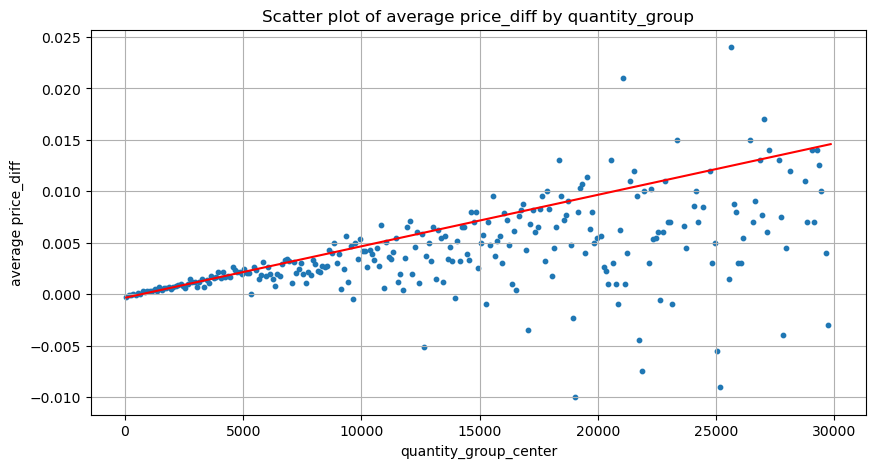
plt.scatter(grouped_df['quantity_group_center'], grouped_df['price_diff'],s=10)
plt.plot(grouped_df['quantity_group_center'], np.array(grouped_df['quantity_group_center'].values)/2e6-0.000352,color='red')
plt.xlabel('quantity_group_center')
plt.ylabel('average price_diff')
plt.title('Scatter plot of average price_diff by quantity_group')
plt.grid(True)
grouped_df.head(10)
| quantity_group | price_diff | quantity_group_center | |
|---|---|---|---|
| 0 | 0-199 | -0.000302 | 99.5 |
| 1 | 100-299 | -0.000124 | 199.5 |
| 2 | 200-399 | -0.000068 | 299.5 |
| 3 | 300-499 | -0.000017 | 399.5 |
| 4 | 400-599 | -0.000048 | 499.5 |
| 5 | 500-699 | 0.000098 | 599.5 |
| 6 | 600-799 | 0.000006 | 699.5 |
| 7 | 700-899 | 0.000261 | 799.5 |
| 8 | 800-999 | 0.000186 | 899.5 |
| 9 | 900-1099 | 0.000299 | 999.5 |
Posisi pesanan awal yang optimal
Dengan pemodelan volume perdagangan dan model kasar volume perdagangan yang sesuai dengan dampak harga, tampaknya posisi pesanan optimal dapat dihitung. Mari kita membuat beberapa asumsi dan memberikan posisi harga optimal yang tidak bertanggung jawab.
- Asumsikan bahwa harga kembali ke nilai aslinya setelah guncangan (ini tentu saja tidak mungkin dan memerlukan analisis ulang terhadap perubahan harga setelah guncangan)
- Asumsikan bahwa distribusi volume perdagangan dan frekuensi pesanan selama periode ini memenuhi persyaratan yang telah ditetapkan (ini juga tidak akurat, karena nilai satu hari digunakan untuk estimasi, dan transaksi memiliki pengelompokan yang jelas).
- Asumsikan hanya satu perintah jual yang terjadi selama waktu simulasi dan kemudian posisi ditutup.
- Dengan asumsi bahwa setelah order dieksekusi, ada order beli lain yang akan terus mendorong harga naik, terutama saat volume sangat rendah. Efek ini diabaikan di sini dan diasumsikan akan kembali.
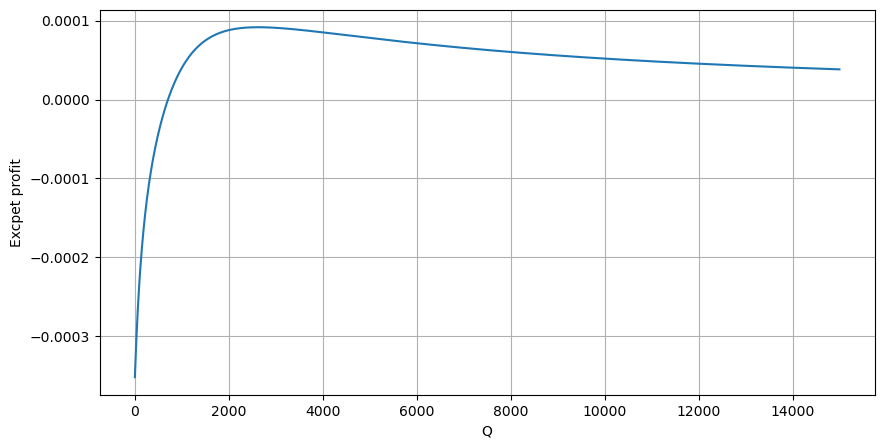
Pertama, tuliskan ekspektasi pengembalian sederhana, yaitu probabilitas bahwa pesanan beli kumulatif lebih besar dari Q dalam 1 detik, dikalikan dengan tingkat pengembalian yang diharapkan (yaitu, harga dampak):
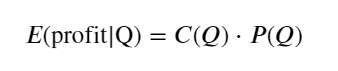
Berdasarkan grafik, laba yang diharapkan maksimum berada pada kisaran 2500, yaitu sekitar 2,5 kali volume perdagangan rata-rata. Dengan kata lain, perintah jual sebaiknya ditempatkan pada harga 2500. Perlu ditegaskan lagi bahwa sumbu horizontal mewakili volume perdagangan dalam 1 detik dan tidak bisa begitu saja disamakan dengan posisi kedalaman. Dan ini terjadi ketika masih kekurangan data mendalam yang sangat penting, dan hanya didasarkan pada spekulasi berdasarkan perdagangan.
Meringkaskan
Ditemukan bahwa distribusi volume pada interval waktu yang berbeda merupakan penskalaan sederhana dari distribusi volume satu transaksi. Kami juga membuat model pengembalian yang diharapkan sederhana berdasarkan guncangan harga dan probabilitas transaksi. Hasil model ini sesuai dengan harapan kami. Jika volume order jual kecil, itu menunjukkan penurunan harga. Jumlah tertentu diperlukan untuk mendapatkan keuntungan margin, dan semakin besar volume transaksi, semakin tinggi margin keuntungan. Semakin besar probabilitasnya, semakin rendah. Ada ukuran optimal di tengah, yang juga merupakan posisi penempatan order yang dicari oleh strategi. Tentu saja, model ini masih terlalu sederhana. Pada artikel berikutnya, saya akan terus membahasnya secara mendalam.
#1s内的累计分布
df_resampled = buy_trades['quantity'].resample('1S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 15000, 10))
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
profit_s = np.array([depth/2e6-0.000352 for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities_s*profit_s)
plt.xlabel('Q')
plt.ylabel('Excpet profit')
plt.grid(True)