Pemikiran tentang strategi perdagangan frekuensi tinggi (3)
 0
0
 2665
2665

Dalam artikel sebelumnya, saya memperkenalkan cara memodelkan volume perdagangan kumulatif dan menganalisis secara singkat fenomena guncangan harga. Artikel ini akan terus menganalisis data pesanan perdagangan. Dalam dua hari terakhir, YGG meluncurkan kontrak berbasis Binance U, dan harganya berfluktuasi sangat besar, dan volume perdagangan bahkan melampaui BTC pada satu titik. Mari kita analisis hari ini.
Interval waktu pemesanan
Secara umum, diasumsikan bahwa waktu kedatangan pesanan mengikuti proses Poisson. Berikut adalah artikel yang memperkenalkanProses Poisson . Saya akan menunjukkannya di bawah.
Unduh aggTrades pada tanggal 5 Agustus, totalnya ada 1.931.193 perdagangan, yang cukup dibesar-besarkan. Pertama, mari kita lihat distribusi order beli. Kita dapat melihat bahwa ada puncak lokal yang tidak merata di sekitar 100 ms dan 500 ms. Hal ini seharusnya disebabkan oleh order terjadwal yang ditempatkan oleh robot yang dipercayakan oleh Iceberg. Ini mungkin juga salah satu alasan mengapa kondisi pasar pada hari itu tidak biasa.
Fungsi massa probabilitas (PMF) dari distribusi Poisson diberikan oleh:
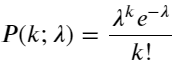
di dalam:
- k adalah jumlah kejadian yang kita minati.
- λ merupakan tingkat kemunculan rata-rata peristiwa per satuan waktu (atau satuan ruang).
- P(k; λ) merupakan probabilitas terjadinya tepat k peristiwa, dengan tingkat kejadian rata-rata λ.
Dalam proses Poisson, interval waktu antara kejadian mengikuti distribusi eksponensial. Fungsi kepadatan probabilitas (PDF) dari distribusi eksponensial diberikan oleh:
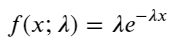
Melalui pencocokan, ditemukan bahwa hasil yang diperoleh cukup berbeda dari hasil yang diharapkan dari distribusi Poisson. Proses Poisson meremehkan frekuensi interval panjang dan melebih-lebihkan frekuensi interval pendek. (Distribusi interval sebenarnya lebih dekat dengan distribusi Pareto yang dimodifikasi)
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
trades = pd.read_csv('YGGUSDT-aggTrades-2023-08-05.csv')
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
buy_trades.index = buy_trades['date']
buy_trades['interval'][buy_trades['interval']<1000].plot.hist(bins=200,figsize=(10, 5));
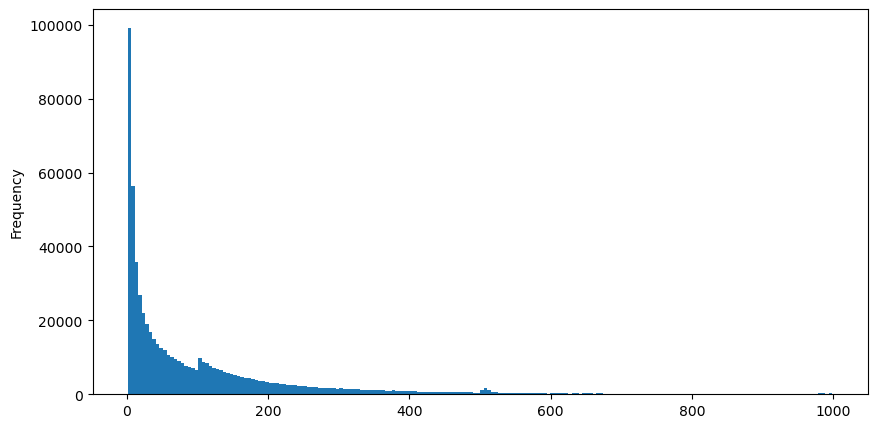
Intervals = np.array(range(0, 1000, 5))
mean_intervals = buy_trades['interval'].mean()
buy_rates = 1000/mean_intervals
probabilities = np.array([np.mean(buy_trades['interval'] > interval) for interval in Intervals])
probabilities_s = np.array([np.e**(-buy_rates*interval/1000) for interval in Intervals])
plt.figure(figsize=(10, 5))
plt.plot(Intervals, probabilities)
plt.plot(Intervals, probabilities_s)
plt.xlabel('Intervals')
plt.ylabel('Probability')
plt.grid(True)
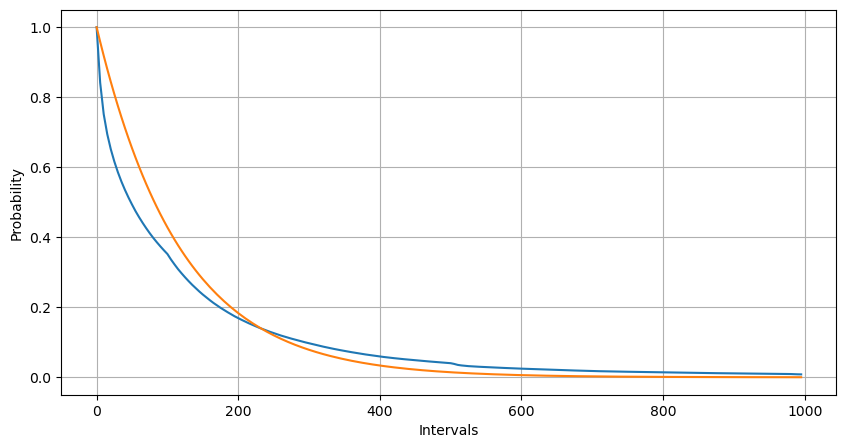
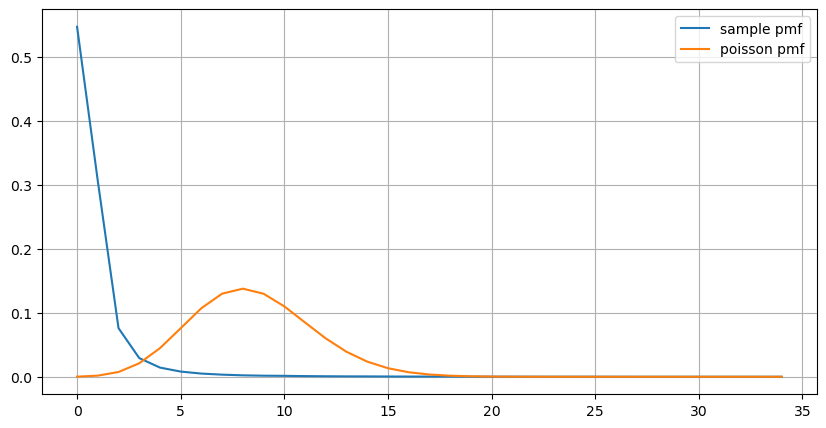
Distribusi statistik jumlah pesanan yang terjadi dalam 1 detik dan perbandingannya dengan distribusi Poisson juga menunjukkan perbedaan yang sangat jelas. Distribusi Poisson secara signifikan meremehkan frekuensi kejadian berprobabilitas rendah. Kemungkinan penyebabnya:
- Laju kejadian yang tidak konstan: Proses Poisson mengasumsikan bahwa laju rata-rata kejadian yang terjadi dalam periode waktu tertentu adalah konstan. Jika asumsi ini tidak berlaku, maka distribusi data akan menyimpang dari distribusi Poisson.
- Interaksi proses: Asumsi dasar lain dari proses Poisson adalah bahwa kejadian-kejadian tersebut bersifat independen satu sama lain. Jika kejadian di dunia nyata saling mempengaruhi, distribusinya mungkin menyimpang dari distribusi Poisson.
Dengan kata lain, dalam lingkungan nyata, frekuensi pesanan tidak konstan, perlu diperbarui secara real time, dan insentif akan terjadi, artinya, lebih banyak pesanan dalam waktu tertentu akan merangsang lebih banyak pesanan. Hal ini membuat mustahil untuk memperbaiki satu parameter pun dalam strategi.
result_df = buy_trades.resample('0.1S').agg({
'price': 'count',
'quantity': 'sum'
}).rename(columns={'price': 'order_count', 'quantity': 'quantity_sum'})
count_df = result_df['order_count'].value_counts().sort_index()[result_df['order_count'].value_counts()>20]
(count_df/count_df.sum()).plot(figsize=(10,5),grid=True,label='sample pmf');
from scipy.stats import poisson
prob_values = poisson.pmf(count_df.index, 1000/mean_intervals)
plt.plot(count_df.index, prob_values,label='poisson pmf');
plt.legend() ;
Parameter pembaruan waktu nyata
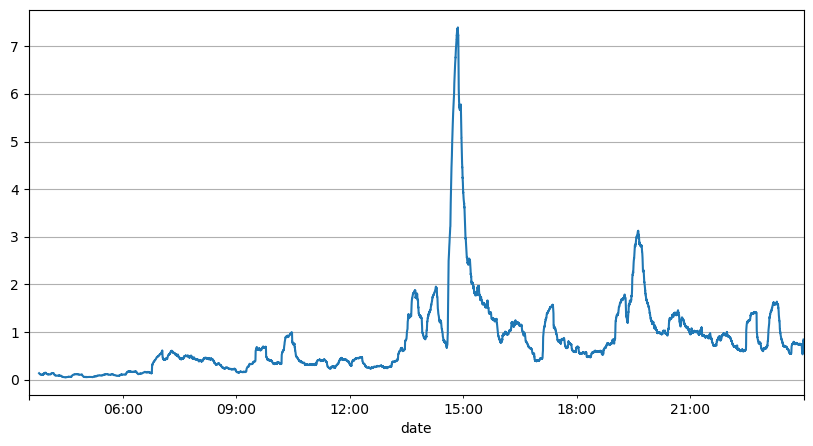
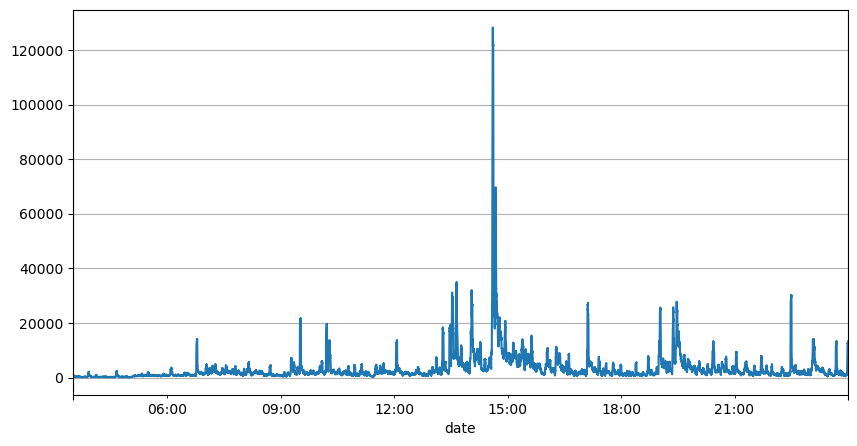
Analisis interval order sebelumnya menunjukkan bahwa parameter tetap tidak cocok untuk kondisi pasar riil, dan parameter utama deskripsi pasar strategi perlu diperbarui secara real time. Solusi yang paling mudah untuk dipikirkan adalah rata-rata pergerakan jendela geser. Dua gambar di bawah ini adalah frekuensi order beli dalam 1 detik dan rata-rata 1000 jendela volume perdagangan. Dapat dilihat bahwa ada fenomena pengelompokan dalam transaksi, yaitu frekuensi order secara signifikan lebih tinggi dari biasanya untuk periode waktu tertentu, dan volume pada saat ini juga meningkat secara serempak. Di sini, rata-rata sebelumnya digunakan untuk memprediksi nilai detik terakhir, dan kesalahan absolut rata-rata dari residual digunakan untuk mengukur kualitas prediksi.
Dari grafik tersebut, kita juga dapat memahami mengapa frekuensi orde sangat menyimpang dari distribusi Poisson. Meskipun jumlah rata-rata orde per detik hanya 8,5 kali, dalam kasus ekstrem jumlah rata-rata orde per detik menyimpang jauh darinya.
Di sini ditemukan bahwa penggunaan rata-rata dua detik sebelumnya untuk memprediksi kesalahan residual adalah yang terkecil dan jauh lebih baik daripada hasil prediksi rata-rata sederhana.
result_df['order_count'][::10].rolling(1000).mean().plot(figsize=(10,5),grid=True);
result_df
| order_count | quantity_sum | |
|---|---|---|
| 2023-08-05 03:30:06.100 | 1 | 76.0 |
| 2023-08-05 03:30:06.200 | 0 | 0.0 |
| 2023-08-05 03:30:06.300 | 0 | 0.0 |
| 2023-08-05 03:30:06.400 | 1 | 416.0 |
| 2023-08-05 03:30:06.500 | 0 | 0.0 |
| … | … | … |
| 2023-08-05 23:59:59.500 | 3 | 9238.0 |
| 2023-08-05 23:59:59.600 | 0 | 0.0 |
| 2023-08-05 23:59:59.700 | 1 | 3981.0 |
| 2023-08-05 23:59:59.800 | 0 | 0.0 |
| 2023-08-05 23:59:59.900 | 2 | 534.0 |
result_df['quantity_sum'].rolling(1000).mean().plot(figsize=(10,5),grid=True);
(result_df['order_count'] - result_df['mean_count'].mean()).abs().mean()
6.985628185332997
result_df['mean_count'] = result_df['order_count'].ewm(alpha=0.11, adjust=False).mean()
(result_df['order_count'] - result_df['mean_count'].shift()).abs().mean()
0.6727616961866929
result_df['mean_quantity'] = result_df['quantity_sum'].ewm(alpha=0.1, adjust=False).mean()
(result_df['quantity_sum'] - result_df['mean_quantity'].shift()).abs().mean()
4180.171479076811
Meringkaskan
Artikel ini secara singkat memperkenalkan alasan mengapa interval waktu orde menyimpang dari proses Poisson, terutama karena parameternya berubah seiring waktu. Untuk memprediksi pasar secara lebih akurat, strategi perlu membuat prediksi waktu nyata mengenai parameter dasar pasar. Residual dapat digunakan untuk mengukur kualitas prediksi. Contoh di atas adalah yang paling sederhana. Ada banyak penelitian terkait tentang analisis deret waktu, agregasi volatilitas, dll., yang dapat ditingkatkan lebih lanjut.