Artikel sebelumnya mempelajari interval kedatangan pesanan dan menunjukkan mengapa kita perlu menyesuaikan parameter secara dinamis dan cara mengevaluasi kualitas estimasi. Artikel ini akan berfokus pada data mendalam dan mempelajari harga tengah (juga disebut harga wajar, harga mikro, dll.).

Data Kedalaman

Binance menyediakan data historis yang dapat diunduh dari kutipan terbaik, termasuk best_bid_price: harga penawaran terbaik, yaitu harga penawaran maksimum, best_bid_qty: jumlah harga penawaran terbaik, best_ask_price: harga permintaan terbaik, best_ask_qty: jumlah harga permintaan terbaik , transaction_time: stempel waktu. Data ini tidak mencakup pending order tingkat kedua dan yang lebih dalam. Situasi pasar yang dianalisis di sini adalah YGG pada 7 Agustus. Fluktuasi pasar pada hari itu sangat drastis, dan jumlah data mencapai lebih dari 9 juta.

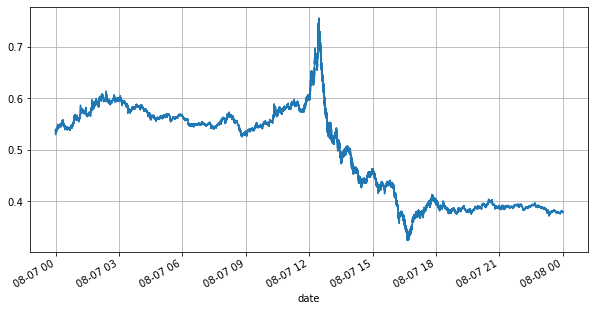
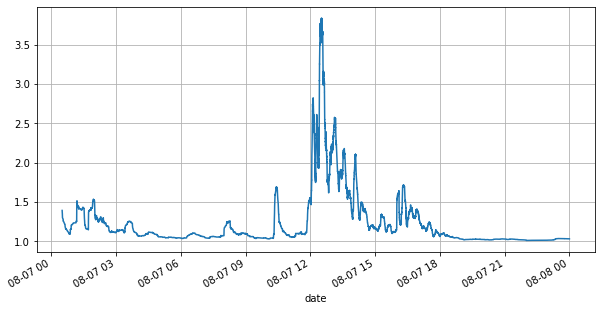
Pertama, mari kita lihat pasar hari ini. Pasar mengalami pasang surut yang hebat. Selain itu, jumlah pending order pada hari itu juga berubah drastis seiring dengan fluktuasi pasar. Secara khusus, spread (selisih antara harga jual dan harga beli) secara signifikan menunjukkan situasi Fluktuasi pasar. Menurut statistik pasar YGG pada hari itu, 20% dari waktu spread lebih besar dari 1 tick. Di era ketika berbagai robot bersaing di pasar, situasi ini jarang terjadi.

from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

books = pd.read_csv('YGGUSDT-bookTicker-2023-08-07.csv')

tick_size = 0.0001

books['date'] = pd.to_datetime(books['transaction_time'], unit='ms')
books.index = books['date']

books['spread'] = round(books['best_ask_price'] - books['best_bid_price'],4)

books['best_bid_price'][::10].plot(figsize=(10,5),grid=True);

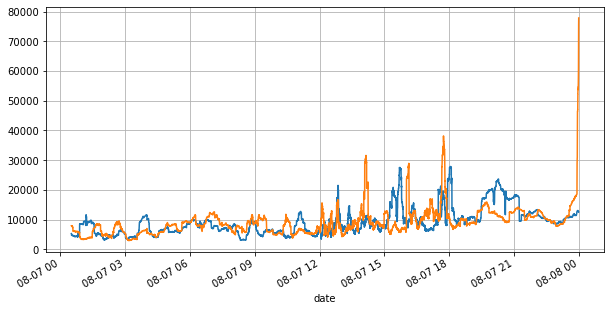
books['best_bid_qty'][::10].rolling(10000).mean().plot(figsize=(10,5),grid=True);
books['best_ask_qty'][::10].rolling(10000).mean().plot(figsize=(10,5),grid=True);

(books['spread'][::10]/tick_size).rolling(10000).mean().plot(figsize=(10,5),grid=True);

books['spread'].value_counts()[books['spread'].value_counts()>500]/books['spread'].value_counts().sum()

0.0001    0.799169
0.0002    0.102750
0.0003    0.042472
0.0004    0.022821
0.0005    0.012792
0.0006    0.007350
0.0007    0.004376
0.0008    0.002712
0.0009    0.001657
0.0010    0.001089
0.0011    0.000740
0.0012    0.000496
0.0013    0.000380
0.0014    0.000258
0.0015    0.000197
0.0016    0.000140
0.0017    0.000112
0.0018    0.000088
0.0019    0.000063
Name: spread, dtype: float64

Kutipan Tidak Seimbang

Dari uraian di atas, kita dapat melihat bahwa volume pesanan beli dan jual sangat berbeda pada sebagian besar waktu. Perbedaan ini memiliki efek prediktif yang kuat pada kondisi pasar jangka pendek. Alasannya mirip dengan alasan yang disebutkan dalam artikel sebelumnya bahwa pesanan beli kecil sering kali menyebabkan penurunan. Jika pending order di satu sisi jauh lebih kecil dibandingkan pending order di sisi lainnya, dan dengan asumsi bahwa volume order beli dan jual aktif hampir sama, sisi dengan pending order yang lebih kecil akan lebih mungkin dikonsumsi, sehingga mendorong kenaikan harga. perubahan. Kutipan yang tidak seimbang diwakili oleh I: 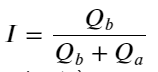Dimana Q_b melambangkan jumlah pesanan beli (best_bid_qty), dan Q_a melambangkan jumlah pesanan jual (best_ask_qty).

Tentukan harga tengah: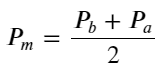

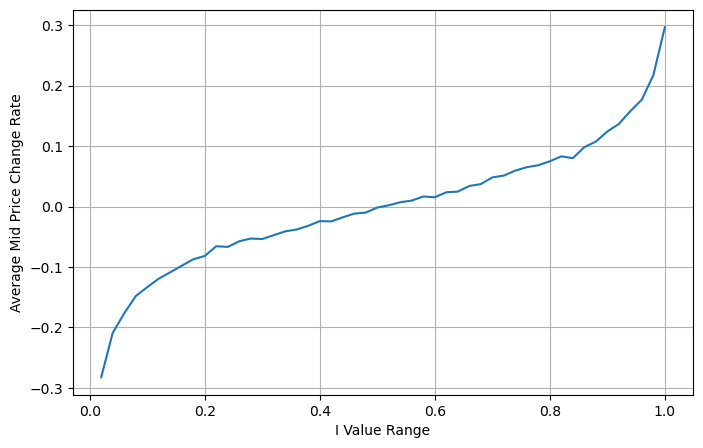
Gambar berikut menunjukkan hubungan antara tingkat perubahan harga tengah pada interval berikutnya dan ketidakseimbangan I. Seperti yang diharapkan, ketika I meningkat, harga cenderung naik dan semakin dekat ke 1, besarnya ketidakseimbangan I akan semakin besar. perubahan harga juga semakin cepat. Dalam perdagangan frekuensi tinggi, tujuan pengenalan harga tengah adalah untuk memprediksi perubahan harga di masa mendatang dengan lebih baik. Dengan kata lain, semakin kecil selisihnya dari harga di masa mendatang, semakin baik harga tengah didefinisikan. Jelas, ketidakseimbangan pending order memberikan informasi tambahan untuk prediksi strategi. Dengan mempertimbangkan hal ini, kami mendefinisikan harga tengah tertimbang:

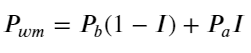
books['I'] = books['best_bid_qty'] / (books['best_bid_qty'] + books['best_ask_qty'])

books['mid_price'] = (books['best_ask_price'] + books['best_bid_price'])/2

bins = np.linspace(0, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['price_change'] = (books['mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['price_change'].mean()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Average Mid Price Change Rate');
plt.grid(True)

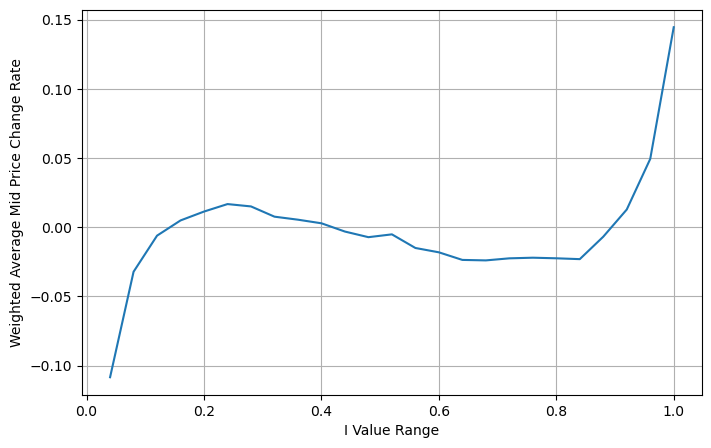
books['weighted_mid_price'] = books['mid_price'] + books['spread']*books['I']/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['weighted_price_change'] = (books['weighted_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['weighted_price_change'].mean()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

Sesuaikan harga tengah tertimbang

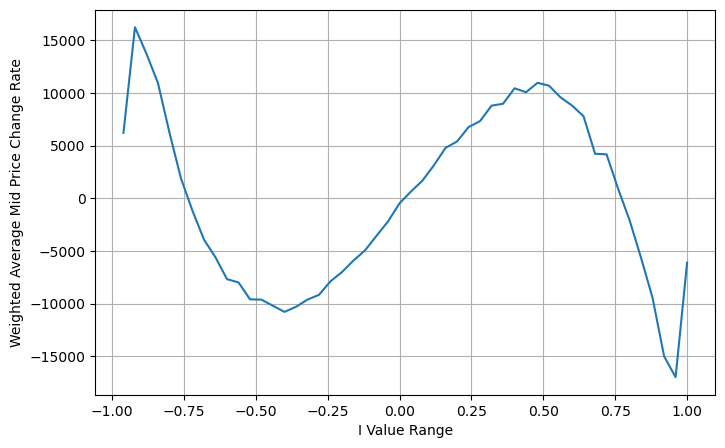
Dari gambar tersebut, kita dapat melihat bahwa harga tengah tertimbang berubah jauh lebih sedikit dibandingkan I yang berbeda, yang berarti bahwa harga tengah tertimbang lebih cocok. Namun masih ada beberapa keteraturan, seperti sekitar 0,2 dan 0,8, yang penyimpangannya relatif besar. Ini menunjukkan bahwa saya masih dapat memberikan informasi tambahan. Karena harga tengah tertimbang mengasumsikan bahwa suku koreksi harga sepenuhnya linier dengan I, hal ini jelas tidak benar. Seperti yang dapat dilihat dari gambar di atas, ketika I mendekati 0 dan 1, deviasinya lebih cepat dan bukan merupakan hubungan linier.

Untuk tampilan yang lebih intuitif, I didefinisikan ulang di sini:

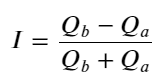
pada saat ini:

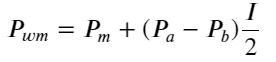
Dengan memperhatikan bentuk ini, kita dapat menemukan bahwa harga tengah tertimbang merupakan koreksi terhadap harga tengah rata-rata. Koefisien suku koreksi adalah Spread, dan suku koreksi merupakan fungsi dari I. Harga tengah tertimbang hanya mengasumsikan bahwa hubungan ini adalah I/2 Pada saat ini, keuntungan dari distribusi I (-1,1) yang disesuaikan tercermin. I simetris terhadap titik asal, yang memudahkan kita untuk menemukan hubungan fungsi yang sesuai. Perhatikan grafiknya, fungsi ini harus memenuhi hubungan pangkat ganjil I, yang konsisten dengan pertumbuhan cepat di kedua sisi dan simetri terhadap titik asal. Selain itu, dapat diamati bahwa nilai di dekat titik asal mendekati linier, dan ketika I bernilai 0, fungsi hasilnya adalah 0, dan ketika I bernilai 1, fungsi hasilnya adalah 0,5. Jadi kira-kira fungsinya seperti ini:

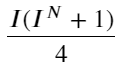
Di sini N adalah angka genap positif. Setelah pengujian aktual, lebih baik jika N adalah 8. Sejauh ini, artikel ini mengusulkan harga tengah tertimbang yang direvisi:

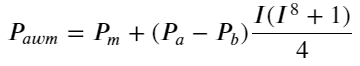
Pada titik ini, perubahan harga tengah yang diprediksi pada dasarnya tidak ada hubungannya dengan I. Meskipun hasil ini lebih baik daripada harga tengah tertimbang sederhana, namun tidak dapat diterapkan dalam perdagangan yang sebenarnya. Itu hanya sekadar ide yang diberikan di sini. Sebuah artikel tahun 2017 oleh S Stoikov memperkenalkan metode rantai MarkovMicro-Price, dan memberikan kode yang relevan, Anda juga dapat mempelajarinya.

books['I'] = (books['best_bid_qty'] - books['best_ask_qty']) / (books['best_bid_qty'] + books['best_ask_qty'])

books['weighted_mid_price'] = books['mid_price'] + books['spread']*books['I']/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['weighted_price_change'] = (books['weighted_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['weighted_price_change'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

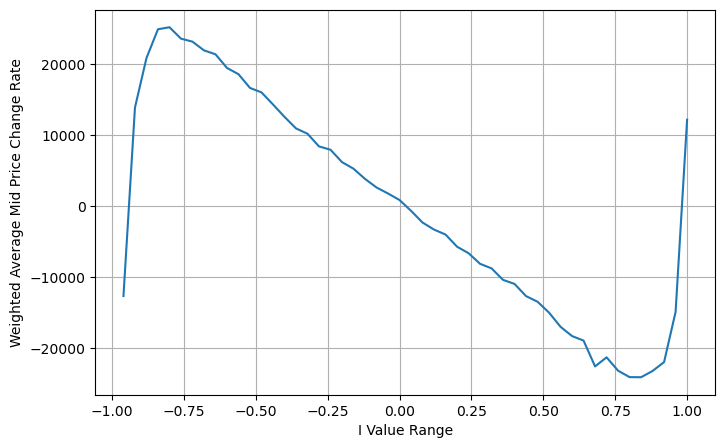
books['adjust_mid_price'] = books['mid_price'] + books['spread']*(books['I'])*(books['I']**8+1)/4
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['adjust_mid_price'] = (books['adjust_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['adjust_mid_price'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

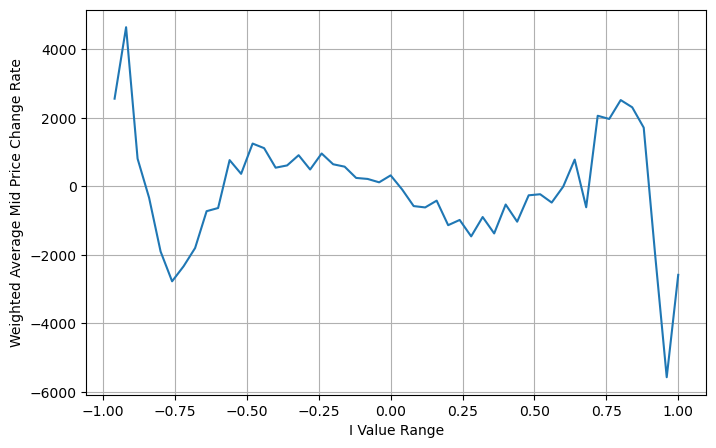
books['adjust_mid_price'] = books['mid_price'] + books['spread']*(books['I']**3)/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['adjust_mid_price'] = (books['adjust_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['adjust_mid_price'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

Meringkaskan

Harga tengah sangat penting untuk strategi frekuensi tinggi. Harga tengah merupakan prediksi harga jangka pendek di masa mendatang, jadi harga tengah harus seakurat mungkin. Harga tengah yang diperkenalkan di atas semuanya berdasarkan data pasar, karena hanya satu harga pasar yang digunakan dalam analisis. Dalam perdagangan nyata, strategi harus menggunakan semua data sebanyak mungkin, terutama ketika ada pertukaran perdagangan dalam perdagangan nyata, dan prediksi harga tengah harus diuji dengan harga transaksi aktual. Saya ingat Stoikov tampaknya telah memposting sebuah tweet yang mengatakan bahwa harga tengah yang sebenarnya seharusnya adalah rata-rata tertimbang dari probabilitas transaksi beli-satu-jual. Masalah ini baru saja dipelajari dalam artikel sebelumnya. Karena keterbatasan ruang, masalah ini akan dibahas secara rinci dalam artikel berikutnya.