Dalam artikel ini, kami akan menulis strategi perdagangan harian. Ini akan menggunakan konsep perdagangan klasik “pasangan perdagangan mean reversion”. Dalam contoh ini, kami akan menggunakan dua dana yang diperdagangkan di bursa (ETF), SPY dan IWM, yang diperdagangkan di Bursa Efek New York (NYSE) dan mencoba mewakili indeks pasar saham AS, S&P 500 dan Russell 2000. .

Strategi ini menciptakan “carry” dengan mengambil posisi long pada satu ETF dan short pada ETF lainnya. Rasio panjang-pendek dapat didefinisikan dalam banyak cara, misalnya menggunakan metode deret waktu kointegrasi statistik. Dalam skenario ini, kami akan menghitung rasio lindung nilai antara SPY dan IWM melalui regresi linier bergulir. Hal ini akan memungkinkan kita untuk membuat “spread” antara SPY dan IWM yang dinormalisasi ke skor-z. Ketika skor-z melampaui ambang batas tertentu, sinyal perdagangan dihasilkan karena kami yakin bahwa “spread” ini akan kembali ke rata-rata.

Alasan di balik strategi ini adalah bahwa SPY dan IWM mewakili skenario pasar yang hampir sama, yaitu kinerja harga saham sekelompok perusahaan besar dan kecil AS. Asumsinya adalah jika Anda menerima teori harga “mean reversion”, maka teori tersebut akan selalu kembali, karena “peristiwa” dapat memengaruhi S&P500 dan Russell 2000 secara terpisah dalam waktu yang sangat singkat, tetapi “perbedaan suku bunga” antara mereka akan selalu kembali ke rata-rata normal, dan rangkaian harga jangka panjang keduanya selalu terkointegrasi.

Strategi

Strategi ini dilaksanakan sebagai berikut:

Data - Dapatkan grafik lilin 1 menit SPY dan IWM dari April 2007 hingga Februari 2014.

Pemrosesan - Sejajarkan data dengan benar dan hapus batangan yang hilang satu sama lain. (Jika salah satu sisi hilang, kedua sisi akan dihapus)

Spread - Rasio lindung nilai antara dua ETF dihitung menggunakan regresi linier bergulir. Didefinisikan sebagai koefisien regresi beta menggunakan jendela lihat balik yang digeser maju sejauh 1 batang dan koefisien regresi dihitung ulang. Oleh karena itu, rasio lindung nilai βi, bi K-line digunakan untuk menelusuri garis K dengan menghitung titik perpotongan dari bi-1-k ke bi-1.

Z-Score - Nilai Spread Standar dihitung dengan cara biasa. Ini berarti mengurangi rata-rata penyebaran (sampel) dan membaginya dengan deviasi standar penyebaran (sampel). Alasan melakukan ini adalah untuk membuat parameter ambang batas lebih mudah dipahami karena Z-Score merupakan besaran tak berdimensi. Saya sengaja memasukkan “bias lookahead” ke dalam perhitungan untuk menunjukkan betapa halusnya hal itu. Cobalah!

Perdagangan - Sinyal panjang dihasilkan ketika nilai z-skor negatif turun di bawah ambang batas yang telah ditentukan sebelumnya (atau pasca-optimal), sementara sinyal pendek dihasilkan sebaliknya. Ketika nilai absolut skor-z turun di bawah ambang batas tambahan, sinyal untuk menutup posisi dihasilkan. Untuk strategi ini, saya (agak sewenang-wenang) memilih |z| = 2 sebagai ambang batas masuk dan |z| = 1 sebagai ambang batas keluar. Dengan asumsi mean reversion memainkan peranan dalam spread, uraian di atas diharapkan dapat menangkap hubungan arbitrase ini dan memberikan keuntungan besar.

Mungkin cara terbaik untuk memahami suatu strategi secara mendalam adalah dengan benar-benar menerapkannya. Bagian berikut merinci kode Python lengkap (file tunggal) yang digunakan untuk menerapkan strategi pembalikan rata-rata ini. Saya telah menambahkan komentar kode terperinci untuk membantu Anda memahami lebih baik.

Implementasi Python

Seperti semua tutorial Python/pandas, lingkungan Python Anda harus disiapkan seperti yang dijelaskan dalam tutorial ini. Setelah pengaturan selesai, tugas pertama adalah mengimpor pustaka Python yang diperlukan. Ini diperlukan untuk menggunakan matplotlib dan pandas.

Versi pustaka spesifik yang saya gunakan adalah sebagai berikut:

Python - 2.7.3 NumPy - 1.8.0 pandas - 0.12.0 matplotlib - 1.1.0

Mari kita lanjutkan dan impor pustaka ini:

# mr_spy_iwm.py

import matplotlib.pyplot as plt
import numpy as np
import os, os.path
import pandas as pd

Fungsi create_pairs_dataframe berikut mengimpor dua file CSV yang berisi kandil intraday dari dua simbol. Dalam kasus kami, ini adalah SPY dan IWM. Kemudian menciptakan “sepasang bingkai data” terpisah yang menggunakan indeks kedua file asli. Stempel waktunya dapat bervariasi karena adanya transaksi yang terlewat dan kesalahan. Ini adalah salah satu manfaat utama menggunakan pustaka analisis data seperti pandas. Kami menangani kode “boilerplate” dengan cara yang sangat efisien.

# mr_spy_iwm.py
def create_pairs_dataframe(datadir, symbols):
    """Creates a pandas DataFrame containing the closing price
    of a pair of symbols based on CSV files containing a datetime
    stamp and OHLCV data."""
 
    # Open the individual CSV files and read into pandas DataFrames
    print "Importing CSV data..."
    sym1 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[0]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
    sym2 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[1]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
 
    # Create a pandas DataFrame with the close prices of each symbol
    # correctly aligned and dropping missing entries
    print "Constructing dual matrix for %s and %s..." % symbols    
    pairs = pd.DataFrame(index=sym1.index)
    pairs['%s_close' % symbols[0].lower()] = sym1['close']
    pairs['%s_close' % symbols[1].lower()] = sym2['close']
    pairs = pairs.dropna()
    return pairs

Langkah berikutnya adalah melakukan regresi linier bergulir antara SPY dan IWM. Dalam skenario ini, IWM adalah prediktor (‘x’) dan SPY adalah respons (‘y’). Saya menetapkan jendela lihat balik default sejumlah 100 kandil. Seperti disebutkan di atas, ini adalah parameter strategi. Agar suatu strategi dianggap tangguh, idealnya kita ingin melihat laporan pengembalian yang cembung selama periode tinjauan balik (atau beberapa ukuran kinerja lainnya). Oleh karena itu, pada tahap kode selanjutnya, kami akan melakukan analisis sensitivitas dengan memvariasikan periode tinjauan balik dalam cakupannya.

Setelah menghitung koefisien beta bergulir dalam model regresi linier untuk SPY-IWM, tambahkan ke pasangan DataFrame dan hapus baris kosong. Ini membangun rangkaian kandil pertama, yang sama dengan ukuran pemangkasan panjang tinjauan balik. Kami kemudian membuat selisih antara dua ETF, satu unit SPY dan satu unit -βi IWM. Jelas ini bukan skenario yang realistis, karena kami menggunakan IWM dalam jumlah kecil, yang tidak mungkin dilakukan dalam implementasi praktis.

Terakhir, kami membuat skor-z dari spread, dihitung dengan cara mengurangi rata-rata spread dan menormalkannya dengan deviasi standar spread. Penting untuk dicatat bahwa ada “bias berwawasan ke depan” yang agak halus dalam hal ini. Saya sengaja membiarkannya dalam kode karena saya ingin menyoroti betapa mudahnya membuat kesalahan seperti ini dalam penelitian. Hitunglah nilai rata-rata dan deviasi standar dari seluruh rangkaian waktu sebaran. Jika ini dimaksudkan untuk mencerminkan akurasi sejarah yang sebenarnya, maka informasi ini tidak dapat diperoleh karena secara implisit memanfaatkan informasi dari masa depan. Oleh karena itu, kita harus menggunakan rata-rata bergulir dan stdev untuk menghitung skor-z.

# mr_spy_iwm.py
 
def calculate_spread_zscore(pairs, symbols, lookback=100):
    """Creates a hedge ratio between the two symbols by calculating
    a rolling linear regression with a defined lookback period. This
    is then used to create a z-score of the 'spread' between the two
    symbols based on a linear combination of the two."""
     
    # Use the pandas Ordinary Least Squares method to fit a rolling
    # linear regression between the two closing price time series
    print "Fitting the rolling Linear Regression..."
    model = pd.ols(y=pairs['%s_close' % symbols[0].lower()], 
                   x=pairs['%s_close' % symbols[1].lower()],
                   window=lookback)
 
    # Construct the hedge ratio and eliminate the first 
    # lookback-length empty/NaN period
    pairs['hedge_ratio'] = model.beta['x']
    pairs = pairs.dropna()
 
    # Create the spread and then a z-score of the spread
    print "Creating the spread/zscore columns..."
    pairs['spread'] = pairs['spy_close'] - pairs['hedge_ratio']*pairs['iwm_close']
    pairs['zscore'] = (pairs['spread'] - np.mean(pairs['spread']))/np.std(pairs['spread'])
    return pairs

Dalam create_long_short_market_signals, buat sinyal perdagangan. Angka ini dihitung dengan mengukur nilai z-skor yang melampaui ambang batas. Bila nilai absolut skor-z kurang dari atau sama dengan ambang batas lain (yang lebih kecil), sinyal untuk menutup posisi diberikan.

Untuk mencapai hal ini, perlu ditetapkan apakah strategi perdagangannya adalah “pembukaan” atau “penutupan” untuk setiap garis K. Long_market dan short_market adalah dua variabel yang ditetapkan untuk melacak posisi panjang dan pendek. Sayangnya, komputasinya lambat karena jauh lebih mudah diprogram secara berulang daripada pendekatan vektor. Meskipun grafik candlestick 1 menit memerlukan ~700.000 titik data per file CSV, perhitungannya masih relatif cepat di desktop lama saya!

Untuk mengulang pandas DataFrame (operasi yang memang tidak umum), perlu menggunakan metode iterrows, yang menyediakan generator yang dapat diulang:

# mr_spy_iwm.py
 
def create_long_short_market_signals(pairs, symbols, 
                                     z_entry_threshold=2.0, 
                                     z_exit_threshold=1.0):
    """Create the entry/exit signals based on the exceeding of 
    z_enter_threshold for entering a position and falling below
    z_exit_threshold for exiting a position."""
 
    # Calculate when to be long, short and when to exit
    pairs['longs'] = (pairs['zscore'] <= -z_entry_threshold)*1.0
    pairs['shorts'] = (pairs['zscore'] >= z_entry_threshold)*1.0
    pairs['exits'] = (np.abs(pairs['zscore']) <= z_exit_threshold)*1.0
 
    # These signals are needed because we need to propagate a
    # position forward, i.e. we need to stay long if the zscore
    # threshold is less than z_entry_threshold by still greater
    # than z_exit_threshold, and vice versa for shorts.
    pairs['long_market'] = 0.0
    pairs['short_market'] = 0.0
 
    # These variables track whether to be long or short while
    # iterating through the bars
    long_market = 0
    short_market = 0
 
    # Calculates when to actually be "in" the market, i.e. to have a
    # long or short position, as well as when not to be.
    # Since this is using iterrows to loop over a dataframe, it will
    # be significantly less efficient than a vectorised operation,
    # i.e. slow!
    print "Calculating when to be in the market (long and short)..."
    for i, b in enumerate(pairs.iterrows()):
        # Calculate longs
        if b[1]['longs'] == 1.0:
            long_market = 1            
        # Calculate shorts
        if b[1]['shorts'] == 1.0:
            short_market = 1
        # Calculate exists
        if b[1]['exits'] == 1.0:
            long_market = 0
            short_market = 0
        # This directly assigns a 1 or 0 to the long_market/short_market
        # columns, such that the strategy knows when to actually stay in!
        pairs.ix[i]['long_market'] = long_market
        pairs.ix[i]['short_market'] = short_market
    return pairs

Pada tahap ini, kami memperbarui pasangan untuk memuat sinyal panjang dan pendek aktual, yang memungkinkan kami menentukan apakah kami perlu membuka posisi. Sekarang kita perlu membuat portofolio untuk melacak nilai pasar dari posisi. Tugas pertama adalah membuat kolom posisi yang menggabungkan sinyal panjang dan pendek. Ini akan berisi daftar elemen dari (1,0,-1) di mana 1 mewakili posisi panjang, 0 mewakili tidak ada posisi (yang harus ditutup), dan -1 mewakili posisi pendek. Kolom sym1 dan sym2 mewakili nilai pasar posisi SPY dan IWM di akhir setiap kandil.

Setelah nilai pasar ETF dibuat, kami menjumlahkannya untuk menghasilkan nilai pasar total pada akhir setiap kandil. Kemudian diubah menjadi nilai balik melalui metode pct_change objek tersebut. Baris kode berikutnya membersihkan entri yang salah (elemen NaN dan inf) dan akhirnya menghitung kurva ekuitas lengkap.

# mr_spy_iwm.py
 
def create_portfolio_returns(pairs, symbols):
    """Creates a portfolio pandas DataFrame which keeps track of
    the account equity and ultimately generates an equity curve.
    This can be used to generate drawdown and risk/reward ratios."""
     
    # Convenience variables for symbols
    sym1 = symbols[0].lower()
    sym2 = symbols[1].lower()
 
    # Construct the portfolio object with positions information
    # Note that minuses to keep track of shorts!
    print "Constructing a portfolio..."
    portfolio = pd.DataFrame(index=pairs.index)
    portfolio['positions'] = pairs['long_market'] - pairs['short_market']
    portfolio[sym1] = -1.0 * pairs['%s_close' % sym1] * portfolio['positions']
    portfolio[sym2] = pairs['%s_close' % sym2] * portfolio['positions']
    portfolio['total'] = portfolio[sym1] + portfolio[sym2]
 
    # Construct a percentage returns stream and eliminate all 
    # of the NaN and -inf/+inf cells
    print "Constructing the equity curve..."
    portfolio['returns'] = portfolio['total'].pct_change()
    portfolio['returns'].fillna(0.0, inplace=True)
    portfolio['returns'].replace([np.inf, -np.inf], 0.0, inplace=True)
    portfolio['returns'].replace(-1.0, 0.0, inplace=True)
 
    # Calculate the full equity curve
    portfolio['returns'] = (portfolio['returns'] + 1.0).cumprod()
    return portfolio

Fungsi utama menyatukan semuanya. File CSV intraday terletak di jalur datadir. Pastikan Anda mengubah kode berikut untuk menunjuk ke direktori spesifik Anda.

Untuk menentukan seberapa sensitif strategi terhadap periode tinjauan balik, perlu dihitung serangkaian metrik kinerja tinjauan balik. Saya memilih persentase total pengembalian akhir portofolio sebagai metrik kinerja dan rentang tinjauan.[[50.200] dengan kenaikan 10. Anda dapat melihat pada kode di bawah ini bahwa fungsi sebelumnya dibungkus dalam for loop pada rentang ini dan ambang batas lainnya tetap sama. Tugas terakhir adalah membuat diagram garis lookback versus return menggunakan matplotlib:

# mr_spy_iwm.py
 
if __name__ == "__main__":
    datadir = '/your/path/to/data/'  # Change this to reflect your data path!
    symbols = ('SPY', 'IWM')
 
    lookbacks = range(50, 210, 10)
    returns = []
 
    # Adjust lookback period from 50 to 200 in increments
    # of 10 in order to produce sensitivities
    for lb in lookbacks: 
        print "Calculating lookback=%s..." % lb
        pairs = create_pairs_dataframe(datadir, symbols)
        pairs = calculate_spread_zscore(pairs, symbols, lookback=lb)
        pairs = create_long_short_market_signals(pairs, symbols, 
                                                z_entry_threshold=2.0, 
                                                z_exit_threshold=1.0)
 
        portfolio = create_portfolio_returns(pairs, symbols)
        returns.append(portfolio.ix[-1]['returns'])
 
    print "Plot the lookback-performance scatterchart..."
    plt.plot(lookbacks, returns, '-o')
    plt.show()

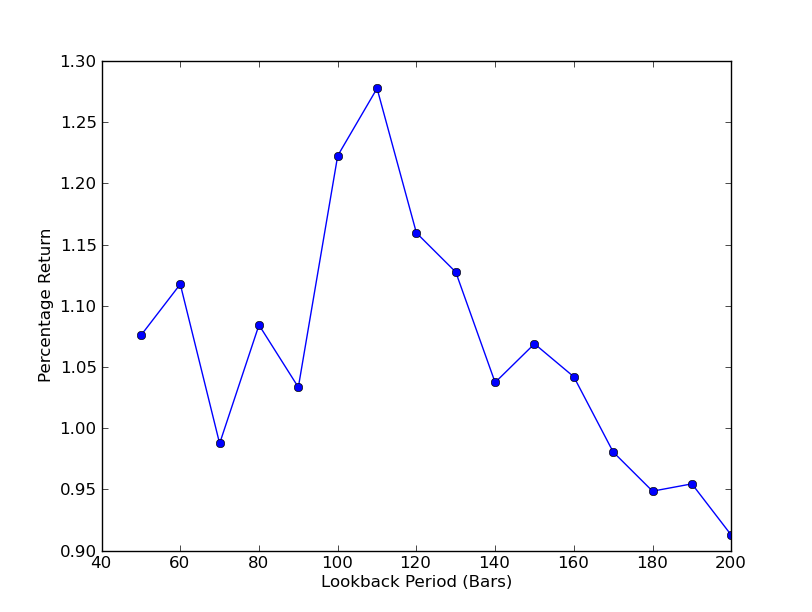
Sekarang Anda dapat melihat grafik tinjauan balik dan pengembalian. Perlu diperhatikan bahwa ada maksimum “global” untuk lookback, yang setara dengan 110 bar. Jika kita melihat situasi di mana lookback tidak ada hubungannya dengan pengembalian, itu karena:

Analisis Sensitivitas Rasio Lindung Nilai Regresi Linier SPY-IWM Periode Peninjauan Kembali

Artikel pengujian ulang mana pun tidak akan lengkap tanpa kurva keuntungan yang meningkat! Jadi jika Anda ingin memetakan laba kumulatif terhadap waktu, Anda dapat menggunakan kode berikut. Ini akan memetakan portofolio akhir yang dihasilkan dari studi parameter lookback. Oleh karena itu, perlu untuk memilih lookback sesuai dengan grafik yang ingin Anda visualisasikan. Grafik ini juga memetakan laba SPY selama periode yang sama untuk membantu perbandingan:

# mr_spy_iwm.py
 
    # This is still within the main function
    print "Plotting the performance charts..."
    fig = plt.figure()
    fig.patch.set_facecolor('white')
 
    ax1 = fig.add_subplot(211,  ylabel='%s growth (%%)' % symbols[0])
    (pairs['%s_close' % symbols[0].lower()].pct_change()+1.0).cumprod().plot(ax=ax1, color='r', lw=2.)
 
    ax2 = fig.add_subplot(212, ylabel='Portfolio value growth (%%)')
    portfolio['returns'].plot(ax=ax2, lw=2.)
 
    fig.show()

Grafik kurva ekuitas di bawah ini memiliki periode tinjauan kembali 100 hari:

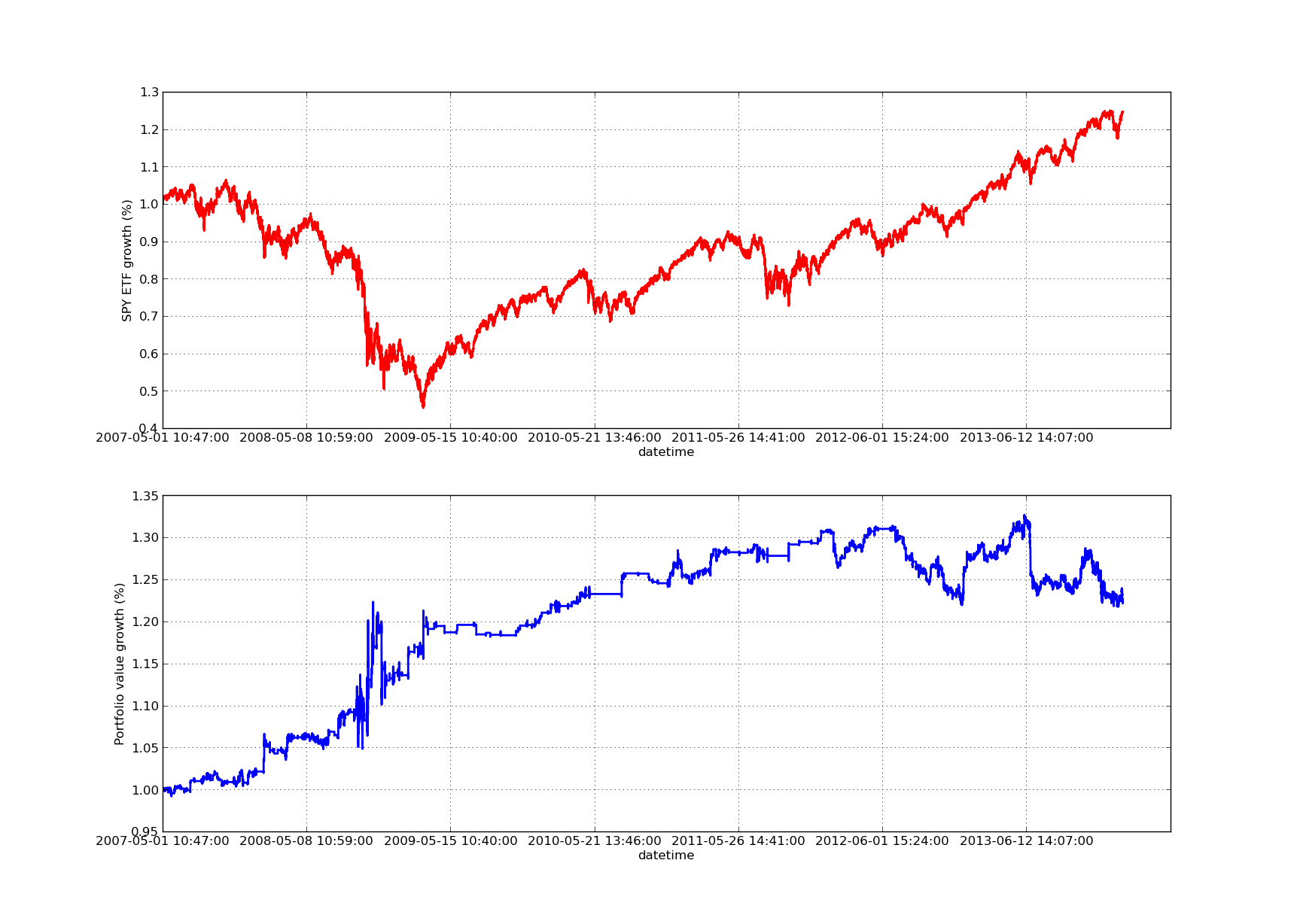
Analisis Sensitivitas Rasio Lindung Nilai Regresi Linier SPY-IWM Periode Peninjauan Kembali

Perhatikan bahwa penarikan SPY cukup besar pada tahun 2009 selama krisis keuangan. Strategi ini juga berada dalam masa yang penuh gejolak selama fase ini. Perhatikan pula bahwa kinerja telah memburuk selama setahun terakhir karena sifat tren SPY yang kuat selama periode ini yang mencerminkan S&P 500.

Perlu dicatat bahwa kita masih perlu memperhitungkan “bias lookahead” ketika menghitung sebaran z-skor. Lebih jauh lagi, semua perhitungan ini dilakukan tanpa biaya transaksi. Jika faktor-faktor ini diperhitungkan, strategi ini pasti akan berkinerja buruk. Baik biaya maupun selisihnya saat ini belum ditentukan. Selain itu, strategi ini diperdagangkan dalam unit pecahan ETF, yang juga sangat tidak realistis.

Pada artikel mendatang, kami akan membuat backtester berbasis peristiwa yang lebih kompleks yang akan memperhitungkan semua hal di atas, sehingga memberi kami keyakinan lebih pada kurva ekuitas dan indikator kinerja kami.