Perdagangan berpasangan merupakan contoh yang bagus untuk mengembangkan strategi perdagangan berdasarkan analisis matematika. Dalam artikel ini, kami akan menunjukkan cara memanfaatkan data untuk membuat dan mengotomatiskan strategi perdagangan berpasangan.

Prinsip dasar

Misalkan Anda memiliki sepasang investasi X dan Y yang memiliki beberapa korelasi mendasar, seperti kedua perusahaan memproduksi produk yang sama, seperti Pepsi dan Coca-Cola. Anda ingin rasio harga atau dasar (juga disebut spread) antara keduanya tetap konstan dari waktu ke waktu. Namun, selisih antara kedua pasangan mata uang tersebut dapat berbeda sewaktu-waktu akibat perubahan permintaan dan penawaran yang bersifat sementara, seperti pesanan beli/jual dalam jumlah besar untuk satu target investasi, reaksi terhadap berita penting tentang salah satu perusahaan, dll. Dalam kasus ini, satu investasi bergerak ke atas dan investasi lainnya bergerak ke bawah relatif satu sama lain. Jika Anda memperkirakan divergensi ini akan kembali normal seiring berjalannya waktu, Anda dapat melihat peluang perdagangan (atau peluang arbitrase). Peluang arbitrase semacam itu ada di mana-mana di pasar mata uang digital atau pasar berjangka komoditas domestik, seperti hubungan antara BTC dan aset safe haven; hubungan antara bungkil kedelai, minyak kedelai, dan varietas kedelai dalam kontrak berjangka.

Bila terjadi perbedaan harga sementara, perdagangan akan menjual investasi yang berkinerja lebih baik (investasi yang naik) dan membeli investasi yang berkinerja lebih buruk (investasi yang turun). Anda dapat yakin bahwa ada perbedaan antara kedua investasi tersebut. spread pada akhirnya akan tercermin dari investasi yang berkinerja lebih baik yang jatuh kembali atau investasi yang berkinerja buruk yang naik kembali, atau keduanya. Perdagangan Anda akan menghasilkan uang dalam semua skenario ini. Jika investasi bergerak naik atau turun bersamaan tanpa mengubah selisih di antara keduanya, Anda tidak akan mendapat untung atau rugi uang.

Oleh karena itu, perdagangan berpasangan adalah strategi perdagangan netral pasar yang memungkinkan pedagang untuk mengambil keuntungan dari hampir semua kondisi pasar: tren naik, tren turun, atau menyamping.

Jelaskan konsepnya: dua target investasi hipotetis

• Membangun lingkungan penelitian kami di Platform Kuantitatif Inventor

Pertama-tama, agar dapat bekerja dengan lancar, kita perlu membangun lingkungan penelitian kita. Dalam artikel ini, kita menggunakan Inventor Quantitative Platform (FMZ.COM) untuk membangun lingkungan penelitian, terutama agar kita dapat menggunakan API yang nyaman dan cepat. antarmuka dan enkapsulasi platform ini nanti. Sistem Docker yang lengkap.

Dalam nama resmi Inventor Quantitative Platform, sistem Docker ini disebut sistem host.

Untuk informasi lebih lanjut tentang cara menyebarkan host dan robot, silakan lihat artikel saya sebelumnya: https://www.fmz.com/bbs-topic/4140

Pembaca yang ingin membeli host penyebaran server komputasi awan mereka sendiri dapat merujuk ke artikel ini: https://www.fmz.com/bbs-topic/2848

Setelah berhasil menerapkan layanan komputasi awan dan sistem host, kami akan menginstal alat Python paling kuat: Anaconda

Untuk mencapai semua lingkungan program relevan yang diperlukan untuk artikel ini (perpustakaan dependen, manajemen versi, dll.), cara termudah adalah menggunakan Anaconda. Ini adalah ekosistem ilmu data Python dan manajer ketergantungan yang dikemas.

Untuk metode instalasi Anaconda, silakan lihat panduan resmi Anaconda: https://www.anaconda.com/distribution/

Artikel ini juga akan menggunakan numpy dan pandas, dua pustaka yang sangat populer dan penting dalam komputasi ilmiah Python.

Untuk pekerjaan dasar di atas, Anda juga dapat merujuk ke artikel saya sebelumnya, yang memperkenalkan cara menyiapkan lingkungan Anaconda dan dua pustaka numpy dan pandas. Untuk detailnya, silakan lihat: https://www.fmz.com/digest- topik/4169

Selanjutnya, mari kita gunakan kode untuk mengimplementasikan “dua target investasi hipotetis”

import numpy as np
import pandas as pd

import statsmodels
from statsmodels.tsa.stattools import coint
# just set the seed for the random number generator
np.random.seed(107)

import matplotlib.pyplot as plt

Ya, kami juga akan menggunakan matplotlib, pustaka grafik yang sangat terkenal di Python.

Mari kita buat aset investasi hipotetis X dan simulasikan pemetaan pengembalian hariannya menggunakan distribusi normal. Kami kemudian melakukan penjumlahan kumulatif untuk mendapatkan nilai X harian.

# Generate daily returns
Xreturns = np.random.normal(0, 1, 100) 
# sum them and shift all the prices up
X = pd.Series(np.cumsum(
    Xreturns), name='X') 
    + 50
X.plot(figsize=(15,7))
plt.show()

Target investasi X, simulasikan dan gambarkan pengembalian hariannya melalui distribusi normal

Sekarang kita hasilkan Y yang berkorelasi kuat dengan X, jadi harga Y akan bergerak sangat mirip dengan perubahan pada X. Kami memodelkannya dengan mengambil X, menggesernya ke atas, dan menambahkan beberapa gangguan acak yang diambil dari distribusi normal.

noise = np.random.normal(0, 1, 100)
Y = X + 5 + noise
Y.name = 'Y'
pd.concat([X, Y], axis=1).plot(figsize=(15,7))
plt.show()

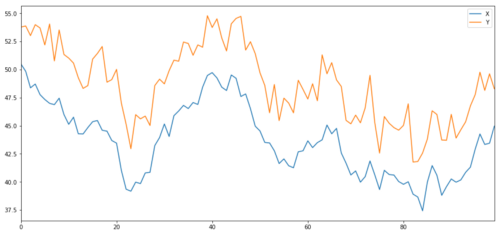
Mengintegrasikan target investasi X dan Y

Kointegrasi

Kointegrasi sangat mirip dengan korelasi, yang berarti bahwa rasio antara dua seri data akan bervariasi di sekitar nilai rata-rata. Dua seri Y dan X mengikuti yang berikut:

Y = ⍺ X + e

di mana ⍺ adalah rasio konstan dan e adalah noise.

Untuk pasangan perdagangan antara dua deret waktu, nilai rasio yang diharapkan dari waktu ke waktu harus konvergen ke nilai rata-rata, yaitu keduanya harus terkointegrasi. Rangkaian waktu yang kami buat di atas saling terintegrasi. Sekarang kita akan menggambar skala antara keduanya sehingga kita dapat melihat seperti apa tampilannya.

(Y/X).plot(figsize=(15,7)) 
plt.axhline((Y/X).mean(), color='red', linestyle='--') 
plt.xlabel('Time')
plt.legend(['Price Ratio', 'Mean'])
plt.show()

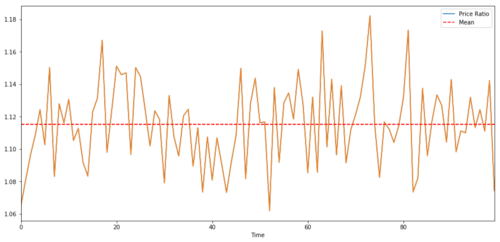
Rasio dan rata-rata harga dua investasi yang terkointegrasi

Uji Kointegrasi

Cara mudah untuk mengujinya adalah dengan menggunakan statsmodels.tsa.stattools. Kita seharusnya melihat nilai p yang sangat rendah karena kita secara artifisial membuat dua rangkaian data yang saling berkointegrasi semaksimal mungkin.

# compute the p-value of the cointegration test
# will inform us as to whether the ratio between the 2 timeseries is stationary
# around its mean
score, pvalue, _ = coint(X,Y)
print pvalue

Hasilnya adalah: 1.81864477307e-17

Catatan: Korelasi dan Kointegrasi

Walaupun korelasi dan kointegrasi serupa dalam teori, keduanya tidaklah sama. Mari kita lihat contoh rangkaian data yang berkorelasi tetapi tidak terkointegrasi, dan sebaliknya. Pertama mari kita periksa korelasi seri yang baru saja kita buat.

X.corr(Y)

Hasilnya adalah: 0,951

Seperti yang kami duga, ini sangat tinggi. Namun bagaimana dengan dua seri yang berkorelasi tetapi tidak terkointegrasi? Contoh sederhananya ialah dua rangkaian data yang berbeda.

ret1 = np.random.normal(1, 1, 100)
ret2 = np.random.normal(2, 1, 100)

s1 = pd.Series( np.cumsum(ret1), name='X')
s2 = pd.Series( np.cumsum(ret2), name='Y')

pd.concat([s1, s2], axis=1 ).plot(figsize=(15,7))
plt.show()
print 'Correlation: ' + str(X_diverging.corr(Y_diverging))
score, pvalue, _ = coint(X_diverging,Y_diverging)
print 'Cointegration test p-value: ' + str(pvalue)

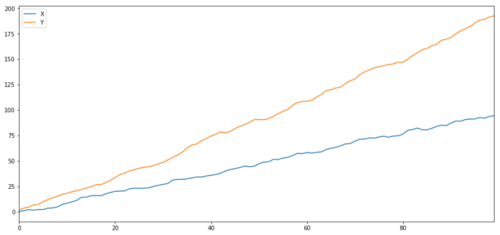
Dua seri terkait (tidak terintegrasi)

Koefisien korelasi: 0,998 Nilai p uji kointegrasi: 0,258

Contoh sederhana dari kointegrasi tanpa korelasi adalah seri yang terdistribusi normal dan gelombang persegi.

Y2 = pd.Series(np.random.normal(0, 1, 800), name='Y2') + 20
Y3 = Y2.copy()

Y3[0:100] = 30
Y3[100:200] = 10
Y3[200:300] = 30
Y3[300:400] = 10
Y3[400:500] = 30
Y3[500:600] = 10
Y3[600:700] = 30
Y3[700:800] = 10
Y2.plot(figsize=(15,7))
Y3.plot()
plt.ylim([0, 40])
plt.show()
# correlation is nearly zero
print 'Correlation: ' + str(Y2.corr(Y3))
score, pvalue, _ = coint(Y2,Y3)
print 'Cointegration test p-value: ' + str(pvalue)

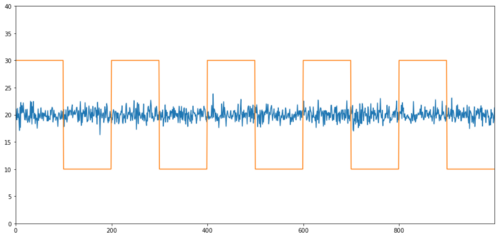
Korelasi: 0,007546 Nilai p uji kointegrasi: 0,0

Korelasinya sangat rendah, tetapi nilai p menunjukkan kointegrasi yang sempurna!

Bagaimana cara melakukan perdagangan berpasangan?

Karena dua deret waktu yang terkointegrasi (seperti X dan Y di atas) bergerak mendekati dan menjauhi satu sama lain, ada saatnya terdapat basis tinggi dan basis rendah. Kami melakukan perdagangan berpasangan dengan membeli satu investasi dan menjual investasi lainnya. Dengan cara ini, jika dua target investasi turun atau naik bersamaan, kami tidak menghasilkan uang maupun kehilangan uang, dengan kata lain, kami netral pasar.

Kembali ke X dan Y di Y = ⍺ X + e di atas, kita menghasilkan uang dengan membuat rasio (Y/X) bergerak di sekitar nilai rata-ratanya ⍺. Untuk melakukan ini, kita perhatikan bahwa ketika X Ketika nilai ⍺ terlalu tinggi atau terlalu rendah, nilai ⍺ terlalu tinggi atau terlalu rendah:

• Rasio Panjang: Ini terjadi saat rasio ⍺ kecil dan kita memperkirakan rasio tersebut akan menjadi lebih besar. Pada contoh di atas, kita membuka posisi dengan mengambil posisi long Y dan short X.

• Rasio Pendek: Ini terjadi ketika rasio ⍺ besar dan kita memperkirakan rasionya akan menjadi lebih kecil. Pada contoh di atas, kita membuka posisi dengan melakukan short selling pada Y dan melakukan long selling pada X.

Perlu dicatat bahwa kita selalu memiliki “posisi lindung nilai”: jika posisi long yang mendasarinya kehilangan nilai, posisi short menghasilkan uang, dan sebaliknya, jadi kita kebal terhadap pergerakan pasar secara keseluruhan.

Saat aset X dan Y bergerak relatif satu sama lain, kita menghasilkan uang atau kehilangan uang.

Gunakan data untuk menemukan transaksi dengan perilaku serupa

Cara terbaik untuk melakukan ini adalah memulai dengan perdagangan yang Anda curigai mungkin terkointegrasi dan melakukan uji statistik. Jika Anda melakukan uji statistik pada semua pasangan perdagangan, Anda akanBias perbandingan gandakorban dari.

Bias perbandingan gandamengacu pada situasi di mana peluang menghasilkan nilai-p signifikan secara palsu meningkat ketika menjalankan banyak pengujian, karena kita perlu menjalankan sejumlah besar pengujian. Jika kita menjalankan pengujian ini 100 kali pada data acak, kita akan melihat 5 nilai p di bawah 0,05. Jika Anda membandingkan n instrumen untuk kointegrasi, Anda akan melakukan perbandingan n(n-1)/2 dan Anda akan melihat banyak nilai-p yang salah, yang akan meningkat seiring dengan peningkatan ukuran sampel uji Anda. Dan meningkat. Untuk menghindari hal ini, pilih beberapa pasangan perdagangan yang menurut Anda mungkin terkointegrasi, lalu uji pasangan tersebut satu per satu. Ini akan sangat mengurangiBias perbandingan ganda。

Jadi mari kita coba temukan beberapa instrumen yang menunjukkan kointegrasi. Mari kita ambil sekeranjang saham teknologi berkapitalisasi besar AS di S&P 500. Instrumen-instrumen ini beroperasi di segmen pasar yang sama dan menunjukkan kointegrasi. harga. Kami memindai daftar instrumen perdagangan dan menguji kointegrasi antara semua pasangan.

Matriks skor uji kointegrasi yang dikembalikan, matriks nilai-p, dan semua kecocokan berpasangan dengan nilai-p kurang dari 0,05 disertakan.Metode ini rentan terhadap bias perbandingan ganda, sehingga dalam praktiknya mereka perlu melakukan validasi kedua. Dalam artikel ini, demi kenyamanan penjelasan kami, kami memilih untuk mengabaikan hal ini dalam contoh.

def find_cointegrated_pairs(data):
    n = data.shape[1]
    score_matrix = np.zeros((n, n))
    pvalue_matrix = np.ones((n, n))
    keys = data.keys()
    pairs = []
    for i in range(n):
        for j in range(i+1, n):
            S1 = data[keys[i]]
            S2 = data[keys[j]]
            result = coint(S1, S2)
            score = result[0]
            pvalue = result[1]
            score_matrix[i, j] = score
            pvalue_matrix[i, j] = pvalue
            if pvalue < 0.02:
                pairs.append((keys[i], keys[j]))
    return score_matrix, pvalue_matrix, pairs

Catatan: Kami telah memasukkan tolok ukur pasar (SPX) dalam data kami - pasar menggerakkan aliran banyak instrumen dan sering kali Anda mungkin menemukan dua instrumen yang tampaknya terkointegrasi; tetapi sebenarnya mereka tidak terkointegrasi satu sama lain, tetapi Kointegrasi dengan pasar. Ini disebut variabel pengganggu. Penting untuk memeriksa partisipasi pasar dalam hubungan apa pun yang Anda temukan.

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2007/12/01'
endDateStr = '2017/12/01'
cachedFolderName = 'yahooData/'
dataSetId = 'testPairsTrading'
instrumentIds = ['SPY','AAPL','ADBE','SYMC','EBAY','MSFT','QCOM',
                 'HPQ','JNPR','AMD','IBM']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
data = ds.getBookDataByFeature()['Adj Close']
data.head(3)

Sekarang mari kita coba mencari pasangan perdagangan yang terkointegrasi menggunakan metode kami.

# Heatmap to show the p-values of the cointegration test
# between each pair of stocks
scores, pvalues, pairs = find_cointegrated_pairs(data)
import seaborn
m = [0,0.2,0.4,0.6,0.8,1]
seaborn.heatmap(pvalues, xticklabels=instrumentIds, 
                yticklabels=instrumentIds, cmap=’RdYlGn_r’, 
                mask = (pvalues >= 0.98))
plt.show()
print pairs

[('ADBE', 'MSFT')]

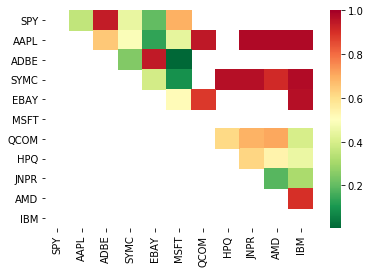
Tampaknya ‘ADBE’ dan ‘MSFT’ saling terintegrasi. Mari kita lihat harganya untuk memastikan apakah harganya masuk akal.

S1 = data['ADBE']
S2 = data['MSFT']
score, pvalue, _ = coint(S1, S2)
print(pvalue)
ratios = S1 / S2
ratios.plot()
plt.axhline(ratios.mean())
plt.legend([' Ratio'])
plt.show()

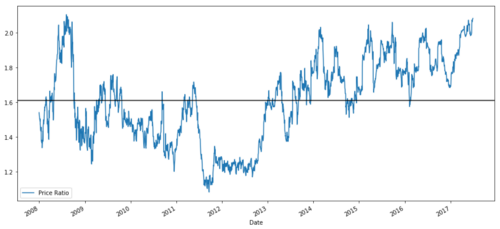
Grafik rasio harga antara MSFT dan ADBE dari tahun 2008 hingga 2017

Rasio ini tampak seperti rata-rata yang stabil. Rasio absolut tidak terlalu berguna secara statistik. Lebih membantu untuk menormalkan sinyal kita dengan melihatnya sebagai skor-z. Skor Z didefinisikan sebagai:

Z Score (Value) = (Value — Mean) / Standard Deviation

memperingatkan

Dalam praktik, kami biasanya mencoba menerapkan beberapa perluasan pada data, tetapi hanya jika datanya terdistribusi normal. Namun, banyak data keuangan yang tidak terdistribusi normal, jadi kita harus sangat berhati-hati untuk tidak sekadar berasumsi kenormalan atau distribusi tertentu saat membuat statistik. Distribusi rasio yang sebenarnya mungkin memiliki ekor yang gemuk, dan data yang cenderung ke arah ekstrem dapat membingungkan model kita dan menyebabkan kerugian yang besar.

def zscore(series):
    return (series - series.mean()) / np.std(series)

zscore(ratios).plot()
plt.axhline(zscore(ratios).mean())
plt.axhline(1.0, color=’red’)
plt.axhline(-1.0, color=’green’)
plt.show()

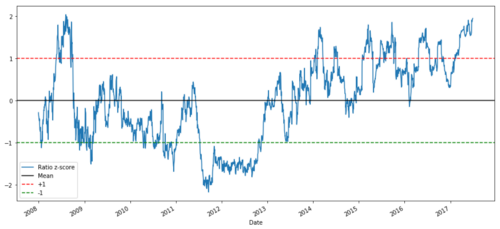
Rasio Harga Z antara MSFT dan ADBE dari tahun 2008 hingga 2017

Sekarang lebih mudah untuk melihat bagaimana rasio bergerak di sekitar rata-rata, tetapi kadang-kadang cenderung memiliki penyimpangan besar dari rata-rata, yang dapat kita manfaatkan.

Setelah kita membahas dasar-dasar strategi perdagangan berpasangan dan mengidentifikasi target kointegrasi berdasarkan riwayat harga, mari kita coba mengembangkan sinyal perdagangan. Pertama, mari kita tinjau langkah-langkah untuk mengembangkan sinyal perdagangan menggunakan teknik data:

• Mengumpulkan data yang dapat diandalkan dan membersihkan data

• Buat fungsi dari data untuk mengidentifikasi sinyal/logika perdagangan

• Fitur dapat berupa rata-rata pergerakan atau data harga, korelasi atau rasio sinyal yang lebih kompleks - gabungkan ini untuk membuat fitur baru

• Gunakan fitur ini untuk menghasilkan sinyal perdagangan, yaitu sinyal mana yang merupakan posisi beli, jual, atau pendek

Untungnya, kami memiliki Inventor Quantitative Platform (fmz.com) untuk melengkapi keempat aspek di atas bagi kami. Ini adalah berkah yang luar biasa bagi para pengembang strategi. Kami dapat menggunakan energi dan waktu kami untuk logika strategi, desain, dan perluasan fungsional.

Pada Inventor Quantitative Platform, terdapat paket antarmuka dari berbagai bursa utama. Yang perlu kita lakukan hanyalah memanggil antarmuka API ini. Logika implementasi yang mendasarinya telah disempurnakan oleh tim profesional.

Demi kelengkapan logis dan penjelasan prinsip, kami akan menyajikan logika dasar ini secara terperinci, tetapi dalam pengoperasian sebenarnya, pembaca dapat langsung memanggil antarmuka API Inventor Quant untuk melengkapi keempat aspek di atas.

Mari kita mulai:

Langkah 1: Siapkan masalah Anda

Di sini kita mencoba membuat sinyal yang memberi tahu kita apakah rasio tersebut akan membeli atau menjual pada saat berikutnya, yang merupakan variabel prediktor Y:

Y = Ratio is buy (1) or sell (-1)

Y(t)= Sign(Ratio(t+1) — Ratio(t))

Perlu dicatat bahwa kita tidak perlu memprediksi harga sebenarnya dari aset dasar, atau bahkan nilai sebenarnya dari rasio tersebut (meskipun kita bisa), kita hanya perlu memprediksi arah rasio berikutnya.

Langkah 2: Kumpulkan data yang andal dan akurat

Inventor Quant adalah teman Anda! Anda cukup menentukan instrumen yang ingin Anda perdagangkan serta sumber data yang ingin Anda gunakan, dan aplikasi akan mengekstrak data yang diperlukan serta membersihkannya untuk pembagian dividen dan instrumen. Jadi data kami di sini sudah sangat bersih.

Kami menggunakan data berikut dari Yahoo Finance untuk hari perdagangan selama 10 tahun terakhir (sekitar 2.500 titik data): buka, tutup, tinggi, rendah, dan volume

Langkah 3: Memisahkan data

Jangan lupakan langkah yang sangat penting ini untuk menguji keakuratan model Anda. Kami menggunakan pemisahan data pelatihan/validasi/pengujian berikut

• Training 7 years ~ 70%

• Test ~ 3 years 30%

ratios = data['ADBE'] / data['MSFT']
print(len(ratios))
train = ratios[:1762]
test = ratios[1762:]

Idealnya, kami juga akan membuat set validasi, tetapi kami tidak akan melakukannya untuk saat ini.

Langkah 4: Rekayasa Fitur

Apa saja fungsi terkaitnya? Kami ingin memprediksi arah perubahan rasio. Kita telah melihat bahwa kedua instrumen kita terkointegrasi, sehingga rasio ini akan cenderung bergeser dan kembali ke rata-rata. Tampaknya fitur kita harus berupa pengukuran rata-rata rasio, dan perbedaan antara nilai saat ini dan rata-ratanya dapat menghasilkan sinyal perdagangan kita.

Kami menggunakan fungsi berikut:

• Rasio Rata-rata Pergerakan 60 Hari: Ukuran rata-rata pergerakan

• Rasio Rata-rata Pergerakan 5 Hari: Ukuran nilai rata-rata pergerakan saat ini

• Deviasi standar 60 hari

• Skor z: (MA 5 hari - MA 60 hari) / SD 60 hari

ratios_mavg5 = train.rolling(window=5,
                               center=False).mean()
ratios_mavg60 = train.rolling(window=60,
                               center=False).mean()
std_60 = train.rolling(window=60,
                        center=False).std()
zscore_60_5 = (ratios_mavg5 - ratios_mavg60)/std_60
plt.figure(figsize=(15,7))
plt.plot(train.index, train.values)
plt.plot(ratios_mavg5.index, ratios_mavg5.values)
plt.plot(ratios_mavg60.index, ratios_mavg60.values)
plt.legend(['Ratio','5d Ratio MA', '60d Ratio MA'])
plt.ylabel('Ratio')
plt.show()

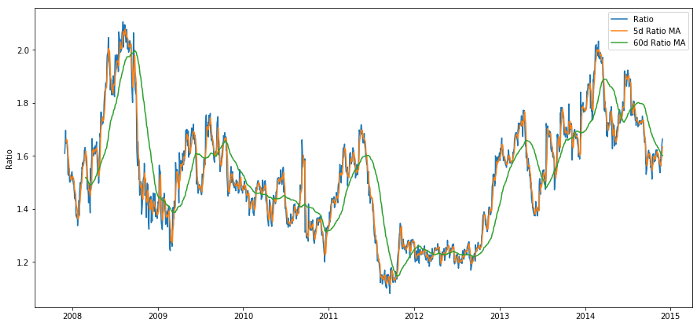
Rasio harga MA 60d dan 5d

plt.figure(figsize=(15,7))
zscore_60_5.plot()
plt.axhline(0, color='black')
plt.axhline(1.0, color='red', linestyle='--')
plt.axhline(-1.0, color='green', linestyle='--')
plt.legend(['Rolling Ratio z-Score', 'Mean', '+1', '-1'])
plt.show()

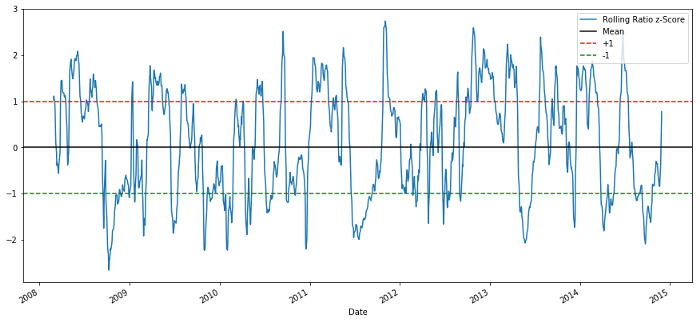
Rasio Harga Z-score 60-5

Skor Z dari rata-rata bergulir benar-benar menunjukkan sifat rasio yang berbalik arah!

Langkah 5: Pemilihan model

Mari kita mulai dengan model yang sangat sederhana. Dengan melihat grafik z-skor, kita dapat melihat bahwa setiap kali z-skor terlalu tinggi atau terlalu rendah, ia akan mengalami kemunduran. Mari kita gunakan +1/-1 sebagai ambang batas kita untuk menentukan terlalu tinggi dan terlalu rendah, lalu kita dapat menggunakan model berikut untuk menghasilkan sinyal perdagangan:

• Ketika z dibawah -1.0 maka rasionya adalah beli (1) karena kita mengharapkan z kembali ke 0, sehingga rasionya meningkat

• Ketika z di atas 1.0, rasionya adalah jual (-1) karena kita mengharapkan z kembali ke 0, sehingga menurunkan rasionya

Langkah 6: Pelatihan, Validasi, dan Optimasi

Terakhir, mari kita lihat dampak sebenarnya dari model kita terhadap data nyata? Mari kita lihat bagaimana sinyal ini berperilaku dalam rasio nyata

# Plot the ratios and buy and sell signals from z score
plt.figure(figsize=(15,7))
train[60:].plot()
buy = train.copy()
sell = train.copy()
buy[zscore_60_5>-1] = 0
sell[zscore_60_5<1] = 0
buy[60:].plot(color=’g’, linestyle=’None’, marker=’^’)
sell[60:].plot(color=’r’, linestyle=’None’, marker=’^’)
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,ratios.min(),ratios.max()))
plt.legend([‘Ratio’, ‘Buy Signal’, ‘Sell Signal’])
plt.show()

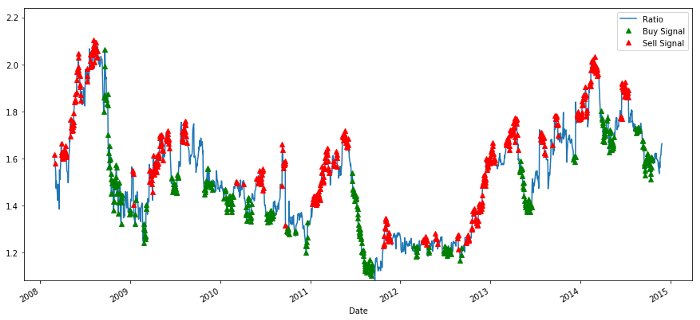
Sinyal Rasio Harga Beli dan Jual

Sinyal ini nampaknya masuk akal, kita cenderung menjual rasio ketika rasionya tinggi atau meningkat (titik merah) dan membelinya kembali ketika rasionya rendah (titik hijau) dan menurun. Apa artinya ini bagi subjek sebenarnya dari transaksi kita? Mari kita lihat

# Plot the prices and buy and sell signals from z score
plt.figure(figsize=(18,9))
S1 = data['ADBE'].iloc[:1762]
S2 = data['MSFT'].iloc[:1762]
S1[60:].plot(color='b')
S2[60:].plot(color='c')
buyR = 0*S1.copy()
sellR = 0*S1.copy()
# When buying the ratio, buy S1 and sell S2
buyR[buy!=0] = S1[buy!=0]
sellR[buy!=0] = S2[buy!=0]
# When selling the ratio, sell S1 and buy S2 
buyR[sell!=0] = S2[sell!=0]
sellR[sell!=0] = S1[sell!=0]
buyR[60:].plot(color='g', linestyle='None', marker='^')
sellR[60:].plot(color='r', linestyle='None', marker='^')
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,min(S1.min(),S2.min()),max(S1.max(),S2.max())))
plt.legend(['ADBE','MSFT', 'Buy Signal', 'Sell Signal'])
plt.show()

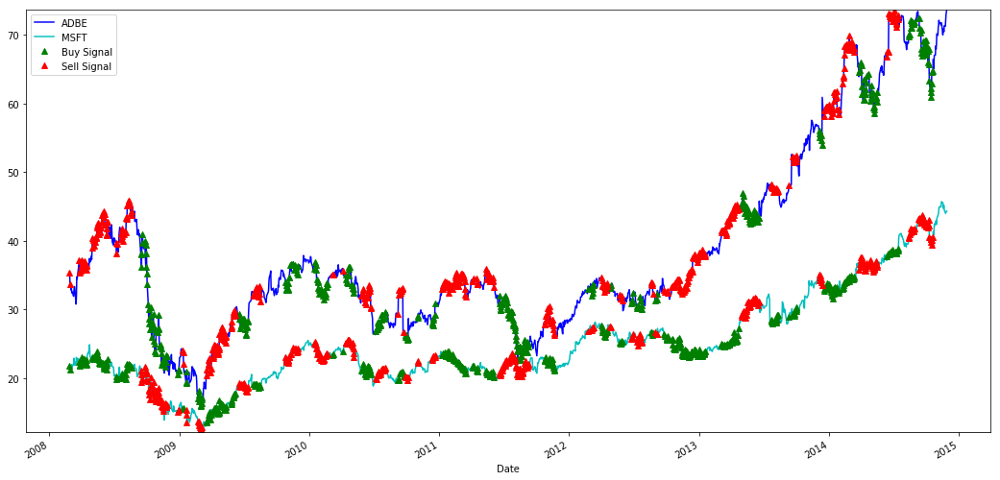
Sinyal untuk membeli dan menjual saham MSFT dan ADBE

Perhatikan bagaimana kita terkadang menghasilkan uang dari “short leg”, terkadang dari “long leg”, dan terkadang keduanya.

Kami senang dengan sinyal data pelatihan. Mari kita lihat berapa banyak keuntungan yang dapat dihasilkan dari sinyal ini. Kita dapat membuat backtester sederhana yang membeli 1 rasio (membeli 1 saham ADBE dan menjual rasio x saham MSFT) ketika rasionya rendah dan menjual 1 rasio (menjual 1 saham ADBE dan rasio panggilan x saham MSFT) dan menghitung perdagangan PnL untuk ini. rasio.

# Trade using a simple strategy
def trade(S1, S2, window1, window2):
    
    # If window length is 0, algorithm doesn't make sense, so exit
    if (window1 == 0) or (window2 == 0):
        return 0
    
    # Compute rolling mean and rolling standard deviation
    ratios = S1/S2
    ma1 = ratios.rolling(window=window1,
                               center=False).mean()
    ma2 = ratios.rolling(window=window2,
                               center=False).mean()
    std = ratios.rolling(window=window2,
                        center=False).std()
    zscore = (ma1 - ma2)/std
    
    # Simulate trading
    # Start with no money and no positions
    money = 0
    countS1 = 0
    countS2 = 0
    for i in range(len(ratios)):
        # Sell short if the z-score is > 1
        if zscore[i] > 1:
            money += S1[i] - S2[i] * ratios[i]
            countS1 -= 1
            countS2 += ratios[i]
            print('Selling Ratio %s %s %s %s'%(money, ratios[i], countS1,countS2))
        # Buy long if the z-score is < 1
        elif zscore[i] < -1:
            money -= S1[i] - S2[i] * ratios[i]
            countS1 += 1
            countS2 -= ratios[i]
            print('Buying Ratio %s %s %s %s'%(money,ratios[i], countS1,countS2))
        # Clear positions if the z-score between -.5 and .5
        elif abs(zscore[i]) < 0.75:
            money += S1[i] * countS1 + S2[i] * countS2
            countS1 = 0
            countS2 = 0
            print('Exit pos %s %s %s %s'%(money,ratios[i], countS1,countS2))
            
            
    return money
trade(data['ADBE'].iloc[:1763], data['MSFT'].iloc[:1763], 60, 5)

Hasilnya adalah: 1783.375

Jadi strategi ini tampaknya menguntungkan! Sekarang, kita dapat mengoptimalkan lebih lanjut dengan mengubah jendela waktu rata-rata bergerak, dengan mengubah ambang batas untuk posisi beli/jual dan penutupan, dsb. dan memeriksa peningkatan kinerja pada data validasi.

Kita juga dapat mencoba model yang lebih kompleks seperti Regresi Logistik, SVM, dll. untuk prediksi 1/-1.

Sekarang, mari kita lanjutkan model ini, yang membawa kita ke

Langkah 7: Uji ulang data pengujian

Di sini saya ingin menyebutkan Inventor Quantitative Platform. Platform ini menggunakan mesin pengujian ulang QPS/TPS berkinerja tinggi untuk benar-benar mereproduksi lingkungan historis, menghilangkan perangkap pengujian ulang kuantitatif yang umum, dan segera menemukan kekurangan strategi, sehingga dapat memberikan hasil nyata yang lebih baik. - investasi waktu. Tawarkan bantuan.

Untuk menjelaskan prinsip tersebut, artikel ini memilih untuk menunjukkan logika yang mendasarinya. Dalam penerapan praktis, pembaca disarankan untuk menggunakan Inventor Quantitative Platform. Selain menghemat waktu, yang penting adalah meningkatkan tingkat toleransi kesalahan.

Pengujian ulang itu mudah. ​​Kita dapat menggunakan fungsi di atas untuk melihat PnL dari data pengujian.

trade(data[‘ADBE’].iloc[1762:], data[‘MSFT’].iloc[1762:], 60, 5)

Hasilnya adalah: 5262.868

Model ini dibuat dengan sangat baik! Ini menjadi model perdagangan berpasangan sederhana pertama kami.

Hindari overfitting

Sebelum saya mengakhiri, saya ingin berbicara khusus tentang overfitting. Overfitting adalah jebakan paling berbahaya dalam strategi perdagangan. Algoritma overfitting mungkin berkinerja sangat baik dalam pengujian ulang tetapi gagal pada data baru yang belum terlihat - artinya ia tidak benar-benar mengungkapkan tren apa pun dalam data dan tidak memiliki daya prediksi yang nyata. Mari kita ambil contoh sederhana.

Dalam model kami, kami menggunakan estimasi parameter bergulir dan berharap dapat mengoptimalkan panjang jendela waktu. Kita mungkin memutuskan untuk sekadar mengulangi semua kemungkinan, jangka waktu yang wajar, dan memilih jangka waktu berdasarkan model kita yang berkinerja terbaik. Di bawah ini kami menulis loop sederhana untuk menilai panjang jendela waktu berdasarkan PNL data pelatihan dan menemukan loop terbaik.

# Find the window length 0-254 
# that gives the highest returns using this strategy
length_scores = [trade(data['ADBE'].iloc[:1762], 
                data['MSFT'].iloc[:1762], l, 5) 
                for l in range(255)]
best_length = np.argmax(length_scores)
print ('Best window length:', best_length)

('Best window length:', 40)

Sekarang kita periksa kinerja model pada data uji, dan kita lihat bahwa panjang jendela waktu ini jauh dari optimal! Hal ini karena pilihan awal kami jelas melebihi data sampel.

# Find the returns for test data
# using what we think is the best window length
length_scores2 = [trade(data['ADBE'].iloc[1762:], 
                  data['MSFT'].iloc[1762:],l,5) 
                  for l in range(255)]
print (best_length, 'day window:', length_scores2[best_length])
# Find the best window length based on this dataset, 
# and the returns using this window length
best_length2 = np.argmax(length_scores2)
print (best_length2, 'day window:', length_scores2[best_length2])

(40, 'day window:', 1252233.1395)
(15, 'day window:', 1449116.4522)

Jelas apa yang berhasil dengan baik untuk data sampel kita tidak selalu menghasilkan hasil yang baik di masa mendatang. Hanya untuk pengujian, mari kita plot skor panjang yang dihitung dari dua set data

plt.figure(figsize=(15,7))
plt.plot(length_scores)
plt.plot(length_scores2)
plt.xlabel('Window length')
plt.ylabel('Score')
plt.legend(['Training', 'Test'])
plt.show()

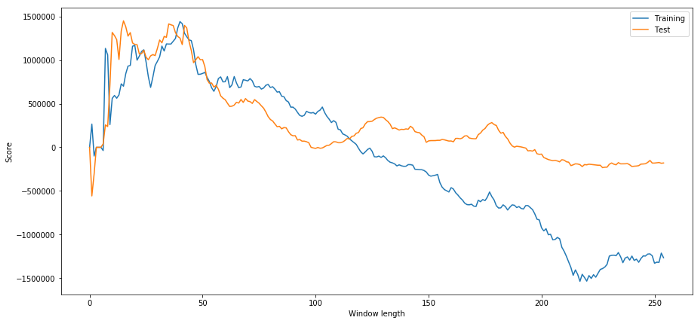
Kita dapat melihat bahwa angka antara 20-50 merupakan pilihan yang baik untuk jangka waktu tersebut.

Untuk menghindari overfitting, kita dapat menggunakan penalaran ekonomi atau properti algoritma untuk memilih panjang jendela waktu. Kita juga dapat menggunakan filter Kalman, yang tidak mengharuskan kita menentukan panjangnya; metode ini akan dibahas nanti di artikel lain.

Langkah selanjutnya

Dalam artikel ini, kami menyajikan beberapa metode pengantar sederhana untuk menunjukkan proses pengembangan strategi perdagangan. Dalam praktiknya, statistik yang lebih canggih harus digunakan, dan Anda dapat mempertimbangkan opsi berikut:

• Eksponen Hurst

• Waktu paruh pembalikan rata-rata disimpulkan dari proses Ornstein-Uhlenbeck

• Saringan Kalman