この記事では,Ornstein-Uhlenbeck プロセスを概説し,その数学式を記述し,Python で実装し,模擬し,定量金融とシステム取引におけるいくつかの実用的なアプリケーションについて議論する.より高度なランダムなプロセスモデル,Ornstein-Uhlenbeck (OU) プロセスと呼ばれるモデルを使用して,均等値の帰帰帰行動を示す回帰時間序列をモデル化するために使用することができる.これは,派生品の定価における利率のモデル化と,取引時のシステム取引に対してアルゴリズムを実行するのに特に有用である.

オーンシュタイン-ウレンベックプロセスは?

Ornstein-Uhlenbeck過程は,平均値帰帰帰の行動をモデル化するために使用される連続時間ランダム化過程である.これは,無限漂移できる標準的なランダムな漂流やブラウン運動とは異なり,OU過程は,時間の経過とともに長期平均値に回復する傾向があることを意味する.数学的に言えば,OU過程は,この均等値帰の行動を制御する特定のランダム微分方程式 (SDE) の解である.OU過程のSDEは,次の式で与えられる.

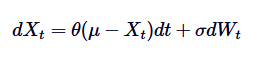
その中で,Xtは時間tにおけるランダムな過程を表し,μは長期平均値,θは平均値帰帰率,δは波動性であり,dWtはウィーナー過程または標準ブラウン運動である.

歴史的背景と応用

オルンシュタイン-ウレンベック法は,最初にレオナルド・オルンシュタインとジョージ・ユージン・ウレンベックによって1930年に提案され,摩擦のある条件下でブラウン運動を行う粒子の速度を模擬するために用いられた.時間とともに,その実用性は,物理学を超えて,生物学,化学,経済学,金融学など,さまざまな分野に応用されている.

定量金融において,OUプロセスは平均値帰帰帰の現象をモデル化するのに特に有用である.顕著な例は,利率,為替レート,金融市場の変動性である.例えば,一般的な利率モデルであるVasicekモデルは,OUプロセスから直接推論されている.

量子金融における重要性

オーンシュタイン-ウレンベックプロセスは,以下のような理由で量金融において重要である.その平均値回帰性により,金融変数のモデリングの自然な選択となる.これらの金融変数は,ランダムな移動行為を示すのではなく,安定した長期平均値の波動を中心に振動する.この特性は,利率モデリングにおいて,利率回帰は,中央銀行の長期安定利率への影響を反映する.

さらに,OUプロセスは,資産価格モデル (derivative valuation を含む) とリスク管理戦略にも用いられる.コックス・イングルソル・ロス (CIR) モデルなど,より複雑なモデルの構成要素として用いられる.このモデルは,OUプロセスを,負でない利率のモデル化に拡張する.

主要な特徴と直感

オーンシュタイン-ウレンベックプロセスの主な特徴は以下の通りである.

• 平均回帰はOU プロセスは長期平均値に回帰する傾向がある.これは,ブラウン運動などのプロセスとは対照的に,後者はそのような傾向を示していない.
• 変動性:参数δ 制御過程におけるランダム性または波動性のレベル.波動性が高いほど,プロセスが回帰前に平均値から偏るほど大きい.
• 戻り速度:参数θは,プロセスが平均値に戻る速度を決定する.θ値が高くなるほど,平均値に戻る速度が速い.
• 安定性:OU プロセスは平坦であり,つまりその統計的性質は時間とともに変化しないことを意味する.これは金融分野における安定システムのモデリングに不可欠である.

直観的に言えば,Ornstein-Uhlenbeck過程を平均値の周りに伸びる皮筋の行動をモデル化すると考えることができる。この過程はランダムな波動によって平均値から偏る可能性があるが,皮筋の拉力 (平均値の回帰に似たもの) は,それが最終的に平均値に戻ることを保証する。

他のランダムなプロセスとの比較

OU プロセスは,様々な金融現象のモデリングと密接に関連しているため,しばしば他のランダムなプロセス (例えば,ブラウン運動や幾何学的なブラウン運動 (GBM)) と比較される.ブラウン運動とは異なり (ブラウン運動は平均値への帰還の傾向がない),OU プロセスは,平均値への帰還の明らかな行動を有する.これは,変数が安定した均衡の波動の周りに存在するシナリオをモデリングするのにより適している.

通常,株価のモデル化に使用され,漂移と波動の項を含むGBMと比較して,OUプロセスは指数的な成長を示さないが,その平均値の振動を中心に表現する.GBMは,時間とともに増加する数値のモデル化に適しているが,OUプロセスは,平均値の回帰特性を示す変数のモデル化に適している.

量子金融の例として

Ornstein-Uhlenbecプロセスは,金融分野において,特に平均値帰帰帰が重要な特徴であるモデリングのシナリオにおいて,広範な応用がある. 以下では,最も一般的な使用例について議論する.

利率モデリング

OUプロセスの最も顕著な応用の一つは,特にヴァシチェクモデルの枠組みの中で,利率のモデリングである.ヴァシチェクモデルは,利率がOUプロセスを従うことを仮定し,すなわち,利率は時間とともに長期平均値に戻る傾向がある.この特性は,利率の行動を正確にシミュレートするために重要である.なぜなら,利率は無限期に波動するのではなく,経済条件の影響による平均水準の近くで波動する傾向があるからである.

資産の価格

資産の価格,特に固定利益証券において,OUプロセスは通常,債券の利回りの進化を模倣するために使用されます.OUプロセスの平均値回帰性により,利回りは,その歴史的平均値からあまりにも遠く離れないことを保証し,これは観察された市場行動と一致します.これは,OUプロセスを債券および他の利率敏感なツールの価格設定の貴重なツールにします.

配合取引戦略

配合取引は,市場中立の戦略であり,関連資産の2つの間で抵消ポジションを確立することを含む.この場合,OUプロセスは,通常は平均回帰である2つの資産の価格差をモデル化できるため,特に有用である.OUプロセスの使用により,価格差をモデル化することにより,トレーダーは,価格が平均値から偏っているときに,利益の入場と出口を確認し,平均回帰を予測し,取引シグナルを生成することができます.

例えば,2つの期貨の価格差が,ある値下げを超えて拡大すると,トレーダーは,優れたパフォーマンスを発揮する期貨を空売りし,不良なパフォーマンスを発揮する期貨を多額に購入し,価格差が歴史的平均水準に戻ることを期待し,逆転が起こると利益を得ることができる.

オーンシュタイン-ウレンベック SDEの解

Ornstein-Uhlenbeck過程の微分方程式公式は,その解の基礎である.このSDEを解くために,積分因数法を使用している.SDEを書き換える.

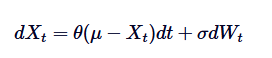
まず,両辺を 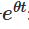の積分因数で掛けます.

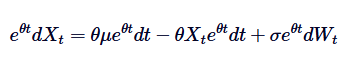
注意してください,両側に 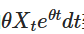を加えた場合,左側は,乗積の差として表現できます.

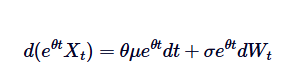
この2つの辺を0からtに積分すると,

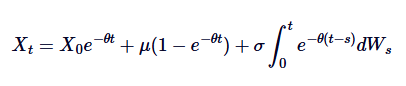
これは,Ornstein-Uhlenbeck SDEの一般的な解である.

上述で推論された明示的な解決にはいくつかの重要な意味がある。第一項 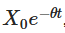は,初期値が時間とともに衰退し,そのプロセスがどのように徐々にその出発点を忘れるかを示している。第二項 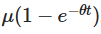は,プロセスが時間とともに平均微値に傾きつつあることを示している。第三項は,ランダム性を導入し,その中でWienerのプロセスの積分がランダム波動を説明している。

この解決法は,確定平均回帰行動とブラウン運動駆動のランダム分数の間のバランスを強調している.この解決法を理解することは,OUプロセスを効果的にシミュレートするために不可欠であり,以下のように説明されている.

他のランダムなプロセスとの関連

Ornstein-Uhlenbeckプロセスは,他の有名なランダムなプロセス (ブラウン運動とヴァシケックモデルを含む) といくつかの重要な関連性を持っています.

ブラウン運動との関係

Ornstein-Uhlenbeck過程は,ブラウン運動の平均回帰バージョンであると考えられる.ブラウン運動は,独立増量で平均回帰のない傾向を記述する過程であり,OU過程は,ドリフト項を使用してブラウン運動を修正して平均回帰を導入し,その結果,過程を中心値に戻す.数学的に言えば,θ=0と設定すると,OU過程は,波動帯の標準ブラウン運動に簡略化される:

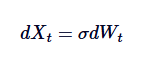
したがって,ブラウン運動はOU過程の特殊例であり,平均値回帰の欠落に対応する.

ヴァシケックモデルとの関係

Vasicekモデルは,利率モデリングに広く用いられ,本質的に利率の進化におけるOrnstein-Uhlenbeckプロセスの適用である.Vasicekモデルは,利率がOUプロセスに従うことを仮定し,SDEは以下のように定義される.

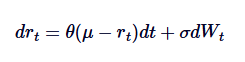
その中で,rtは短期利率を表し,パラメータθ,μ,δの解釈は,OU過程における解釈に似ています.ヴァシチェクモデルは,平均値帰帰利率経路を生成できるので,金融モデリングにおける主要な優位性の一つである.

これらの関係を理解することで,OUプロセスが様々な環境で,特に金融分野での使用方法についてより広く理解できます. 応用例については,以下で説明します.

PythonでOrnstein-Uhlenbeckプロセスを模擬する

このセクションでは,PythonでOrnstein-Uhlenbeck (OU) プロセスを模擬する方法について説明します.これは,OUプロセスを定義するランダム微分方程式 (SDE) を分散化するために,Euler-Maruyamaの分散化を使用することになります.

SDEの分散化

SDEの数学式を振り返り,各項目を概要として見ていきましょう.

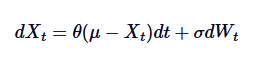
で、

• Xtは,t時間におけるプロセスの値である.
• θは平均値の回帰速度である.
• μはプロセスの長期平均値である.
• δは波動率の参数である.
• dWtは,ウィーナー過程 (標準ブラウン運動) の増加を表している.

このプロセスをコンピュータで模擬するには,連続時間SDEを分散化する必要がある.よく使われる方法の一つは,Euler-Maruyama分散化で,小さな散時間ステップを考慮して連続プロセスを近似する.Ornstein-Uhlenbeckプロセスの散形は以下の式で与えられる.

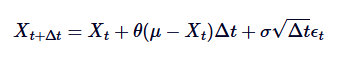
その中で, 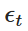は,標準正規分布から抽出したランダム変数である (すなわち, 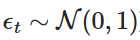).この分散化により,時間とともに Xt の値を繰り返し計算することができ,それによって OU プロセスの振る舞いを模倣することができる.

Pythonの実装

では,Pythonで Ornstein-Uhlenbeck プロセスの分散化を実装してみましょう. ここでは,NumPyとMatplotlib Python ライブラリのみを使用します.

まず,標準的な方法でNumPyとMatplotlibをインポートします. 次に,OUモデルにすべてのパラメータを指定します. 次に,OUの経路を計算した後にそれに追加するために,長さNのNumPy配列を事前に割り当てます. 次に,N−1のステップを代します (ステップ1は初期条件X0が指定されています),ランダム増量dWを模擬し,次にOUの経路の次の代を上記の数学式に基づいて計算します. 最後に,Matplotlibを使用して経路の履歴を描きます.

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 10.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

グラフは以下の通りです.

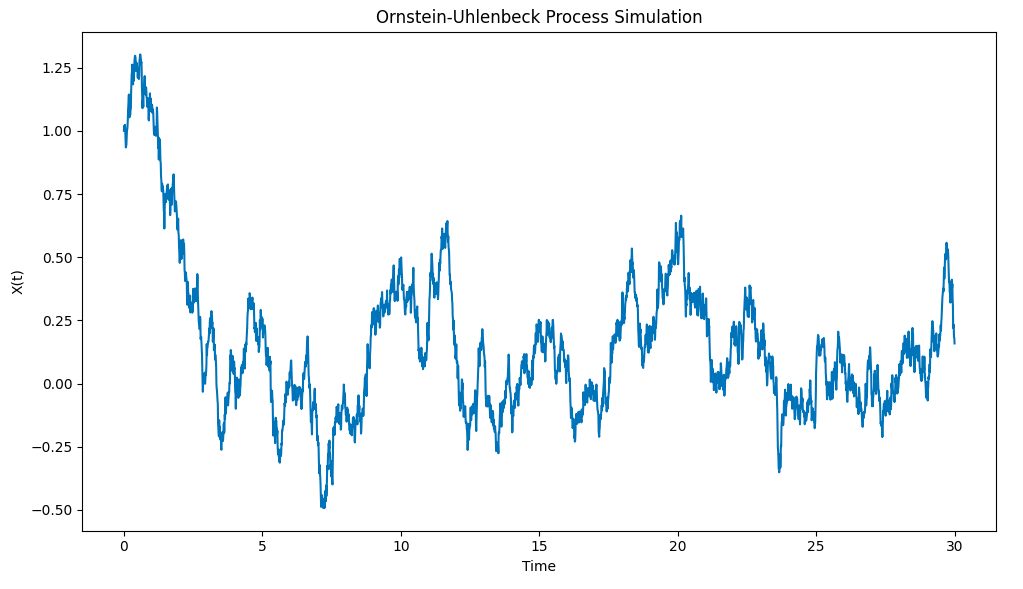
Pythonで描いたOrnstein-Uhlenbeckプロセスのシミュレーション

このプロセスが初期条件からX0=1のを平均値μ=0まで素早くり,それからその平均値から逸れたとき,その平均値に戻る傾向を示していることに注意してください.

結論と後続

この記事では,Ornstein-Uhlenbeck プロセスを概説し,その数学的公式を記述し,連続時間 SDE を模擬する Python の基本的な実装を提供しました. 次の記事では,OU プロセスに基づいて構築されたより複雑な SDE を研究し,それらのシステム取引とデリバティブ価格設定のアプリケーションで使用する方法について説明します.

完全なコード

# OU process simulation

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 30.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

元の記事へのリンク:https://www.quantstart.com/articles/ornstein-uhlenbeck-simulation-with-python/