いくつかのプログラマティック取引モデルのパラメータを最適化する方法についてお話ししましょう

• #### 参数高原と参数孤島

　 参数最適化における重要な原則は,参数孤島ではなく,参数高原を目指すことである.いわゆる参数高原は,より広い参数範囲が存在することを指し,モデルはこの参数範囲で優れた効果が得られる.一般的には,高原の中心でほぼ正規分布形を形成する.いわゆる参数孤島は,参数値が非常に小さな範囲にある場合にのみ,モデルが良好なパフォーマンスを発揮することを指し,参数値がこの値から偏った場合,モデルのパフォーマンスは著しく変化する.

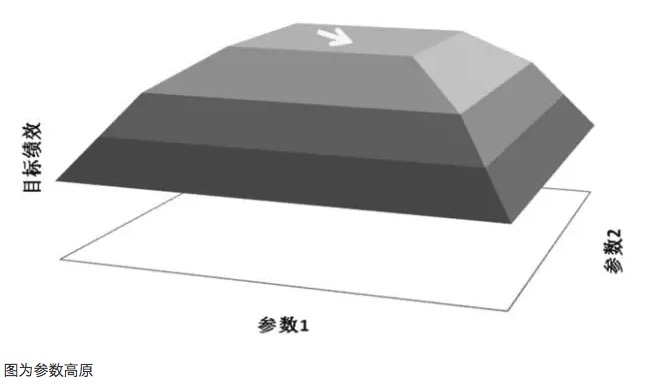
• #### パラメータ高原

参数高原図と参数孤島図を例に挙げると,ある取引モデルの内には2つの参数,それぞれ参数1と参数2があるとする.その2つの参数に巡回テストを行った後,3次元パフォーマンス図が得られる.良いパラメータ分布は参数高原図であるべきであり,たとえ参数設定が偏移したとしても,モデルの収益性パフォーマンスは依然として保証される.このような参数安定性が強いため,モデルが将来実務で様々な状況に遭遇する際には,強い因果能力を持つことができる.しかし,参数孤島図のような参数巡回後のパフォーマンスの結果,パラメータが小さな偏移の時に,モデルの収益性が大きく変化する場合は,このようなパラメータの適応因子性能は,現実取引の多くの変化する市場環境に対応することが困難である.

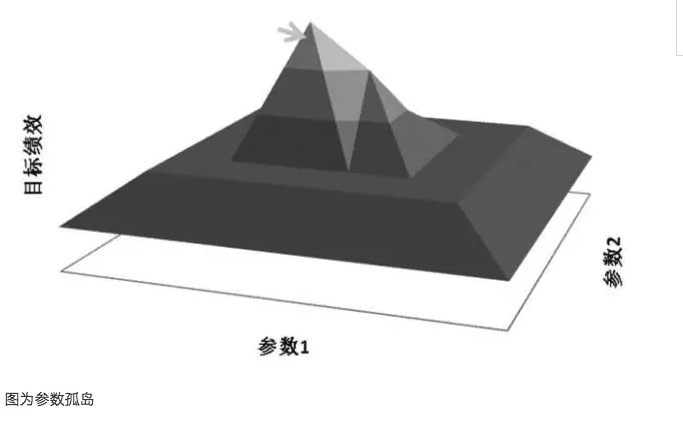
一般的に,近辺のパラメータシステムの性能が最適パラメータの性能よりはるかに劣っている場合,この最適パラメータは,過積和の結果である可能性があり,数学的には奇点解であると考えられるが,求められる極大値解ではない.数学的に,奇点は不安定であり,将来の不確実な状況において,市場特性が変化すれば,最適パラメータは最低パラメータに変わる可能性がある.

過適合は,選択されたサンプルと関係している.選択されたサンプルが市場全体の特性を表さない場合,テスト結果が正の期待値に達するためにだけパラメータを調整する.この行為は,自欺瞞である.得られたパラメータ値は,過適合の有効なパラメータ値である.例えば,パラメータ過適合を分析することによって,取引モデルでは,それぞれ35と63の値で収益率の突破現象が起こります.モデル内の相応の指標が35と63のパラメータとして選択された場合,モデルの収益は完璧に見えますが,実際には典型的なパラメータ孤島効果です.

過適合とパラメータ最適化の主な矛盾は,モデルパラメータ最適化によって得られる最適パラメータは,すでに起こった歴史的データサンプルのみに基づいており,将来の動向は動的に変化し,歴史的動向と比較して類似性も変異性もあるということである.モデル設計者は,モデルが歴史的に最もよくやったパラメータを見つけることができるが,このパラメータは,将来のモデルの実際のアプリケーションで必ずしも最もよくやったわけではない.さらに,歴史的に最もよくやったモデルパラメータは,将来のモデルの実戦で非常に悪いパフォーマンスを発揮するパラメータであり,大きな損失をもたらす可能性がある.例えば,歴史の大きな動きを捉えたパラメータを1つ選択したモデルを,そのようなパラメータ値で設定したモデルは,モデルが将来の戦闘でこれほどうまく機能することを意味しない.この歴史的に優れたパラメータ値は,おそらく将来のモデルに適用されるのに何の助けにもならない.

さらに,パラメータ高原とパラメータ孤島は往々にして取引回数と大きな関係がある.モデルが取引回数少ない場合,適切なパラメータポイントを見つけることがよくあり,そのためモデルはこの数回の取引で利益を得ることができる.このパラメータ最適化後のモデルの利益は,より強い偶然性を表している.モデルが取引回数多い場合,モデルの利益の偶然性は低下し,利益の必然性と規則性をより多く表している.また,パラメータ高原が存在する.このパラメータ最適化モデルは,パラメータ最適化の目的である.

• #### パラメータを最適化する方法

参数高原と参数孤島を理解した後,最適化参数の手法は重要であることが明らかになる.特にモデルに複数の参数がある場合 (以下参数数列) において,しばしば1つの参数値の取付は,別の参数高原の分布に影響を与える.それでは,参数数列の最適化はどうすればよいのでしょうか.

一つの方法は,段階的収束法である。すなわち,まず1つのパラメータを個別に最適化して,その最適値を取得した後に固定され,次に別のパラメータを最適化して,その最適値を取得した後に固定され。そうして,最適化結果は変化しないまで循環する。例えば,均線交差取引モデルでは,二つの独立したパラメータは,均線短周期N1と長周期N2である。最初にN2を1と固定し,N1を1から100の数値範囲でテストフィルターし,最適値を探し,最終的に最適値が8と固定される;次にN2を1から200の間で最適化して,最適値が26と固定される;再びN1を2回目の最適化で,新しい最適値10と固定される;最後にN2を最適化して,最適値28と固定される。そして,こうして,サイクルフィルターの下では,最適化結果は変化しないまで,最適化結果は変化しない。例えば,最終的なパラメータの最小値が10,N1からN2と30の数値になる場合,この作業は終了する。

別の方法は,強力な計算機能を持つプログラム化されたソフトウェア設計プラットフォームを利用して,ターゲット関数とパラメータの配列の間の配分を直接計算し,多次元差分配分を探し,差分絶対値が値範囲より小さい差分値を定義し,対応する多次元体積の最大,多次元内切球半径の最高を,最も安定したパラメータ値として選択する.

パラメータ最適化方法に加えて,データサンプリングも重要な要因である.トレンドを追跡するトレンドアイデアのモデルは,トレンドの動きが起こる時にうまく機能し,高い価格で低い価格で取引するトレンドアイデアの戦略は,振動の動きでうまく機能する.したがって,パラメータ最適化では,取引の考えに合致する動きを適切に排除して利益を考慮し,戦略に合致しない考えに合致しない動きのデータを考慮して損失を考慮する.

株価指数期貨を例に挙げると,上場初の2010年および極端な大牛市情勢の発生した2014年後半から現在まで,株価指数期貨は単面的な行事である.すべてのトレンドモデルが良い結果をもたらすことは間違いない.しかし,この極端な行事データのサンプルにパラメータ最適化を加えた場合,得られるモデルパラメータは必ずしも最適ではない.

例えば,あるモデルに2つのパラメータがあると仮定すると,パラメータAのテスト結果は,片側行情時間段では非常に良い効果をあげ,他の時間段では一般的であった.別のパラメータBのテスト結果は,片側行情時間段ではパラメータAより劣った効果をあげ,他の時間段ではパラメータAよりも優れていた.各時間段間の分布は,パラメータAと均等であった.パラメータAが,サンプルデータ全体でテストされたリスク・リターンなどの総合指標が,パラメータBよりも高かったとしても,パラメータBが比較的に安定し,特定のサンプルに依存しないため,パラメータBを選ぶ傾向がある.

要するに,プログラム化された取引モデルを構築する際には,一方では,パラメータ最適化によってモデルを改良して,価格変動のパターンにモデルをより良く適応させ,投資収益を向上させることができる.一方では,パラメータ最適化に過度に適合して,市場状況の変化に対するモデルの適応性が大幅に低下することを防ぐことも必要である.

プログラム化されたトレーダー