女の子を追いかけてミサイルを見つける - ベイズ統計

• ### ONE

情緒が解らない死理主義者は,情緒的な生活の中で必ずこのような悲嘆の場面に遭遇する:偶然,心地よい美しい女の子に出会って,その日から,昼夜考え,眠り忘れ食物をし,長い暗恋の旅を始め,終わりのない絡み合いの中で,ついに勇気を集めて少女に告白する日を待って,結果,少女の”私はすでに彼氏を持っている”という言葉は天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才のように天才

女の子が独身かどうか正確に判断する方法は,このような不快な事態を避けるために,必修の科目になっています.

女の子と一緒に仕事をして,しばしば彼女のそばにいて,彼女が独身かどうかを知ることは難しい問題ではない.しかし,死理主義者の達成すべき難題は,少女と距離を置く見知らぬ人として,少女が気づかないままに,手の届く限られた情報で少女の独身状況を判断できるというものです.それだけでなく,死理主義者の追求の結果は一定に定量化され,計算された独身の確率mmは2桁の小数値も保持する必要があります.

方法はこのように:第一歩,直感を信じなさい。死理派は,何人か友人を集めて,秘密裏に標的の女の子を観察することを考えてもよい,当然,探す人は死理派である必要はない,どんな心情診断チーム,噂の粉砕機,自然制御,刑事医は何人かを見つけるのがよい,既婚者,情景の老人,花の盗賊は,何人か探すのもよい,人数が多くなるほど,人数が多くなるほど,人数が多くなるほど,人数が多くなるほど,人数が多くなるほど,人数が多くなるほど,人数が多くなるほど,人数が多くなるほど,人数が多くなるほど,人数が多くなるほど,人数が多くなるほど,人数が多くなるほど,人数が多くなるほど,人数が多くなるほど,人数が多くなるほど,人数が多くなるほど,人数が多くなるほど,人数が多くなるほど,人数が多くなるほど,人数が多くなるほど,人数が多くなるほど,人数が多くなるほど,人数が多くなるほど,人数が多くなるほど,人数が多くなるほど,人数が多くなるほど,人数が多く

投票者の個人的な経験や感情によって得られた結果で,死理主義者の客観的な理性のやり方と一致しているところは何でしょうか? そのために,私たちは事実と証拠で話す第二のステップを行います.

科学的な研究のように,まず資料を調べて,Googleで検索すると,多くの孤独な人が長年潜伏して研究してきたシンプルで使いやすい独身の識別基準を見つけることができます.例えば,携帯電話の原則 (恋愛中の女の子は携帯電話の使用頻度が比較的に高い),自習の原則 (独身の女の子は,多くの場合,数人の女の子と自習している) など.その後,身の回りで,独身の女の子の群れについて統計的実験をしてみて,もちろん,サンプルが大きければ大きいほど,得られます.

統計値などです

これらの実験のデータが揃った後,私たちは,ちょうど投票した65.65%の確率値を修正し,最適化する作業を進めることができます.何に依存しているのでしょうか?それは,様々な基準のターゲット女の子のパフォーマンスです.例えば,ターゲットMMが友達と自習に行くことを好むことを発見し,自分の統計の調査結果によると,すでに恋愛しているMMの女の子のうち,友達と自習に行くことを好む女の子は約60%を占めています.恋愛していない女の子のうち,友達と自習に行くことを好む女の子は約30%を占めています.

単身の確率は,

死にかけている人の心の中で, 暗に喜びを感じているに違いない.

単身の女の子では,携帯電話の使用率が1.2回/時間以上で20%を占めるが,恋愛中の女の子では,この値は60%である. 対象の女の子は,携帯電話の使用率が1.2回/時間以上であることが観察され,確率結果は更新されます.

この回,シングル確率は56.02%に悲劇的に下がった.死理主義者は,より多くの評価基準を捜し,より多くの研究を行い,少女のシングル確率はどんどん事実に近づくように更新し続けることができます.しかし,最終的な結果を得る前に,あなたは最初に値値を設定する必要があります:少女のシングル確率は,この値値を上回ります (例えば90%),あなたは腕時計を告白する価値があります,そうでなければ,あなたは直接死ぬでしょう.

しかし,注意すべきは,数回計算しても,結果として得られるのは確率値であり,事実ではなく,たとえ何度もの研究を経て,対象の女の子の独身確率は99.9%と確定されていても,すぐに彼女に告白する準備ができている.しかし,女の子の最後の観察研究で,男性と女の子の手を握って笑ったり,抱擁したりすると,女の子の独身確率は99.9%から0に近づくことになる.

この記事では,この判断の科学的で厳格な死理的方法がベイエス統計方法と呼ばれる.ベイエス法は,単純に,先入観の確率+新しい証拠=修正後の確率というもので,情報量に制限されず,主観的な判断と限られた客観的な情報を含む様々なソースの結果を統合して,最終的な結論を得ることができる.ここでは,この方法には一定のリスクがあり,試す際には注意が必要であり,小児は試さないようにと厳格に宣言する.

しかし,死理主義者が発明したベイズの法則は無視すべきではない.アメリカ海軍は,失われたヒルゲン爆弾や,失われた核潜水艦を,洋で捜索するために,この方法を用いた.

• ### TWO

1966年1月のある日,アメリカ合衆国のB-52爆撃機がスペインのパロマレス上空を飛んだ.その機内の数人のパイロットが,空軍司令部が彼らに割り当てた空中給油任務を遂行していた.この飛行は理屈的に危険とは言えない.パイロットは,非常に穏やかな人であり,飛行機の飛行でも,大きなパイプの2つのポンプを吸うことは決して好きではないと言われている.しかし,この会議の機長と彼の何人かの部下は,大きなトラブルに遭遇し,その後大きなパイプの利用をやめることは難しい.

悲劇と喜劇の連続が続きます.

失われたヒルゲン爆弾を捜すために,アメリカ合衆国は国内から,多くの専門家からなる捜索部隊を急いで現場に派遣した.その中には,ジョン・クレイヴンという名前の数学者も含まれていた.その名前の由来は,アメリカ海軍特別計画局の首席科学者のという名前だった.それが特別であるなら,それは一般的ではない.クレイヴン博士の仕事は,何が特別なのか?

弾の探求に関して,クレイブンの提案は,前述のベイエス手法を用いて,各分野の専門家を集め,しかし,各専門家が自分の専門分野を持っていることは通用ではない.B-52の爆弾について多くのことがわかっているが,弾の特性についてはほとんど知られていない.弾が飛行機にどのように保管されているか,弾が飛行機からどのように落ちるか,弾が航空機の残骸と一緒になるかどうか,答えも出ていない.弾の2つの降落がそれぞれ開く確率は?風の流れと方向?弾が地面に落下すると土に埋まるのか.

この様々な問題に対して,クレイブンは専門家たちに様々な仮説を立て,様々なシナリオを想像し,それから,様々な状況下で,各位置に弾が置かれる確率と,それぞれの状況での可能性を推測するよう求めました.

Cravenの方法も同僚の疑問に遭った.彼の計画では,結果の多くは,これらの専門家が推測,投票,賭博の形で得られたため,すべての結果の正確性を保証することはできません.しかし,爆弾の捜索の任務は緊急であり,正確な実験を行い,完全な信頼できる理論を確立する時間はありませんので,Cravenの方法は,実行可能な方法である.

専門家からを募った結果を得て,それをまとめて,爆弾の位置の確率図を描いた:可能性のある全領域を多くの小方形に分割し,各小方形には異なる確率値があり,高低があり,地図上の山頂と谷の等しい高線のように.少女が独身かどうかを判断する理性主義者と同様に,クラヴェンはベイアスの方法の第一歩を完了した.

その後,クレーブと捜索隊の指揮官は,クレーブの捜索を開始し,検索の過程で同時に各格子の確率を更新した.しかし,最も確率の高い格子の位置が,陸上の険しい峡谷と深海地帯で示されることが多い.クレーブは実際にそこにあったとしても,見つけることは不可能であるため,クレーブはすでにそこにあることを示す別の確率図を描画する必要があり,クレーブの位置の確率ではなく,クレーブの位置の確率を示す.

わずか2年後,1968年に,クレイブンは再び才能を発揮する機会を得て,小さな弾を再び失い,アメリカ海軍は大きな弾を再び失いました.

1968年6月,海軍の天号核潜水艦が大西洋アジア海域で突然失踪し,潜水艦と船上の99人の海軍士官兵は全員音信がなくなりました.事後調査報告書によると,犯人は,この潜水艦の奇妙なトーレールで,発射された後に敵に敵意を示し,自らを向かい,潜水艦の内弾を爆発させました.

スウェン号の位置を探すため,アメリカ海軍は大規模な捜索を実施し,クレイヴンも自然にそれに参加した.事故時の潜水艦の航行速度が遅いため,方向,爆発の衝撃の大きさの方向,爆発時の潜水艦の方向は不明であり,潜水艦が爆発した場所を知っていても,潜水艦の残骸が最終的に海水に浸かされた場所を特定するのは難しい.クレイヴンは,半径20マイルの円圏内の海底で,スウェン潜水艦がそこに横たわっている可能性があることを初心的に推定し,これほど広い範囲で,これほど深い海底で潜水艦を見つけるのはほとんど不可能である.

事故の前後に潜水艦に何が起こったのか正確に推測できる専門家はいないが,ヒルゲン爆弾の捜索時と同様に,Cravenは数学者,潜水艦の専門家,海上捜索の各分野の専門家と協議し,あらゆる可能なヒルゲン脚本を作成し,彼らの知識と経験に基づいて,状況がどの方向に発展するか推測するようにした. 枯燥した作業に少しの趣味を加えるために,Cravenはウィスキーボトルを準備し,ヒルゲンが正しいことを賭けた賞品として準備したと言われている.

最後に,クラヴェンは20マイル海域の確率図を得た.海域全体が多くの小格子に分けられ,各小格子には2つの確率値pとqがある.pは潜水艦がこの格子の中に横たわっている確率で,qは潜水艦がこの格子の中にいる場合,探査された確率である.経験的に,第二の確率値は,海域の水深と関係しており,深海地域を探索する際に失敗した潜水艦が網を漏らす可能性はより大きい.もし格子の一つが探査された後,潜水艦の痕跡が見つからなかった場合,ベイエスの原理に従って更新された後,この格子潜水艦の存在の可能性は低下する.

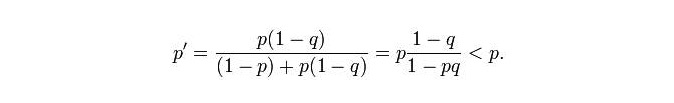
潜水艦が他の格子に存在する確率は上昇します.

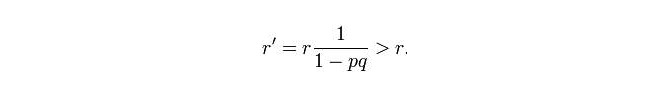
捜索ごとに,潜水艦が全域内で最も確率のある格子で検索を行う.もし発見されなかった場合,確率分布は一回洗い流され,捜索船は新しい格子で最も疑わしい格子に移動して検索を行う.天が発見されるまで,このまま下へ進む.

当初は,海軍は経験的に潜水艦が爆発地点の東側の海底にあると推定し,クレーブや他の数学者たちの提案を軽視したが,数ヶ月の捜索の結果は何も得られなかった.後に海軍は,クレーブンの提案に従わなければならなかった.概率図によると,事故後の潜水艦は爆発地点の西側にいたべきである.いくつかの捜索の後,潜水艦は爆発地点の南西の海底で発見された.

2回の強烈なパフォーマンスを受けて,Cravenが海事検索で使用したベイアス法は徐々に広く受け入れられ,それ以来,ベイアス法は意外と頻繁に弾,核潜水艦と共にキーワードとして至る所に登場した.数十年で,ベイアス法は,Googleの検索キーワードのフィルターから無人車の総合的な判断まで,自分の移動位置を判断するために,あらゆる角を掘り下げて,ますます広く適用されました.もちろん,この神奇な方法は,追女に実際に大小に使用されています.

アニール・ダ・マテマティクス・モデリングより