習得すべき7つの回帰分析テクニック

发明者量化-小小梦

1376

Followers

習得すべき7つの回帰分析テクニック

Quantpedia

Created 2016-12-18 10:22:43 Updated 2016-12-18 11:08:56

3678

習得すべき7つの回帰分析テクニック

この記事は,回帰分析とその優位性を説明し,重点的に,習得すべき線形回帰,論理回帰,多項式回帰,漸進回帰,<unk>回帰,<unk>回帰,ElasticNet回帰など,最もよく使用される7つの回帰技術とその重要な要素をまとめ,最後に,正しい回帰モデルを選ぶための重要な要素を紹介している.
**
**
<unk>編成者ボタンの回帰分析は,データモデリングと分析の重要なツールである.この記事は,回帰分析の含意とその優位性を説明し,線形回帰,論理回帰,多項式回帰,漸進回帰,<unk>回帰,<unk>回帰,ElasticNet回帰などの7つの最も一般的に使用される回帰技術と,正しい回帰モデルを選択するための重要な要素を概要にまとめています.

逆帰分析とは何か?

回帰分析は,因数変数 ((目標)) と自変数 ((予測器)) の間の関係を研究する予測的モデリング技術である.この技術は,通常,予測分析,時間序列モデル,および発見変数間の因果関係に使用される.例えば,ドライバーの無謀な運転と道路交通事故の数の間の関係,研究する最良の方法は,回帰である.

還元分析は,データをモデル化および分析する重要なツールである。ここでは,曲線/線を使用して,これらのデータポイントを適合させ,この方法で,曲線または線からデータポイントまでの距離の差は最小限にします。私は,次の部分で詳細に説明します。
なぜリグレクション分析を使うのか?

上記のように,帰帰帰分析は,2つ以上の変数間の関係を推定する.以下,それを理解するために簡単な例を挙げます.

例えば,現在の経済状況では,会社の売上高の伸びを予測する. 現在,会社の最新データがあり,売上高の伸びは経済成長の2.5倍程度です. 回帰分析を使用すると,現在の情報と過去の情報を元に将来の会社の売上を予測できます.

還元分析を使用するメリットはいくつかあります.具体的には以下の通りです.

これは自変数と因変数の間の有意な関係を示している.

それは,複数の自変数が因変数に与える影響の強さを示している.

還元分析はまた,価格の変化とプロモーション活動の数の間の関連など,異なる尺度で測定される変数の間の相互作用を比較することを可能にします. これは,市場研究者,データ分析者,およびデータ科学者が予測モデルを構築するために最適な変数を排除し,推定するのを助けるのに役立ちます.
どれだけの回帰技術があるのでしょうか?

予測のために様々な回帰技術があります.これらの技術は主に3つの尺度 (自変数の個数,因変数の種類,および回帰線の形状) に基づいています.私たちは,下記のセクションでそれらを詳細に議論します.

独創的な人にとっては,上記のパラメータの組み合わせを使う必要があると感じた場合,使用されていない回帰モデルを作ることもできます. しかし,始める前に,最も一般的な回帰方法について説明しましょう.
- 1. 線形回帰
  
  最もよく知られているモデリング技術の一つである. 線形帰帰帰は,予測モデルを学ぶ際に通常,最も好まれる技術の一つである. この技術では,変数が連続であるため,自変数は連続である場合も,離散である場合もあり,帰帰線の性質は線形である.
  
  線形回帰は,最適合直線 ((すなわち回帰線) を使って因変数 ((Y) と自変数 ((X) のいずれかとの関係を確立する.
  
  これは,y=a+bという方程式です.*X + e で,a は切断,b は直線の傾き,e は誤差項である.この方程式は,与えられた予測変数 (s) に基づいて,ターゲット変数の値を予測することができる.
  
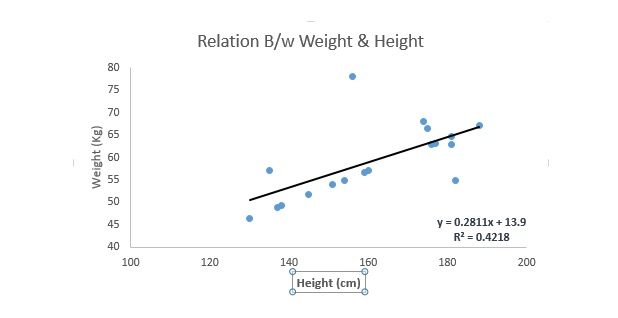
  一元線形回帰と多元線形回帰の違いは,多元線形回帰には ((>1) の自変数があり,一元線形回帰には通常は1つの自変数しか存在しないということです.今,問題は,どうやって最適の適合線を得るかということです.
  
  どれが最適合線 (a と b) の値になるか?
  
  この問題は最小二乗法で簡単に解決できる.最小二乗法も回帰線を適合させる最も一般的な方法である.観測データでは,各データ点の垂直偏差の二乗を線に合わせて最小化して最適適合線を計算する.偏差が二乗になるので,正値と負値は相殺されない.
  
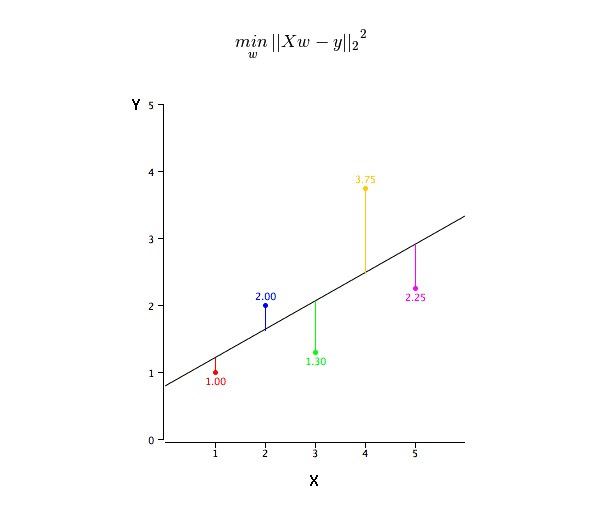
  R-square指標を使用してモデル性能を評価することができます.これらの指標の詳細については,以下を参照してください:モデル性能指標Part 1,Part 2 .
  
  ポイント:
  - 自変数と因数変数の間には,線形的な関係がある必要があります.
  - 多元回帰には多重共線性,自相関性,異方性がある.
  - 線形回帰は異常値に非常に敏感である。それは回帰線を大きく影響し,最終的には予測値に影響する。
  - 多重共線性により係数推定値の差が増加し,モデルがわずかに変化すると,推定は非常に敏感になる.結果として係数推定値は不安定になる.
  - 複数の自変数がある場合,前向き選択法,後向き削除法,そして段階的なフィルタリング法を使用して最も重要な自変数を選択することができます.
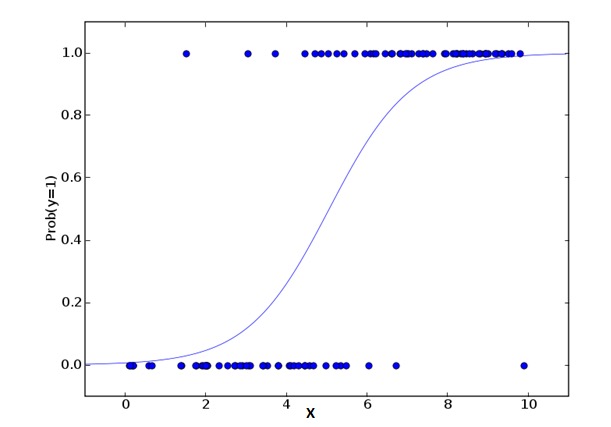
- 2. ロジスティック・リグレッション
  
  論理回帰は,<unk>事件=Success<unk>,<unk>事件=Failure<unk>の確率を計算するために用いられる.因数変数の型が二元 ((1/0,真/偽,イエス/ノー) の変数である場合,論理回帰を使用するべきである.ここでは,Yの値は0から1までであり,次の方程式で表現できる.
```
            
            
            
odds= p/ (1-p) = probability of event occurrence / probability of not event occurrence
ln(odds) = ln(p/(1-p))
logit(p) = ln(p/(1-p)) = b0+b1X1+b2X2+b3X3....+bkXk
```
  この式では,pが特定の特性を有する確率を表しています. 疑問に思うべきは,なぜlogを公式に使うのか?
  
  ここでは二項分布 ((因数変数) を使っているので,この分布に対して最適の連結関数を選ぶ必要がある。それはLogit関数である。上記の方程式では,サンプルを観察して極大似似合いを推定する値でパラメータを選択するのであり,平方と誤差を最小化するのではなく (一般回帰で用いられるように) である。
  
  ポイント:
  - これは分類の問題で広く用いられる.
  - 論理回帰は自変数と因変数が線形関係であることを要求しない。それは予測される相対リスク指数ORに対して非線形ログ変換を使用するため,様々な種類の関係に対応できる。
  - 超適合と不適合を避けるために,すべての重要な変数を含めるべきである。この状態を保証する良い方法がある.それは,段階的<unk>選方法を使用して論理回帰を推定することである。
  - 試料の量も大きいので,試料の数が少ない場合,非常に高い確率で推定される効果は,通常の最小二乗の倍数より劣る.
  - 自変数は相互に関連してはならない,すなわち多重共線性を持たない.しかしながら,分析およびモデリングでは,分類変数の相互作用の影響を含むことを選択することができます.
  - 因数変数の値が順序変数である場合,それを順序論理回帰と呼びます.
  - 変数が多種である場合,それを多元論理帰帰帰と呼びます.
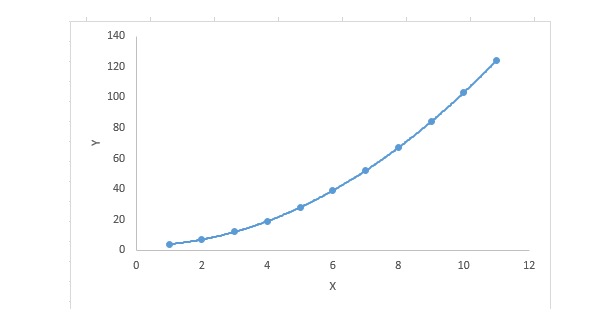
- 3. ポリノミアル回帰
  
  リグレーション方程式について,自変数の指数が1より大きい場合は,多項式リグレーション方程式である.以下の方程式で示される.
```
            
            
            
y=a+b*x^2
```
  この回帰技術では,最適合線は直線ではなく,データポイントを適合させるための曲線である.
  
  ポイント:
  - 高次多項式を適合させ,低誤差が得られる誘導があるが,これは過適合に繋がる可能性がある. 適合をよく見るために関係図を描き,過適合も欠適合もない合理的な適合を保証することに集中する必要がある. 以下は,理解するのに役立つ図である.
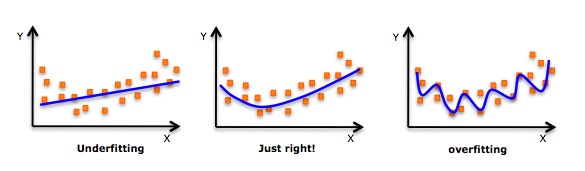
  - 明らかに両端の曲線点を探して,これらの形状や傾向が意味があるかどうかを見てください.より高い次元の多項式は,最終的に奇妙な推論結果を生じることがあります.
- 4. ステップ・ウィズ・レグレーション
  
  複数の自変数を扱うとき,この形式の帰帰帰を用いることができる.この技術では,自変数の選択は,非人為操作を含む自動化されたプロセスで行われます.
  
  この偉業は,R-square,t-stats,およびAIC指標のような統計的値を見て,重要な変数を識別することです. 漸進回帰は,指定された基準に基づく相関変数を同時に追加/削除することによってモデルに適合します. 以下は,最もよく使用される漸進回帰方法のいくつかです.
  - 標準漸進回帰法では,2つのことを行います.すなわち,各ステップに必要な予測を追加したり削除したりします.
  - 前進選択は,モデルの中で最も顕著な予測から始まり,そして各ステップに変数を追加する.
  - 後方<unk>除法では,すべての予測とモデルを同時に開始し,次に,各ステップで最小の有意な変数を排除する.
  - このモデリング技術は,最小限の予測変数を用いて予測能力を最大化することを目的としている.これは,高次元データセットを扱う方法の1つです.
- 5. リッジ回帰
  
  <unk>回帰分析は,多重共線性 (自変数高度関連) が存在するデータに使用される技術である.多重共線性では,最小二乗法 (OLS) が各変数に対して公平であるにもかかわらず,それらの差異は大きいので,観測値が偏移し,真価から遠く離れている.<unk>回帰は,帰帰推定に偏差を1つ加えることで標準誤差を低減する.
  
  線形回帰方程式は,次のようになります.
```
            
            
            
y=a+ b*x
```
  この方程式にも誤差項があります. 完全な方程式は:
```
            
            
            
y=a+b*x+e (error term),  [error term is the value needed to correct for a prediction error between the observed and predicted value]
=> y=a+y= a+ b1x1+ b2x2+....+e, for multiple independent variables.
```
  線形方程式では,予測誤差は2つの分数に分解できる。一方は偏差,一方は方差。予測誤差は,この2つの分数またはこの2つのいずれかによって引き起こされる。ここで,方差によって引き起こされる関連誤差について議論する。
  
  <unk>回帰は,収縮参数λ[lambda]を使って多重共線性問題を解く.以下の式を参照.
  
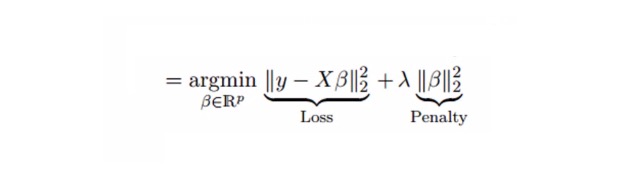
  この式には2つの構成要素がある。"つ目は最小二乗数であり,もう一つはβ2 ((β−二乗) のλ倍であり,その中のβは関連する係数である。縮小参数のために最小二乗数にそれを加え,非常に低い差分が得られる。
  
  ポイント:
  - 常数を除けば,この回帰の仮定は最小二乗回帰に似ています.
  - 関連する係数の値を縮小したが,ゼロには達していないので,特征選択機能がないことを示している.
  - これは正規化方法であり,L2正規化を使用している.
- 6. ラッソ・リグレッション
  
  <unk>回帰に似ており,Lasso (Least Absolute Shrinkage and Selection Operator) も回帰係数の絶対値の大きさを罰する.さらに,変化の程度を減らすことができ,線形回帰モデルの精度を高めることができる.以下の公式を見てください.
  
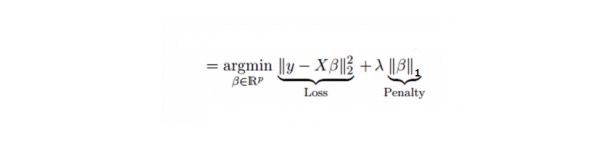
  ラッソ回帰はリッジ回帰とは少し違って,罰則関数を絶対値として使用する.これは,罰則 ((または,束縛された推定値の絶対値の和) 値がいくつかのパラメータの推定結果をゼロに等しくする.罰則値が大きいほど,さらなる推定は,縮小値がゼロに近づくようにする.これは,与えられたnつの変数の中から変数を選択する結果になる.
  
  ポイント:
  - 常数を除けば,この回帰の仮定は最小二乗回帰に似ています.
  - 収縮係数はゼロに近い ((=0),これは特性の選択に役立つ.
  - これは正規化の方法であり,L1正規化を使用しています.
  - 予測される変数の集合が高度に関連している場合,Lassoはそれらの変数のうちの1つを選び,他の変数をゼロに縮小する.
- 7. ElasticNetの帰還
  
  ElasticNetは,LassoとRidgeの回帰技術の混合である. L1を訓練するために使用し,L2を正規化マトリックスとして優先する. 関連する特性が複数あるとき,ElasticNetは便利である.Lassoはそれらのうちの1つをランダムに選択し,ElasticNetは2つを選択する.
  
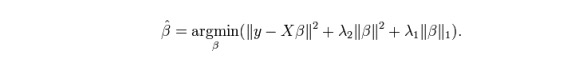
  ラッソとリッジの間の実用的な優位性は,ElasticNetがリッジのいくつかの安定性を循環状態で継承することを可能にするということです.
  
  ポイント:
  - 関連性のある変数の場合,集団的効果が生じます.
  - 選択する変数の数は制限なし.
  - 双重収縮も耐えられる
  - この7つの回帰の最も一般的な技術に加えて,ベイジアン回帰,エコロジック回帰,ロバスト回帰などの他のモデルも見ることができます.
- 逆帰モデルを正しく選択するには?
  
  1つまたは2つの技術しか知らないとき,人生は簡単である. 私が知っている1つのトレーニング機関は,その学生に,結果が連続的であれば,線形帰帰帰を使用するように教えています. 二元的であれば,論理帰帰帰を使用します. しかし,私たちの処理では,選択肢が多く,正しいものを選択するほど難しくなります. 同じような状況が帰帰帰モデルで起こっています.
  
  多種回帰モデルでは,自変数と因数変数の種類,データの次元,およびデータの他の基本的な特徴に基づいて,最も適切な技術を選択することが非常に重要です.正しい回帰モデルを選ぶための重要な要因は以下のとおりです.
  
  データ探索は予測モデルの構築の不可欠な部分である.適切なモデルを選択する際に,例えば,変数の関係と影響を識別する際に,それは第一のステップであるべきである.
  
  比較は異なるモデルの優位性に適したもので,統計学的に有意なパラメータ,R-square,Adjusted R-square,AIC,BIC,エラー項などの異なる指標パラメータを分析することができる.もう一つは,Mallows' Cp コードルである.これは,モデルを可能なすべての子モデルと比較して (またはそれらを慎重に選択して),あなたのモデルで起こり得る偏差をチェックする.
  
  交差検証は予測モデルの評価の最良の方法である.ここでは,あなたのデータセットを2つに分けます (訓練の1つと検証の1つ). 観測値と予測値の間の簡単な均等差を使用して,あなたの予測の精度を測定します.
  
  複数の混合変数のデータセットがある場合,すべての変数を同時に同じモデルに配置したくないので,自動モデル選択方法を選択すべきではありません.
  
  これはまた,あなたの目的にも依存します. 統計学的に非常に有意義なモデルよりも,より弱いモデルがより簡単に実行される場合があるかもしれません.
  
  還元正規化方法 ((Lasso,Ridge,ElasticNet) は,高次元とデータセット変数の間の複数の共線性でうまく動作する.