線形回帰 - 最小二乗法

• ### 1 序言

この間,の機械学習,第5章のLogistic回帰を学び,相当の苦労を感じました. 本の遡る源は,Logistic回帰から線性回帰,そして最小二乗法まででした. 最終的に高等数学 ((第6版;下巻) 第9章第10節最小二乗法まで格付けされ,これは最小二乗法の背後にある数学原理がどこから来たのかを理解しました. 最小二乗乗は,最適化問題における経験式を確立する方法の実現である.その原理を理解することは,Logistic帰帰帰と支持ベクトルマシンの学習を理解するのに有益である.

• ### 2 背景について

最小二乗法の出現の歴史的背景は興味深い。 (以下の文字抜粋はウィキペディア)

1801年,イタリアの天文学者ジュセッポ・ピアツィが最初の小惑星谷星を発見した.40日間の追跡観測の後,谷星が太陽の後ろに走っているため,ピアツィは谷星の位置をなくした.その後,世界中の科学者は,ピアツィの観測データを用いて谷星を探し始めたが,ほとんどの人の計算の結果に基づいて谷星を探し始めた.当時24歳のゴスも谷星の軌道を計算した.オーストリアの天文学者ハインリヒ・オルブスは,ゴスの計算した軌道を基に谷星を再発見した.

高スが最小二乗法について用いた方法は,1809年に彼の著書『天体運動論』で発表され,フランス人科学者ル・ジェンドは,1806年に独立して最小二乗法を発見したが,当時では知られていなかったため,黙って知られていなかった.両人は,最小二乗法原理を最初に創った人について論争があった.

1829年,ガースは最小二乗法の最適化効果が他の方法より強いという証明を提供した.ガース-マルコフ定理を参照.

• ### 3 知識の活用

最小二乗法の核心は,すべてのデータ偏差の平方と最小を保証することである.

戦闘船の長さと幅のデータを集めたとしましょう.

このデータから,Pythonで散点図を描きます.

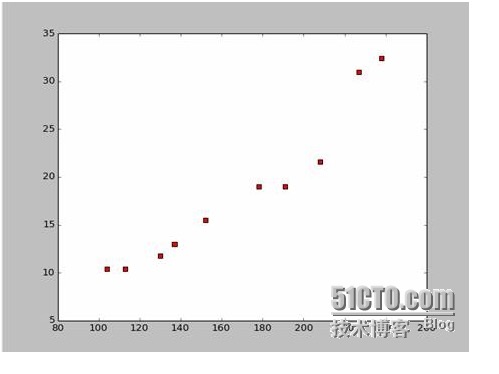
散点図のコードは以下の通りです.

  import numpy as np                # -*- coding: utf-8 -*
  import os
  import matplotlib.pyplot as plt
  def drawScatterDiagram(fileName): # 改变工作路径到数据文件存放的地方
      os.chdir("d:/workspace_ml")
      xcord=[];ycord=[]
      fr=open(fileName)
      for line in fr.readlines():
          lineArr=line.strip().split()
          xcord.append(float(lineArr[1]));ycord.append(float(lineArr[2]))
      plt.scatter(xcord,ycord,s=30,c='red',marker='s')
      plt.show()

この2つの方程式は,この2つの点から, 152*a+b=15.5 328*a+b=32.4 a=0.197,b=-14.48 となる. このグラフは,このグラフの2つを組み合わせたグラフです.

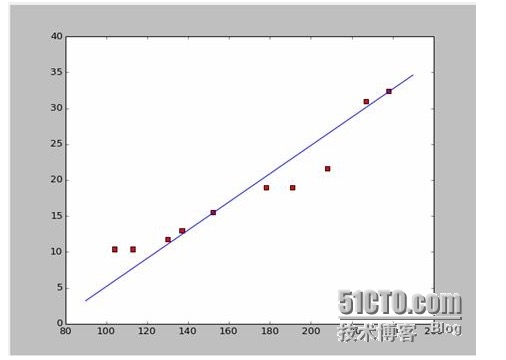
では,新しい質問がやってきます. aとbが最適解なのか? 専門用語では,aとbが最適解のパラメータなのか? この質問に答える前に,別の質問に答えましょう.

答えは,すべてのデータの偏差の平方と最小を保証するということです. 原則については,後で説明しますが,このツールをどのように使用して,最も良い a と b を計算するかについて説明します. すべてのデータの平方と最小の合計を M と仮定すると,

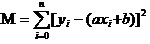
この方程式で,yとxiが既にあるので,この方程式で,yとxiが既にあるので

この方程式は,a,bを自変数,Mを因数変数とする二次関数である.

高数で1元関数の対が極値になる方法を思い出す. 導関数というツールを使っている. 二元関数では,導関数を使っている. ただ,ここで導関数には新しい名前がある. 偏導関数. 偏導関数とは,2つの変数のうちの1つを常数として導導求することである. Mの偏導関数を求めると,

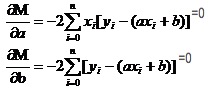
この2つの方程式では,xiとyiが既知である.

Wikipedia のデータを使っているので,直接答えを使って合致した画像を描きます.

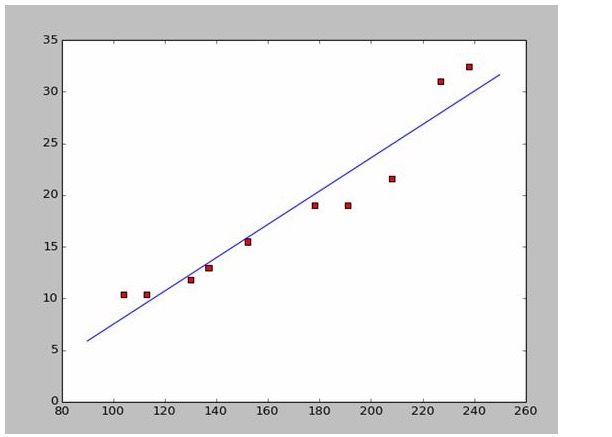
  # -*- coding: utf-8 -*importnumpy as npimportosimportmatplotlib.pyplot as pltdefdrawScatterDiagram(fileName):
  # 改变工作路径到数据文件存放的地方os.chdir("d:/workspace_ml")xcord=[];
  # ycord=[]fr=open(fileName)forline infr.readlines():lineArr=line.strip().split()xcord.append(float(lineArr[1]));
  # ycord.append(float(lineArr[2]))plt.scatter(xcord,ycord,s=30,c='red',marker='s')
  # a=0.1965;b=-14.486a=0.1612;b=-8.6394x=np.arange(90.0,250.0,0.1)y=a*x+bplt.plot(x,y)plt.show()
  # -*- coding: utf-8 -*
  import numpy as np
  import os
  import matplotlib.pyplot as plt
  def drawScatterDiagram(fileName):
      #改变工作路径到数据文件存放的地方
      os.chdir("d:/workspace_ml")
      xcord=[];ycord=[]
      fr=open(fileName)
      for line in fr.readlines():
          lineArr=line.strip().split()
          xcord.append(float(lineArr[1]));ycord.append(float(lineArr[2]))
      plt.scatter(xcord,ycord,s=30,c='red',marker='s')
      #a=0.1965;b=-14.486
      a=0.1612;b=-8.6394
      x=np.arange(90.0,250.0,0.1)
      y=a*x+b
      plt.plot(x,y)
      plt.show()

• ### 4 原則 探求

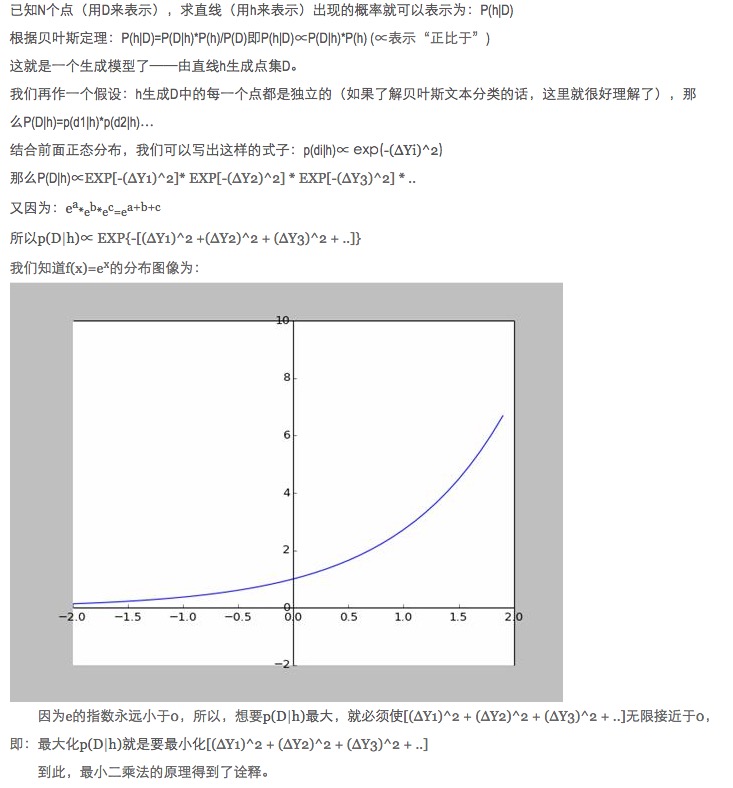
データマッチングでは,なぜモデルのパラメータを最適化するために,絶対値と最小値ではなく,モデルの予測データと実際のデータとの二乗の差を用いなければならないのか?

この質問には既に答えが載っています (リンクをご覧ください)

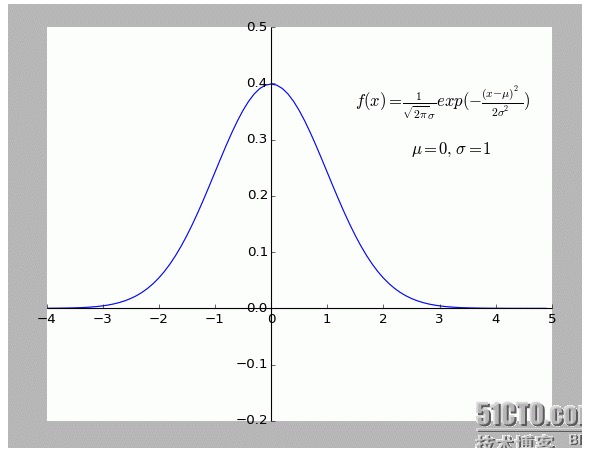
個人的にはこの説明がとても面白いと思います.特に,その中の仮定は,すべての偏り f ((x)) の点は騒々しいということです.

一点偏離が遠くなるほど,騒音が大きくなると,その点が発生する確率は小さくなります. では,偏離度xが発生確率f ((x)) とどのような関係にあるのでしょうか? 正規分布です.

• ### 5つ目 拡張

上述の状況は二次的であり,すなわち自変数一つしか存在しない。しかし,現実世界では,最終結果に影響を与えるのは,複数の要因の重複であり,すなわち自変数がある状況である。

一般のN元線形関数については,線形代数の逆行列で解き明かすことはOKである.暫く適切な例が見つからなかったので,引数としてここに置く.

自然界は,単純に線形ではなく,多項的適合であり,それこそより高度な内容である.

• 参考文献

  • 高等数学 (第6版) (高等教育出版社)
  • 線形代数 (北京大学出版社)
  • インタラクティブな百科事典:これは,最小二乗です.
  • ウィキペディア:最小二乗法
  • サイエンスネット:“最小二乗”は,神馬にとって悪い絶対値ではありません.

原作,転載許可,転載の際には必ず超リンク形式で記事のオリジナル・ソース,著者情報,本声明を記載してください。そうでない場合は法律上の責任を負います。http://sbp810050504.blog.51cto.com/2799422/1269572