ギャンブルと投資における「脱出」と「生き残り」の物語

---

ギャンブルや投資について言えば,人は通常,お金を稼ぐ術を学ぶために急いでいます.実際,私はお金を稼ぐことは,学ぶのは簡単ではありません,経験と悟りが必要です. 段落を迅速に向上させたい初心者は,まず防御をよく練習する必要があります. 防御は,学習可能な特定の方法を持っています.
逃亡<unk>のシリーズを作ろうとするのは,小学生に逃亡<unk>を教えることではなく,仲間や仲間と逃亡<unk>の学問を考察することだ.
3年前,<unk>証券紅週刊の<unk>とのインタビューからインスピレーションを得ました. 記者の誘導を受けて,私は投資取引のビジネスに関する深い洞察を述べ,世界経済金融状況に関する宏説を発表した.

• ウォール街のトップ操縦士のフィッシュ・ヤンの<unk>が逃亡の秘密

  悲しいかな.

  インタビューではリスク管理の重要性について話し,自分の取引で成功したいくつかの突発的な例を挙げているだけで,どうして<unk>逃命<unk>になったのか?しかし,注意深く考えてみると,ジャーナリストの編集者の鋭敏さを称賛しなければならなかった.アメリカの投資は,中国人の一般市民と少し遠く,大局の宏論は,私の記事より,<unk>逃命<unk>は比較的空白の話題である.これは少し奇妙に聞こえるが,長期的な投資の成功にとって不可欠である.石田は大河を渡り,四渡り会長が赤水奇兵を渡り,勝利と敗北の境界の差は,<unk>逃命<unk>の文字にしかならない.

  <unk>心武先生は,<unk>可卿の謎から始まり,福ルマスの道を踏んで<unk>学術<unk>を仕上げることができ,<unk>は,<unk>逃命<unk>から始まり,<unk>逃学<unk>を発展させることができると言った.<unk>紅週刊<unk>の千語以上のインタビューが始まり,今,私たちは話を進めます.

  遠方からお見舞い申し上げます 遠方からお見舞い申し上げます

  最近,多くの読者がウォール街の乱世について最も興味を持っているのは,ギャンブルに関する冒頭部分である ((以前,ロンドンのトレーダーが郵便受けの友人に電子版を送信し,みんなに役立つことを望んでいた).21点は,利率の落ちる期よりも大衆に近いようです.

  • 生きていることが一番です

    ギャンブルや投資について言えば,人は通常,お金を稼ぐ術を学ぶために急いでいます.実際,私は個人的に,お金を稼ぐ方法は,学ぶのは簡単ではありません.多くの経験と悟りが必要です.初心者は,ギャンブル段落を迅速に向上させたいので,まず防御を練習すべきです.防御は,学習可能な特定の方法があります.私の考えでは,ギャンブルや投資の成功の前提条件は,防御をよくして,資金を貯めて,そして忍耐して本当の機会を待つことです.

    革命が勝利するまでは,絶対に犠牲にならなかれ. 簡単にできるとは思わないで, 投資界のトップにいる人でも, 雲から落ちた人がたくさんいることを言うまでもなく, 周りには,金持ちになりながら, 命を落とそうとする仲間や仲間がいる.

    この記事では,

    ジェシー・リヴァーモア: <unk>株の作家の回顧録<unk>の主人公,投機界の天才は,無作で家から1929年に1億ドルの資産まで成長し,最終的に破産を申請し,数年後自殺した.

    ジョン・メリーウィーサー:かつて,スロモンズ・ブラザーズのスーパートレーダーで,その後,星<unk>の長期資本ヘッジファンド (LTCM) を設立し,かつて400億ドルの巨額の資本を持っていたが,1998年のロシア債券危機でほとんど損なわれた.

    管金生:1988年に万国証券を設立し,中国証券の父として知られていたが,1995年に3.27国債事件で中馬が失格し,罠に陥った.

    唐万新 (唐万新) 氏:以前はドロン系企業グループを統括していたが,中国資本市場を傲慢に扱った結果,資金連鎖が破裂し,ドロン帝国が崩壊した.

    資本市場における天才であるこれらの人々は,結局は失敗した.彼らの経験は,リスクの管理に注意を払わずに,<unk>漁師と金魚の<unk>のシーンが起こることを教えてくれます.努力して教皇に選ばれたが,結局は海辺の小屋に戻りました.

    生きていることが一番です.

  • わからない,わからない.

    何年も前,私はニューヨークのチャイナシティから大富豪のバスに乗って大西洋<unk>城へ行き,乗っていたのはレストランの廊下で働く労働者でした. 彼らは,カジノで運命を変えようとしたが,結果として,しばしばわずかな給料を支払いました. 隣の女の子が,毎週カジノで百ドルをプレイし,秘訣を勝ち取るという話をしたのを覚えています.

    帰り道で,私は800ドルを勝ち,彼女は4000ドルを落とした.私は突然興奮し,4000ドルは彼女の1ヶ月以上の収入であるべきだった! シンプルな同胞の衣装で満載した車を見て,私は突然悲しく感じ,大金を稼ぐ大バスビジネスをやっている人たちを憎む,それは虎の口に羊を送るようなものだ! 私は女の子に百貨店で長らく勝つことを伝えようとしたが,彼女は信じようとせず,この勝利は運が悪かっただけで,来週また本を見直すと言った.

    失敗した人は 幸運を言い訳にして 失敗を言い訳にしています

    一回負けたら勝ち,万回負けたら勝ちというのは大数理だ (勝率が高い人はほぼ必ず勝つ).賭場での賭けの確率優位なゲームで,負けたら負けることは時間の問題ではないだろうか.だから,賭場はあなたが勝つことを怖がらず,あなたが来ないことを怖がっている.

    投資も同様です

    株式市場はカジノより優れているので,長期的には正利益のゲームであるはずである。しかし,賭博,内幕取引,印税などの要因のために,普通投資家は,賭博が頻繁であれば,利益率は大市で勝つことは難しい,あるいは,長生きしても必ず負けるかもしれない。だから,市場で,早速金持ちになるという秘訣を教えてくれる人たちを信じてはならない,99%は浮き雲であり,99%は怠惰である。最も重要な招きは,どうやって招き出すかではない。

    江戸時代,日本に<unk>剣聖<unk>宮本武藏がいた.彼は60回以上の人とデュエルを戦ったが,決して敗れなかった.彼は技巧の卓越に加えて,秘訣がある:決して自分よりも強い人と戦わない.

    村の村長が,村の村長に,村の村長に,村の村長に

    これはハッカーも投資家も覚えておくべき第一の秘訣です.

    

  • カジノの利点は?

    カジノはあなたが勝つことを怖がらず,あなたが来ないことを怖がる,なぜなら,カジノゲームは,基本的に,長引くことで必ず負けるものだ.多くのプレーヤーは,幸運に迷信し,カジノを運営する人は,確率を信じている,それが敗者と勝者の違いだ.

    例えば,輪盤<unk> (下図を参照),賭博では,プレイヤーは任意の数字に賭けることができる.もし,回転盤上の小さなボールが,この数字に正常に止まれば,賭場は35倍に賭ける.

    魅力的な音ですよね?

    映画『カサブランカ』の少年がヨーロッパから逃げた後,22人の囚人が拘束され,アメリカへの旅費が支払われた.

    簡単な分析をしてみましょう.

    

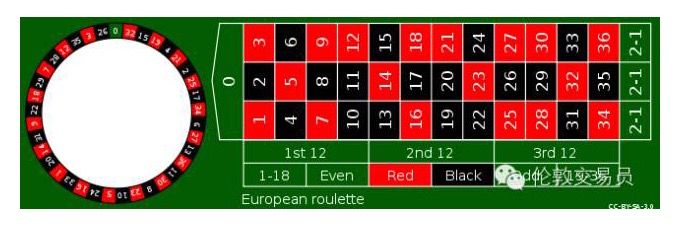
    この36つの数字が1-36しかなかった場合,プレイヤーは1ドルを1回賭け,平均36回勝1回,勝った35ドルは,もう35回の負けた金を正常に抵消する.しかし,カジノは輪盤の左側に0円を足し,プレイヤーの勝面は1/37になり,勝った35ドルは,もう36回の負けた金を抵消するには不十分で,カジノは1/37=2.70%の確率優位を占める.つまり,プレイヤーは100ドルを賭け,平均2.7ドルを負ける.また,これは<unk>仁慈のヨーロッパ輪盤であり,アメリカ人はまだ黒が足りないと感じ,さらに00円を追加した (下図参照).現在,平均38回の賭けで,プレイヤーの劣勢は5.3%に拡大している.

    

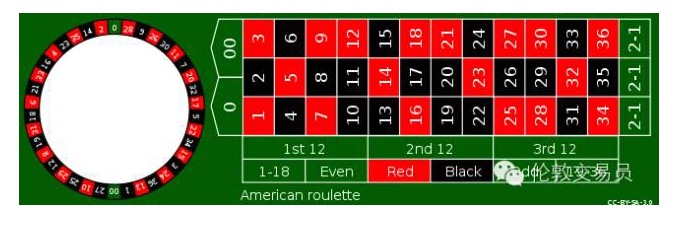
    単数賭けに加えて,輪盤<unk>には,赤黒などの賭けがあります. 1対35の単数,または1対1の赤黒の賭けでも,カジノの勝面は同じです. しかし,両者の間には重要な違いがあります. 単数賭けの負勝波動は,赤黒賭けよりも明らかに大きい.

    ギャンブルと投資の2つのポイントは,勝率と波動性です.

    <unk>久<unk>必勝の賭博は触らないほうがよい.実際に遊ぶには,負け勝ちの変動が大きいことを挑み,<unk>久<unk>必勝の投資は,変動が小さいものを選ぶべきである.この原理については,後述で詳しく議論する.

    ギャンブルに戻ると,ほとんどのカジノゲームは,ロッカーのように設計されています.カジノは確率の優位性を持っています.これらのゲームでは,プレーヤーは,数回しかプレーしない場合でも,幸運に賭けてお金を稼ぐことができます.長期間プレーすると,ほぼ必ず負ける.数学では,大数の法則と呼ばれています.

    しかし,カジノの機械は,数学者によって破綻した.

  • 21時の古い物語

    1960年代初頭,エドワード・ソープというアメリカの数学者は,新興したコンピュータを使って21点のゲームのチャンスを見つけ,カードカウント (card counting) を使ってカジノを倒す方法を開発した.ソープ教授は理論を実践し,自分のカードカウント法でカジノを連勝し,すぐにブラックリストに載せられ,目に見えないことになったので,誰かが本を書いた!

    ソープの『ビート・ザ・ディーラー』が70万冊売れ,ニューヨーク・タイムズ・ベストセラーリストにランクインした. 『ウォール街のギャンブルを連想して,著者は恥じています. . .』の版税収入は,ギャンブル収入をはるかに上回っています.

    ソープカード計算の原理は難しいではない。まず21点のルールについて語ろう:プレイヤーと庄家 ((カジノ) が対戦し,誰の手のカードのポイントの合計がより近い ((しかし,それ以上にはならない) 21点を見る。10,J,Q,Kは10点であり,2から9までの各ポイントの計算により,Aは1点でも11点でもよい。例えば,下記の手のカードは8点でも18点でもよい。

    

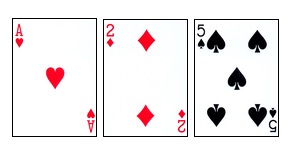
    カード局は,プレイヤーと庄屋がそれぞれ2枚のカードを振って,庄屋のカードが明暗である (下図のように).その後,プレイヤーは最初に決定します:カードをクレープし,ダブルするなど特別な動作を行うか,またはいつでも休止を選択してください.プレイヤーが21点を超えた場合 (爆破カード) は直接負ける.そうでなければ,休止は,休止の後,庄屋の動きに変わります.庄屋は機場行列を見ることができないが,固定ルールに従ってしか行けません.手の中のカードが17点に達した場合,休止をしなければならない.

    

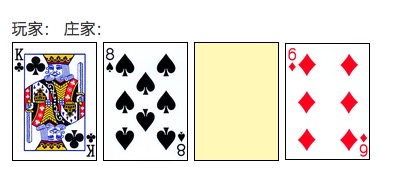
    また,特殊な規定があります:Aと10点のカード ((10,J,Q,K) をブラックジャックと呼んでおり,それを手にすると直接勝利します. プレイヤーがブラックジャックを手にすると,1.5倍のチップを獲得できます. 庄屋がブラックジャックを手にすると,1倍のチップのみを獲得できます.

    21点のゲームでは,庄家とプレイヤーがそれぞれ優位であることは明らかである.庄主の優位は,<unk>の後の人気制覇である:プレイヤーが最初にカードを爆破すれば,庄主は勝てることなく勝つことができる.そして,プレイヤーの優位は,柔軟な動きであり,自分のカードと庄主の開いたカードに基づいて戦術を決定することができる.さらに,ブラックジャック3:2の確率もプレイヤーに有利である.

    10点カードやAが多くなるほど,ブラックジャックのチャンスが多くなるが,爆破のチャンスも多くなるが,プレイヤーの<unk>動的な柔軟な<unk>の優勢はより価値ある.逆に,3,4,5,6などの小カードが多くなるほど,爆破のチャンスが少なくなり,庄家にとって有利である.

    ソープ時代の21は1副または2副のポーカーカードを使用し,カードが洗浄されたとき,カジノは約0.5%の確率優位を占めています. 奇妙なことに,カード局が行われると,時には大牌とAの比率が高くなり,確率はプレイヤーに有利に転じます.ソープのカジノの勝利方法は,カードの確率を推定して,状況が有利であるときに大きな賭けをすることです!

    ソープはカードを計算し,ベストセラーを書き,ウォール街で大金持ちになり,ヘッジファンドで大金持ちになった.

    カジノ側では,ソ氏武功を掌握した<unk>計カード客<unk> (card counters) が現れてきた. カジノ側では,カード客<unk>を門外へ退けようとし,カード客<unk>は空洞を掘り出し,ブロックを突破しようとした. 猫とネズミのゲームは数十年続いたが,90年代前後,江湖でまた不思議なことが起こった.

    物語は,結局,投資に還元されます.

  • MITのカードゲーム

    ソープの話をすると,カジノはカードカウンターを捕まえるトラブルに巻き込まれました. 長いこと,カジノはブラックリストを積み重ねてきました. リストに載っている人が21点のカードテーブルで認識されれば,通常はすぐに国外送還されます.

    1980年代のある時期に,カードカウンター詐欺事件が急増し,カジノで雇われた探偵は,各所で収集されたブラックリストを研究し,重要な手がかりを発見しました:多くのカードカウンターの住所は,マサチューセッツ州ケンブリッジ市周辺にあります! マサチューセッツ州ケンブリッジ あなたは聞いたことがないかもしれません,しかし,この地域の2つの大学 (ハーバード,マサチューセッツ工科大学) は聞いたことがありません.

    そして,その真相が明らかになり,MITの学生たちが主役のトランプゲームが登場しました.

    これは,<unk>商化<unk>で運営される組織である.誰かが<unk>を出す,誰かが管理する,誰かがプレーを計算する,全体の<unk>投資<unk>と<unk>リスクコントロール<unk>のモデルには,ヘッジファンドの風俗がある. 集団<unk>の最大の利点は,単一の<unk>客が直面するリスクを回避できるということだ:21点の勝ち負けの変動性が大きい,あなたが技術的に優れているほど,短期間の運が悪いとしても,<unk>を落とす可能性がある. 集団作戦は,このリスクを分散させる. さらに,MITの<unk>客は,いくつかの<unk>多人戦術も使用している.

    例えば,マイケルはカードを数え,小さな賭けごとに,状況が有利なときに,前もって決められた暗号を投げます.このとき,少佐のジェームズがやってきて,1000ドルを賭けます.

    MITのグループは十数年間,MITやハーバードなどの学校が参加し,オリンピックの金メダルを獲得した中国人もいました. 鉄打の兵隊は水を流し,とにかく,マサチューセッツのケンブリッジ地区には数学天才が欠かせません. このグループの収益は,数百万ドルで,後に,MITのグループの功績に油を注ぎ込んだ作家が本に書き,ニューヨークタイムズのベストセラーリストにも載りました.

    1990年代中頃,アメリカの経済が好転し,ギャングはシリコンバレーやウォール街などに移動し,MITのギャングは徐々に散らばった.これは,若者が正規の仕事をすることで,犯罪率が低下するという事実も証明しているように思われる.

    それから数年後,中国から来た漁陽の同級生が偶然21点の計札に触れたので,とても興味が湧きました。当時はソップのことを聞いたこともなく,ソップ宗師の本が"冊で10ドルしか売れなかったことを知らなかったので,カドサという大人の無駄遣い者から100ドルかけて,いわゆる<unk>の秘書を買いました。高価格の<unk>で刺されても,結局は<unk>があるので,私もカジノで金を掘り!

    江湖は,その年の江湖ではなくなった.

  • ギャンブルに関する混乱

    カードを計算する方法を学んだ後,私は興奮してラスベガスへ行った. 結果は,とても良かった. 100ドルの大金を勝ち取った. これは21点,本当に金鉱だ! 私はニューヨークに住んでいて,いつもラスベガスへ行って金鉱を掘るわけにはいきません. ニューヨークの近くには,アメリカ第2位の大金鉱の都市であるアトランティックシティもありますので,私はそこで常客になりました.

    大西洋シティの金砂場は,好ましくないと気づきました. 大西洋シティは,大西洋シティとラスベガスとは違うと気づきました. 大西洋シティの金砂場は,大西洋シティとラスベガスとは違うと気づきました.

    前述の通り,カードカウンターは主に大小のカードが残ったカードの割合を見て,大牌の割合が普通より高いときは大賭けをする.

    明らかに,比率は2つの状況で最も高くなるのが容易である.一つ目は,残ったカードが少ないときであり,二つ目は,21点のゲームが1-2副カードしか使わないときである.ソップ時代の21点の賭け場は,まさにこの2つの特性を有している.1-2副カードのみを使用し,カードの配達者 (ディーラー) はほとんど光でカードを洗うだけなので,大きなカードの比率は常に高くなり,カードのカウンターは,状況が有利なときに大きな賭けをする機会がたくさんある.

    カジノでは自然にも高官の策略がある.計測カードの最も良い軟防線は,大小カードの比率の変動を制御するものであることを理解している.そのため,カジノは2つの毒計を作り出しました.第一は21ポイントの使用カードを追加し,1-2副から6-8副に普遍的に変更しました.

    明らかに,カードが多く,大きさと小さいカードの比率は変化しない.

    2つ目は,早期に洗牌し,比率が最も変動しやすい状況を避けることです.ラスベガスカジノは多々で,競争は激しく,カジノはギャンブル客のために1-2副カードの21点のゲームを保留しているので,私は主にそれらのギャンブルでお金を獲得しました.そして,大西洋街の地理的位置は,ニューヨーク,ワシントン,フィラデルフィアの3つの人口密集した地区のギャンブル客がそこに走るので,カジノはビジネスに悩まされませんでした.したがって,21点のゲームの規則は特に黒いです:基本的には8副カードであり,洗浄は勤勉です.大小の割合が高くなる頻度は低いので,自然にもお金を獲得することはできません.

    江湖は,ソップの江湖ではなくなった.

    しかし,比例は高くなっていても,カジノには勝面がある.前述の<unk>大数法則<unk>:勝面がある限り,理論的にはずっとプレイして最後は私が勝つ.しかし,理論は理論に帰る,実践には重要な制約がある.私の賭けは限られている,負けたら遊ぶことはできません.<unk>大数法則は,<unk>革命が最終的に勝利すると言うだけで,<unk>革命の勝利前に<unk>を犠牲にしないことを保証しません.21点の負けた勝利の波動性は非常に大きいので,ブラック・スワン ((Black Swan,微小確率の小事件) を追いかけるならば,<unk>の栄誉は得られないのですか?

    賭け場が"%の確率で勝てるまで待つのは簡単なことではありません.

    <unk> Place your bets. <unk> (あなたの賭けをしてください)

    平均で2セントしか稼げないけど 2,000ドル賭けたら?

    20ドルは少ないし,2000ドルは多いし,最高の賭けはどちらかです.何に賭けるべきでしょうか?

    答えを教えてくれたのは高官だ

    投資の理論について語ろうと思います.

  • ケリー公式

    前回言ったように,状況が有利なときにどのように賭けるかには技が必要である。賭けすぎると無駄なチャンスが少なく,賭けすぎると<unk>を犠牲にするリスクが大きく増加する。何が適当な賭けなのか? 1956年,科学者ケリー (John Kelly) は,このことについて論文を発表し,有名なケリー公式を提唱した。

    f* = (bp - q) / b
    f* = 投資額が総資本に占める割合
    p = 勝つ確率
    失敗する確率は,q=1-pです.
    b = 確率,例えば,輪盤の1つの数字に賭け,b = 35,赤黒に賭け,b = 1。

    前記事で述べた21点の賭け問題では,総賭けが10,000ドルと仮定し,プレーヤーの勝利の確率は51%で,1:1の確率で (実際の勝利率と損失率はわずかに偏っているが,大きな差は無い),ケリー公式で与えられた最良の賭けは次のとおりである.

    $10000 * (1 * 0.51 - 0.49)/ 1 = $200
    数学の公式を見て頭が大きくなるのはよくあることですが,賭博や投資をするには数学を使わなければいけません. 重要なのは,公式を使って数字を計算することではなく,公式の背後にある本当の意味を理解することです.

    まず,bp - qの分子式は,<unk>の勝面<unk>を代表し,数学では<unk>の期待値<unk> ((expectation)) と呼ばれる.ケリー公式は,正の期待値のゲームのみを賭けることができる,これはすべての戯れや投資の最も基本的な理念である,すなわち,前述の<unk>は把握がない,決して<unk>を賭けない.

    2つ目は,勝面を<unk>b<unk>で割るのみが投資資金の比率である.つまり,勝面が同じである場合,確率が小さいほど,より多く賭けることができる.この点は直観的に理解するのは容易ではないので,例で説明する.以下の3つの正の期待値のゲームで,どれを選ぶか見てみましょう:

    <unk>小博大<unk>:勝率20%,勝1負5敗全光。bp - q = 520% - 80% = 20%
    勝率60%,1対1 △bp - q = 160% - 40% = 20%
    <unk>大博小<unk>:勝率80%,1負け0.5。bp - q = 0.5*80% - 20% = 20%

    3つのゲームの数学的な期待値と同じで,20%,つまり100ドルの賭けで平均で20ドルを勝ちます。ほとんどの国の人の<unk>性によって,大賭けのゲームを選ぶでしょうね? しかし,ケリー公式の<unk>bを分割すると,大賭けのゲームは総資金の4%しか賭けられないし,中賭けのゲームは20%,大賭けのゲームは40%しか賭けられないのです。お金の獲得速度は大賭けのゲームより速いです!前述は<unk>久<unk>の必勝ゲームが変動のゲームを選ぶべきではないですか? 言うまでもありません。

    ギャンブルを好きな人の多くは,実際にギャンブルをやっている人達です.

    ギャンブルを好きな人はいるか?

    ウォール街のプロの投資家は,レバレッジを利用して『大賭け』をするため,大賭けも多くしている.

    最後に,ケリー公式は,リスク管理が不可欠であることを示しています. 正の期待値のゲームでも,大きな賭けはできません. 数学的に言えば,賭け金比率はケリー値を上回り,長期にわたる金儲けの速度は逆に低下し,破滅的な損失の発生の可能性も大きく増加します. 極端な例を挙げると,もしあなたがすべての手を賭けると,あなたがどれだけ稼いだとしても,一度だけ負けたら,すぐに破産します.

    なぜ投資界は,一部の技術的に優れた老人に財産を落としてしまうのか? その理由は,大抵は賭けすぎているからです. 20世紀初頭,大師級の投機家の英一世は,このことで名声を落としたのです.

    リヴァモールはメイスティンを倒した.

    

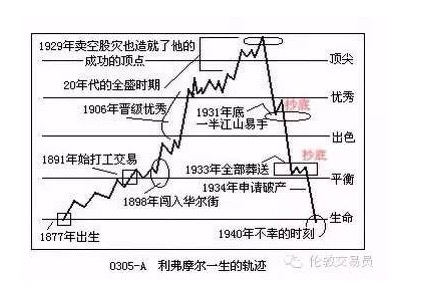
    ケリー公式の誕生から16年前の1940年11月28日,ニューヨークのウォルドルフ・ホテルのロッカールームで,ウォールストリートの独り歩きだった男が銃を抜き,妻に手紙を残した. "<unk>...私は戦いにうんざりした...これが唯一の解放だ.<unk>,そして弾丸を飲み尽くせ".

    ジェシー・リヴァーモア (Jesse Livermore) は,不朽の名作『<unk>株手伝』の主人公で,こうして伝説的な人生を悲しみに終えた.

    もし,あなたがまだ『株式オペレーターの追憶』を読んだことがないなら,このレッスンを補うことを強くお勧めします.世界一流のヘッジファンドマネジャーは,この本を非常に高く評価しています.主人公の人生の起伏を追うと,百年以上前に乱れながらも活気のあるアメリカの金融市場の様子を感じることができ,世界がフォーモールのような才能に恵まれていることに驚きます.

    彼は原始的な時代を<unk>いでいて,多くの現代投資家の古典的な法則をまとめました. 例えば,儲けるときは加えて,損をする時は止めて,他人の意見を軽視してはいけない,あるいは,<unk>の内部情報<unk>,そして<unk>の座席<unk>の完全な手法.

    さらに驚くべきことに,リヴァーモールは理論家だけでなく実践者でもあった.彼の取引は,何百万ドルの価値から,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万ドルの価値まで,何百万もの価値まで,何百万もの価値まで,何百万もの価値まで,

    文献には詳細な記録はありませんが,彼の取引習慣を注意深く分析すると,ヒントを見つけることが容易になります.

    リヴァモールの取引キャリアはBucket Shop (バケットショップ) から始まった.

    19世紀末,アメリカの株式市場は活気があり,技術の進歩により,ニューヨークから遠く離れた普通の人も,リアルタイムで株式投機に参加する機会を得ました.電報線に接続された自動報付マシンは,ニューヨーク取引所の最新の取引価格をいつでも全国中に伝わることができます.当時,投機に参加したい人が多かったが,株式を購入したり販売したりするための資金が不足していたので,詐欺師は,この機会を利用して,これらの人々を<unk>の株式カジノに誘いました.

    カジノにはオートバイがあり,プレイヤーは実際に<unk>の大きさで株式を取引しているように見えます.例えば,ある株式の最新オファーは80ドルで,プレイヤーは1ドルの保証金だけで<unk>大<unk>を購入することができます.オファーは79ドルまたはそれ以下で表示されれば,申し訳ありません.オファーは81ドルで表示されれば,プレイヤーは1ドルの利益を現金化することができます.

  • 株式会社カジノの売春婦たちはどうやって稼いでいるの?

    大衆がよく間違いを賭ける特性を利用することに加えて,彼らはいくつかの証券商による市場操作の陰謀を企んでいる.例えば,80ドルの価格で多くのプレーヤーは大金を賭けた.カジノの庄家たちは,ニューヨーク取引所の仲間が株価を圧迫するように指示し,自動価格表で79ドルの価格を打つだけで,カジノは大金を賭けたチップを食い尽くした.

    当時まだ若いリヴァーモールはお金がほとんどなく,株式賭場で混じり,徐々にオファーを基に市場価格を予測する (Read Tape) の技を習得した.当時,コンピュータもリアルタイムK線図もなかった,リヴァーモールの<unk>読盤<unk>功は,実際に技術分析の原型であった.

    しかし,彼は株式賭博で,大きな賭けをするという悪癖を身につけていたのではないかと疑っています.

    ケリー公式の観点から分析すると,株式カジノの超低担保金は実際には賭け家の<unk>殺<unk>である.利差が大きいほど,賭けははるかにケリーを上回る最高の価値であり,損失は遅かれ早かれである.当時のアメリカの正規の金融市場での取引担保も低かった.リヴァーモールの後の取引経験は,彼が常に超大賭けのスタイルを維持していることを示している.

    株式,綿,大豆,何であれ,超高レバレッジの全仓操作,これは確かにリヴァーモールの伝説的な偉業を達成し,彼も数回破産させた.幸運にもいくつかの貴族の助けがあったので,リヴァーモールは1907年,1915年,1929年にいくつかの重要なチャンスを掴み,ピークに達することができました.

    利物浦は100万ドルを手に入れた数年後,全財産を失ってしまったのは,賭けすぎのせいだと私は疑っています.

    リーバモアがケリー公式に基づいた資金管理方法と,彼の超高水準の市場把握力を組み合わせると,この天才はどんな奇跡を成し遂げられるでしょうか?

    歴史には"もし"がない.

    リーヴァモールは流星のように飛んでおり,おそらく数十年前に生まれているだろう.

    資金管理とリスク管理の理論は50年代から形成され始めた.

    ケリー公式は,大きな勝面と小さな波動のゲームで,大きな賭けができます. では,大きな勝面と小さな波動の賭けをどのように量化するか? ケリーと同時代の一人の学者によって,有名な指標が提出されました.

  • シャープ比率

    投資機会の優劣は,期待される収益とリスクの両方から総合的に考慮されるべきである.この考えはどのように量化されるのか? 1950年代に,期待される報酬と変動性の比率を投資機会の測定指標として使用することを提案した. 1966年に,学者シャープ (William Sharpe) は,この基礎で有名なシャープ比率を提唱した.

    S = (R <unk> r) / σ,その中:
    R = 投資に対する期待される収益 (平均収益率)
    r = リスクのない投資のリターン ((投資国債のリターンとして理解できる)
    σ = 還元率の標準差 (変動性を測定する最も一般的な統計指標)

    シャープ比Sが高くなるほど,投資機会の質が高くなる.

    A投資: 超額 (国債を上回る) 利回りは10%,標準差は20%,シャープ比率は0.5
    投資B:超リターン期待5%,標準差5%,シャープ比率1

    一見すると,A投資のリターン期待が高く,比較して良いチャンスのように見える.実際,B投資は,シャープ比率が高く,投資家が1ユニットの<unk>のリスク<unk>と交換してより多くのリターン期待を意味している.また,レバレッジ投資の観点から同じ結論が得られます.投資家がr貸金利率で資金調達し,B投資の機会に1倍のレバレッジを加えたと仮定すると,レバレッジ化<unk>のB投資は,10%のリターン期待,10%の標準差,A投資のリターン期待と同じで,リスクはより小さいになります.

  • シャープ比率はどのくらいの割合で 優秀な人になるのでしょうか?

    実例を挙げると,アメリカの株式市場の長期年平均リターンは約10%,波動性は約16%,無リスク利率は約3.5%,そのためシャープ比率は約0.4である (引用元:Wikipedia).

    長期投資の小売業者の場合,米株のリスク/リターンは過去のことである.ヘッジファンドのマネージャーの場合,このようなシャープ比率はあまりにも低い:あなたが年間20%のリターンを目標とすると仮定すると,2.5倍以上のレバレッジが必要である.10% - 1.53.5% ≈ 20%),つまり平均6年中1年分の収益率は2.5以下になる.（10% - 16%）- 1.53.5% = -20% 負けたら20%以上で 顧客は逃げてしまいます

    一般的に言えば,シャープ比率が1を超えれば良いゲーム<unk>である。この機会は,シンプルな投資<unk>ではあまり見られない.そのため,プロの投資家は,しばしば,ヘッジ手段を利用して,ヘッジ投資ゲームの改造をしてシャープ比率を向上させる。乱世ウォールストリート<unk>では,ヘッジとレバレッジは双生児の姉妹であり,両者はしばしば配合して使用され,この原理である。

    例えば,もしあなたが様々な資産を相互に隠蔽して,シャープ比率2の投資機会を手に入れる方法を考案したら,あなたは大胆に利子を加えることができます (数学に精通した同級生は,自分のお金を失う確率を自分で計算できます) 投資家はおそらくあなたのヘッジファンドに投資するでしょう.

    しかし,ヘッジ+レバレッジの投資方法には,多くの場合,問題がある:多くのお金を借りる必要があり,流動性の要求が高く,突然の危機に遭遇することがよくあります. ウォール街の混乱の中で,LTCMと高盛のグローバルアルファファ基金の例を分析しました.

    シャープ比率にも欠陥がある.それは,リターンが正規分布であると仮定し,実際の投資リターン分布は<unk>肥尾がある (正規分布の推定よりも大金を失う確率は高い) のため,単にシャープ比率に基づいて投資機会を選択する問題があり,<unk>操作にも容易である.このトピックは,ここでは議論されない.

    一般的な投資家の場合,シャープ比率はリスクとリターンの観点から総合的に考え,高い価格よりも高い価格の投資を選択することを示唆しています.これは,前回の記事で言及された考えです.

    シャープ比は,ゲーム上の<unk>の選び方について, ケリー公式は,ゲーム後に,どのように賭けても,長期的に見れば,最高の報酬率を得られるかについてです.

    シャープ比に関する補足

    シャープ比率に関して,問題点は以下のような部分に集中しています.

    最初の質問:アメリカの株式市場の例では, 平均6年分の1年のリターンが -6%未満である場合, どのように計算されますか?

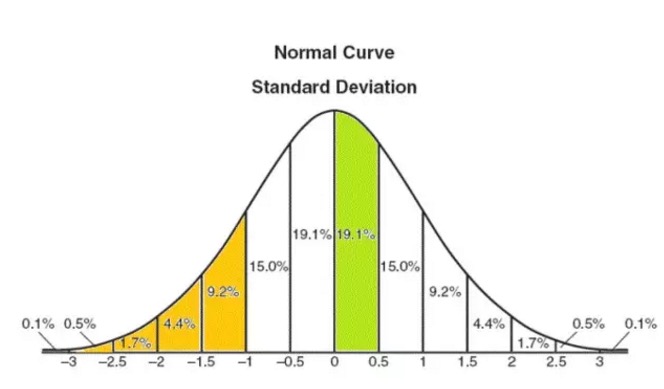
    シャープ比率は,投資収益が正規分布に適合することを仮定する (下図を参照).数学的に言えば,多数の独立したランダムな出来事の和は,一般に正規分布に適合する.例えば,硬貨を絶えず投げ,正面は1,反面は-1,大量に繰り返す結果の和は正規分布に適合する.前回のブログでは,学術界で流行っている有効市場理論の<unk>について言及した.株式市場の動きの方向の各ステップは,独立したランダムであり,硬貨の<unk>を投げ続けることと同等であり,最終的に収益率は,当然正規分布に適合する.次に,数量金融の基礎授業の<unk>のランダムなプロセスについて述べる.それについて賭けます.

    正規分布の仮定は不完全であるが,理解の問題の基本的枠組みである.下図は正規分布の確率値を示している.例えば,報酬率は0倍から0.5倍標準差の間の確率は19.1%である (図の緑の部分).

    同様に,リターン率が標準差の1倍以下 (図の<unk>色部分) の確率は約16%である.これは米国株式市場に適用される (平均リターン率は10%,標準差は16%),年間リターン率が標準差の1倍以下である可能性は約1/6である.つまり10%-16% = -6%である.平均6年のうち1年のリターン率は -6%以下である.これが,<unk>の推定である.

    シャープ比率の仮説は現実と矛盾しているのでしょうか?

    もちろんあります。正規分布の仮定は完璧ではありません。 実際には,株式市場の動きは完全に独立してランダムに<unk>を走るわけではありません.そうでなければ,我々は何の法則も研究する必要はありません。 例えば,金融危機において,株式市場の動きには非常に強い連続的関連性 (serial correlation) があり,すなわち<unk>の傾向<unk>,結果として実際の株式市場の返還には<unk>の肥尾<unk>現象が起きます.つまり,<unk>が極端位置に<unk>を走る確率は正規分布の推定よりも高い。

    また,シャープ比率の無リスクリターン比率rは曖昧な概念であり,投資家の資金調達コストもrではない.また,波動性の計算も簡単な問題ではない.他の多くの論文では,シャープ比率の限界と改善案について議論されている.

    シャープ比率は一般投資家にどう役立つのか?

    投資は利回りだけではなく,リスクも考慮すべきだ! 次の機会に,私が過去3年間の平均利回り30%だと言われてしまったら,気まずい質問に答えてください. <unk>の波動性はいくらか? <unk>. 次のブログでは,ヘッジファンドの実例を見てみましょう.

    ヘッジファンドの業績の分析例

    投資パフォーマンスを評価するには,リターン率だけでなく,リスク要因も考慮する必要があります. 今,ヘッジファンドの実例を見てみましょう. 下の表は,いくつかの有名な大型ヘッジファンドの平均年収です. (情報源:HSBC研究報告書). これらのファンドは,資産管理額が1億ドル以上で,開設期間は5年以上です.

表1

--	--
-	年間複合回収率
基金A	14.15%
基金B	15.17%
基金C	15.20%
基金D	79.17%
基金E	2.78%

金融危機の際に,何億ドルの利益を得て,負債型の商品を大々的に作って,危機から抜け出すポールソン・クレジット・オッポルニティズ・ファンド (Paulson Credit Opportunities Fund) を選んでください. このファンドを創設し,管理したポールソン (前米国財務長官のポールソンと同名だが,関係はない) は,最も有名なファンドマネージャーの一人になりました.

しかし,私たちは,リターン率だけでなく,リスクも考慮すべきだと議論しました. 表2は,各ファンドの波動性とシャープ比率の評価を列挙しています.

表2

-	年間複合回収率	収益率の変動	シャープ比率
基金A	14.15%	5.94%	1.9
基金B	15.17%	12.30%	1.0
基金C	15.20%	4.53%	2.7
Paulson Credit Opportunities	79.17%	49.83%	1.5
基金E	2.78%	12.21%	<0

波動性とシャープ比率の観点から分析すると,状況は少し複雑である.基金Cのリターンは15%であるにもかかわらず,波動性は5%未満であるため,シャープ比率は2.7であり,ポールソンファンドの1.5のほぼ2倍です! 言い換えれば,基金Cの波動性はポールソンファンドの波動性のわずか10分の1です.

基金Cは,Millennium Intl Ltd ((千<unk>年基金),ヘッジファンド業界の常緑樹であり,そのマネージャーの中には中国人の優秀者が何人かいた.投資家の観点から,得意なポルソン基金か,安定した千<unk>年基金か,どちらかを選ぶのは少し難しい.また,基金Aと基金Bのシャープ比率は米国株式市場の0.4を明らかに上回り,良い投資オプションでもある.基金Eのリターンは無リスク利率よりも低いので,限界はあまりにも低い.

シャープ比率だけで比較すると,ポルソン基金の<unk>には不公平な<unk>のように見える:波動性が高いが,主に<unk>は上向きの波動<unk>であり,収益<unk>の過程で発生する<unk>はリスクではない.投資家はお金を失うことを恐れている,特に一回の損失の数十パーセント.したがって,リスクの測定は,最大<unk>落<unk>,すなわち,各基金の歴史上最高点から<unk>落<unk>の最大比率も考慮すべきである.表3を参照.

表3

-	年間複合回収率	収益率の変動	シャープ比率	最大値下がり (発生時間)
Bluecrest	14.15%	5.94%	1.9	-4.83% （2003）
FORE (フロンティア・キャピタル)	15.17%	12.30%	1.0	-27.01%（2008）
ミレニアム	15.20%	4.53%	2.7	-7.24% （1998）
Paulson Credit Opportunities	79.17%	49.83%	1.5	-10.41%（2007）
Drake	2.78%	12.21%	<0	-51.74%（2007-2009）

資金A (ブルークレスト・キャピタル) の最大の減額は5%未満で,2003年に発生した. 資金Aは2007-2008年の大恐慌で大きな損失を回避した. 魅力的だ. ブルクレストと千<unk>年は,両者とも,二次融資の危機から逃れた,安定したタイプである.

ポールソン基金と比べると,春蘭秋<unk>,各勝地が優れていると言えます.したがって,三つの基金は機関投資家の好意の対象であり,管理資金はそれぞれ86億ドル,10億ドルおよび63億ドルに達しています.人びとに大金を稼ぐことは理にかなっているようです.注:多くの有名なシェルター<unk>基金は,リターン率を維持するために,新しい投資を受け付けません.

基金E ((Drake Absolute Return Fund) も数十億ドルを管理していた大型基金であったが,金融危機で50%以上を巨額の損失に遭い,投資家の信頼を失い,撤収し,Drakeが管理する資本は現在2億ドルしか残っていない.

最後に,基金Bを見てみよう.長期年収15%,シャープ比率1,综合指標はいいけど,2008年に一度は27%の損失を被ったが,危機をうまく乗り越えた.基金Bは相当な強さを持っていると言えます.それゆえ,それは数十億ドルを管理する大基金でもある.この基金の名前はFOREキャピタル (前線資本),<unk>の手Matthew Li (リュウ) は,中国人のヘッジファンド界の旗の一つです.

投資結果を評価するこの実例から,シャープ比率や最大下落などのリスク指標の有用性を見ることができます. 初心者投資家は,リスクを見ない,リターンを重んじることしかできません. ケリー公式もシャープ比率も,実は,私たちに,リターンとリスクのバランスを探すことを教えてくれます.

株式市場にはリスクがあり,慎重に投資する必要があります. 提供された情報は参考にのみであり,投資アドバイスではありません!

投稿者: シン・ドクキン