ナイーブベイズの興味深い理解

NavieBayes

  ニュース分類,患者分類など,多くの場合,分類が求められます. 視覚的な理解をするために,この記事では,実用的なアプリケーションから始め,シンプルな一般的な分類アルゴリズムである”ナヴィー・ベイズ・クラシフィアー”を紹介します.

• 01 患者の分類の例

ベイジアン分類器は簡単でわかりやすい例から始めましょう. ある病院では,午前中に6人の入院患者が診察を受けています.

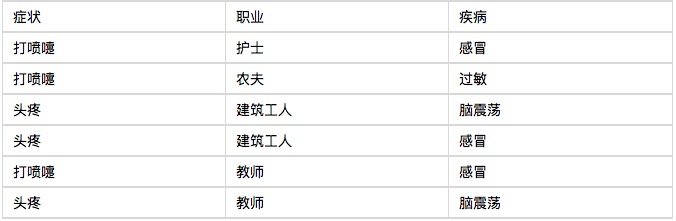
そして7人目の患者,噴気する建設労働者に インフルエンザの確率を尋ねて下さい.

  P(A|B) = P(B|A) P(A) / P(B)

ありがとうございました.

  P(感冒|打喷嚏x建筑工人) 
  　　　　= P(打喷嚏x建筑工人|感冒) x P(感冒) 
  　　　　/ P(打喷嚏x建筑工人)

“スプリンク”と”建設労働者”は独立していると考えます.

  P(感冒|打喷嚏x建筑工人) 
  　　　　= P(打喷嚏|感冒) x P(建筑工人|感冒) x P(感冒)
  　　　　/ P(打喷嚏) x P(建筑工人)

これは計算可能なことです.

  P(感冒|打喷嚏x建筑工人) 
  　　　　= 0.66 x 0.33 x 0.5 / 0.5 x 0.33 
  　　　　= 0.66

咳を吐いた建設労働者は66%の確率で風邪をひいたという結果です. 同様に,この患者がアレルギーや脳震を患っている確率も計算できます. これらの確率を比較すると,彼が最も罹患する可能性のある病気がわかります.

これがベージアン分類器の基本的方法である. 統計データに基づいて,特定の特性に基づいて,各カテゴリーの確率を計算し,分類を実現する.

• 02 素朴なベイズ分類器の公式

ある個体が,それぞれF1,F2,…,Fn.というnつの特性を有すると仮定し,それぞれC1,C2,…,Cm.というm個別カテゴリーが存在します.ベイエスの分類器は,確率が最も高い分類を計算するものです.つまり,以下の算数の最大値を求めます.

  P(C|F1F2...Fn) 
  　　   = P(F1F2...Fn|C)P(C) / P(F1F2...Fn)

P ((F1F2…Fn) はすべてのカテゴリーで同じなので,省略できます.

  P(F1F2...Fn|C)P(C)

値の最大値は

素朴なベアス分類器はさらに進み,全ての特性が互いに独立していると考え,したがって

  P(F1F2...Fn|C)P(C) 
  　　   = P(F1|C)P(F2|C) ... P(Fn|C)P(C)

上方方方程式の等号の右側の各項は,統計データから得られ,それによって各カテゴリに対応する確率を計算して,最大確率のクラスを見つけることができる.

“すべての特徴は相互に独立している”という仮説は,現実には成立する可能性は低いが,計算を大幅に簡素化することができ,分類結果の正確性に影響が少ないことを示す研究がある.

シンプルなベーイズ分類器の使い方については,以下の2つの例を参考にします.

• 03 アカウント分類

あるコミュニティのウェブサイトのサンプル統計によると,そのサイトで登録されている1万件のアカウントのうち,89%が本物 (設定C0),11%が偽物 (設定C1) である.

  C0 = 0.89 C1 = 0.11

このアカウントには以下の3つの特徴があります. F1:日記数/登録日数 F2:フレンド数/登録日数 F3:本物の頭像を使用するかどうか (本物の頭像は1,非本物の頭像は0) F1 = 0.1  F2 = 0.2  F3 = 0

このアカウントは実アカウントか偽アカウントか? シンプルなベアス分類器を使用して,以下の計算式の値を計算します.

P(F1|C)P(F2|C)P(F3|C)P©

上記の値は統計データから得られますが,問題があります.F1とF2は連続変数であり,特定の値に基づいて確率を計算するのは不適切です. 一つのテクニックは,連続値を離散値に変換して,区間の確率を計算することです. 例えば,F1を分解して[0, 0.05]、(0.05, 0.2)、[0.2, +∞] 3つの区間,そしてそれぞれの区間の確率を計算する. この例では,F1は0.1で,第2の区間に落ちるので,計算する時には第2の区間の確率を使用する.

統計によると,

P(F1|C0) = 0.5, P(F1|C1) = 0.1  P(F2|C0) = 0.7, P(F2|C1) = 0.2  P(F3|C0) = 0.2, P(F3|C1) = 0.9

だから

P(F1|C0) P(F2|C0) P(F3|C0) P(C0)  = 0.5 x 0.7 x 0.2 x 0.89  = 0.0623 P(F1|C1) P(F2|C1) P(F3|C1) P(C1)  = 0.1 x 0.2 x 0.9 x 0.11  = 0.00198 このアカウントは偽のアカウントの30倍以上も高い確率で,真偽のアカウントであると判断されます.

• 04 性別による分類

以下は人間の身体の特徴に関する統計です.

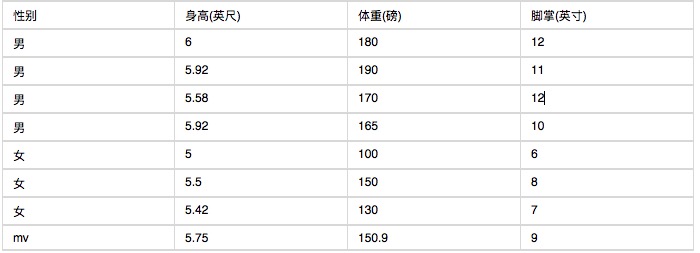
6フィートの身長,130ポンドの体重,8インチの足首の知られた人物は,男性か女性かを尋ねてください. 素朴なベアス分類器に基づいて,以下の式の値を計算してください。

P (身長・性別) x P (体重・性別) x P (脚・掌・性別) x P (性別)

ここで難しいのは,身長,体重,足首は連続変数であるため,離散変数による確率計算はできない.また,サンプルが少ないため,区間計算もできない.どうしよう.このとき,男性と女性の身長,体重,足首は正規分布であると仮定し,サンプルから平均値と方差を計算する.つまり正規分布の密度関数を得ることができる.密度関数があるので,代数値を入れ,ある点の密度関数の値を計算できる.例えば,男性の身長平均は5.855であり,方差は0.035の正規分布である.したがって,男性の身長6英尺の確率相関は1.5789である (これは1より大きいとは関係なく,ここは密度関数の値であり,個々の相関の可能性を反映するだけである).

このデータから,性別の分類を計算できます.

P (身長=6人の男性) x P (体重=130人の男性) x P (足元=8人の男性) x P (男性)

= 6.1984 x e-9

P (身長=6人の女性) x P (体重=130人の女性) x P (手のひら=8人の女性) x P (女性)

= 5.3778 x e-4

女性は男性より約1万倍も高い確率で女性であると判断できるのです.

一峰からの微信公用番号