KNNアルゴリズムに基づくベイズ分類器

分類決定を行う分類器を設計する理論的基礎 ベイジアン決定理論:

比較P ((ωi) の定義は,P ((ωi) の定義は,このデータの特性のベクトルが既知である場合に,そのデータがiの属性である確率は何であるかを表す.これは後証確率となる.ベイエスの公式によれば,次のように表すことができる.

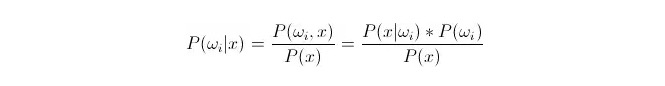
その中,P ((x) の確率ωi) は,似似似確率または類条件確率と呼ばれている.P ((ωi) は,実験とは関係なく,実験前に知られるので,先制確率と呼ばれている.

分類する際には,与えられた x の場合,後検定確率 P ((ωi) のx) を最大にするカテゴリーを選択することができる.各カテゴリーで P ((ωi) のx) が小さい場合,ωi は変数で,x は定数である.したがって,P ((ωi) のx) を除き,考慮しないことができる.

計算すると,P (x) は*P ((ωi) の問題。 予期確率 P ((ωi) は,統計訓練が集中して各分類の下に現れるデータの比率である限りよい.

概率P ((x Berdosaωi) の計算は,このxがテスト集のデータであるため,費用を省略する.訓練集のデータから直接得ることは不可能である.

以下は k 近隣アルゴリズム (英語: KNN) について紹介する.

訓練集積のデータ x1,x2…xn (それぞれのデータが m 次元) に基づいて,このデータの分布を,クラスωiで適合させたい. x を m 次元空間の任意の点として設定して,P ((x ∈ωi) をどのように計算するか?

データ量が十分に大きい場合,比例的に近似確率を用いることができる.この原理を利用して,点xの周りに,点xから最も近いk個のサンプルポイントを特定し,そのうちのどれがカテゴリiに属しているかを調べる.このk個のサンプルポイントを囲む最小の超球の体積Vを計算し,さらに,すべてのサンプルデータの中でωiカテゴリに属している数 Ni を求める.

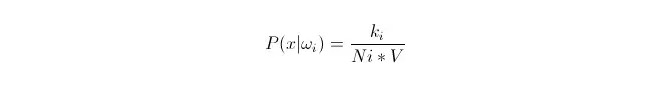
xの点における クラス条件の確率の密度です.

P (ωi) は何ですか? 上記の方法に従って,P ((ωi) =Ni/N 。その中のNはサンプル総数。 そして,P (x) = k (n)*V) で, k はこの超球体を取り巻くすべてのサンプルの点の数;N はサンプルの総数である. 計算すると,P (ωigadgadx) は,

P(ωi|x)=ki/k

上述の式をさらに説明すると, V サイズの超球体の中に, k 個のサンプルを囲み,その中から i 類に属する ki があります。 このように,包囲されたどの種類のサンプルが最も多いか,私たちは,ここでの x がどの類に属すべきかを判断します。 これが k 近隣アルゴリズムで設計された分類器です。