脳内のサポートベクターマシン

支持ベクトルマシン (SVM) は,重要な機械学習分類器であり,非線形変数の巧妙な使用により,低次元特性を高次元に投影し,より複雑な分類タスクを実行できます. SWMは,数学的な技巧を使用しているように見えますが,実は,脳のコーディングのメカニズムに合致します. 2013年のNatureの論文から,機械学習と脳の働きの原理の深いつながりを理解することができます. 論文名:複雑な認知のタスクにおける混合選択性の重要性 (by Omri Barak al. )

• #### SVM

この驚くべき連結はどこから来るのか? まず,神経コードの本質についてお話ししましょう. 動物は特定の信号を受け取り,それに応じて特定の行動をします.一つは,外界の信号を神経電気信号に変換し,もう一つは,神経電気信号を決定信号に変換します.前回のプロセスは,エンコーディングと呼ばれ,後回のプロセスは,解読され,そして,神経電気信号の真の目的は,解読され,その後決定を行うことです.したがって,機械学習による視覚解読のコードは,最も簡単な方法は,分類器,あるいは,論理的モデルの線形分類器で,入力信号を特定の特性の分類によって分類して扱うことです. 例えば,老虎が逃げるのを見たり,サメが餌を食うのを見たり,もちろん,時々,それはうまくいきます. 例えば,神経信号が最終的に運動に変換され,ほとんどの神経信号の分類をシグナルに変換する必要があり,その連続的な動きをシグナルにシグナルに変換します.

ニューロンのコードの仕組みを見てみましょう. まず,ニューロンは基本的には, 抵抗と容量を外電圧で調整するRC回路として見ることができます. 外部信号が十分に大きくなったら, 伝導され, 閉められ, 特定の時間内に放電する周波数で 信号を表現します. そして,私たちはコードの話をします. 時間の分散処理をすることがよくあります. 時間の小さな窓の中で,放電率は不変です.

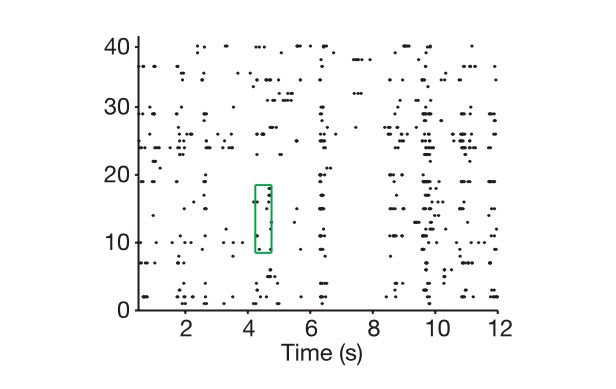
縦軸は細胞 横軸は時間です この図は 神経コードの抽出方法を示しています

もちろん,N次元ベクトルとニューロンのコードの実際の次元には 違いがありますが,どうやってニューロンのコードの実際の次元を定義しますか? まず,このN次元ベクトルでマークされたN次元空間に入ります. そして,可能なすべてのタスクの組み合わせを用意します. 例えば,このN次元ベクトルでマークされたN次元空間に入ります. 想像してください,この画像が世界全体を表している1000枚の画像をあなたに示すとしましょう. そして,その1枚のニューロンのコードを,このスペースの1つのポイントとしてマークします. そして,この1000個のポイントを構成するサブスペースの次元を,ベクトル代数学的思考で捉えます. つまり,このニューロンの表記の実際の次元です.

暗号の実際の寸法に加えて,私たちは,外部信号の実際の寸法という概念があります. 信号は,神経ネットワークによって表現された外部信号です. もちろん,外部信号のすべての詳細を繰り返す必要があります. それは無限の問題です. しかし,私たちの分類と決定の基礎は,常に重要な特征であり,縮小プロセスです. これはPCAの考えです.

科学者達が直面する根本的な問題は なぜこの問題を 本質的な問題より 遥かに高い プログラミングの次元や ニューロンの数で 解決するのかということです

計算の神経科学と機械学習は ニューロンの高次元の特性が 強い学習能力の基礎であると教えてくれます プログラミングの次元が高くなるほど 学習能力も高まります 注目してください ディープネットワークも触れてはいません なぜでしょうか? ニューロンのコードの仕組みは SVMのような原理で 低次元の信号を高次元のものに投影すると できるだけ多くの分類ができます 線形的な分類器であっても 数え切れないほどの問題を解くことができます

ここで論じられている神経コードは,より上級の神経センターの神経コードを主に指していることに注意してください.例えば,文章で論じられている前額頭前皮質 (Prefrontal Cortex) ((PFC) は,より下級の神経センターのコード法が分類と意思決定にあまり関与していないからです.

PFCが代表する脳の高級領域

神経コードの謎は,Nのニューロン数とKの次元との関係で明らかになる (この差は200倍にも達する).なぜ見かけに余剰のニューロン数で質の飛躍を起こすのか? まず,私たちは,コードの次元が現実のタスクの重要な変数の次元に等しいときに,線形分級器を使用すると,非線形分級器を使用できないと仮定します (例えば,西瓜から西瓜を分離する場合は,線形の境界で西瓜から西瓜を分離することはできません).これは,深層学習とSVMが機械学習に入っていないときに解決するのが難しい典型的な問題です.この種の問題のSVMの核心解法を再表示として使用します.つまり,私たちの元の座標系を新しい高次元座標系に変更すると,超線形分級器を使用できます. (これは,たとえ,あなたがシグナルとシグナルに配置されていても,このグラフに表示できます.

SVMはベクトルマシンをサポートしています.

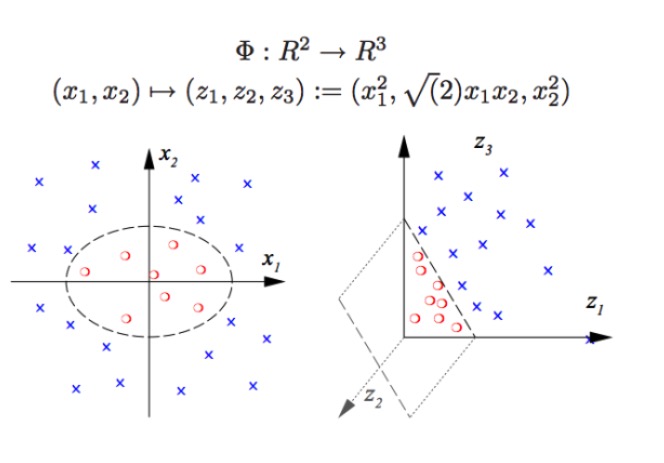
SVMは非線形分類を行うことができる.例えば,図の赤い点と青い点を分離する.線形境界では,赤い点と青い点を分離することができない (左図),したがってSVMの方法は,次元を高めることである.ただ単に変数の数を追加するだけでは,行われない.例えば, (x1,x2) を (x1,x2,x1+x2) システムにマッピングすることは,実際には二次元の線形空間である (図を描く場合,赤の点と青の点は同じ平面にある),非線形関数 (x1^2,x1) しか使わない.*x2,x2^2で,本質的な低次元から高次元への移行が起こります. 青い点を空中に投げて, 青い点を赤い点から切り離す平面を描きます.

実際,実際のニューラルネットワークがやっていることは,まさにそれと同じです.このような線形分類器 (解読器) が行うことができる分類の種類は,大きく増加しました.つまり,私たちは,以前よりもはるかに強力なパターン認識能力を得ました.ここでは,高次元は高エネルギーであり,高次元打撃は真実です.

ニューロンのコードの高次元はどのように得られますか? 光ニューロンの個数が多すぎることは役に立たないのです. 線形代数学の知識からわかるのは,もし,膨大な数のN個のニューロンがいて,それぞれの放電率がKの鍵特征と線形的に関係している場合,最終的に表現する次元は問題そのものの次元に等しく,あなたのN個のニューロンは役に立たないのです. (その余剰ニューロンはKのニューロンの線形的な組成である) この点を突破するには,Kの特征と非線形的に関係するニューロンが必要です.ここでは非線形混合型ニューロンが呼ばれます. この種のニューロンの表現は非常に複雑で,その原理はSVMの中核に非線形要素を含む正の関数に似ています.これらの非線形ニューロンがあれば,シンフォニーコードの特征の次元を突破する能力を持つニューロンは,特征の次元をタスクできます.

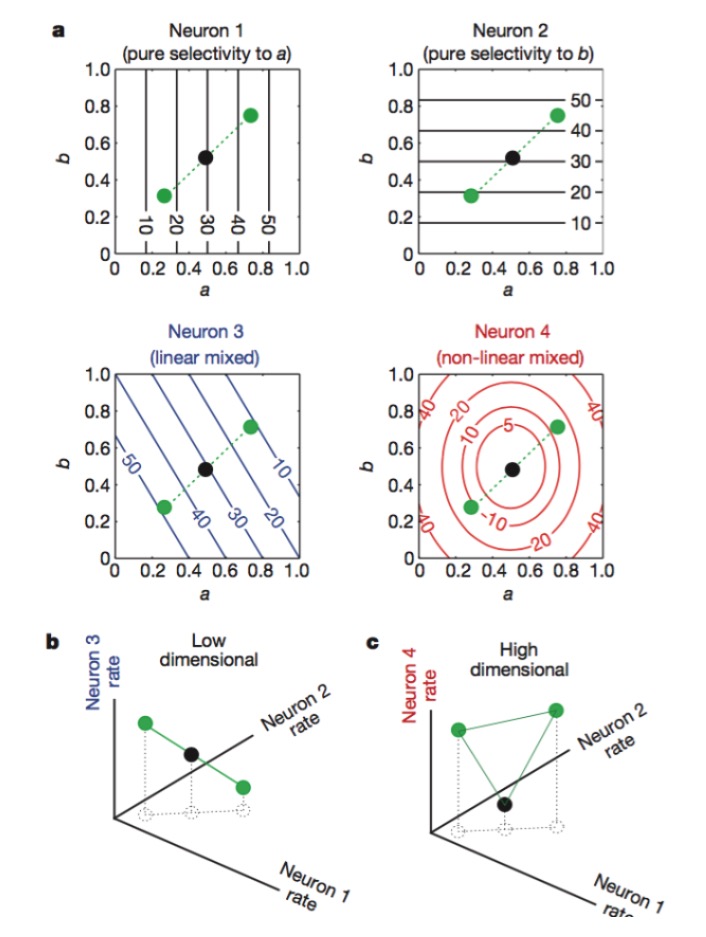
図:ニューロン1と2は,それぞれ特征aとbにのみ敏感であり,3は特征aとbの線形混合に敏感であり,4は特征の非線形混合に敏感である.最終的にニューロン1,2,4の組み合わせだけがニューロンのコードの次元を上昇させる (下図).

このコードの公式は混合コード (mixed selectivity) と呼ばれ,このコードの原理が解明されていなかった時,理解できないと思われたのは,ある種の信号に対する神経ネットワークの反応が乱雑だったからです.周囲の神経系では,神経細胞はセンサーのように働き,信号の異なる特性を抽出し,パターンを認識します.各神経細胞の機能はかなり特殊で,例えば,視網膜のrodsとconesは光子を受信し,それからGangelion cellはコードを書き続けます.各ニューロンは,専門的に訓練された哨兵のようなものです.しかし,脳の高級領域では,この明確な区別は難しいです.同じニューロンは,さまざまな特性に敏感であり,この種の感受性は線形ではありません.

自然界のあらゆる細部に 玄関があり 多量の冗長性があり 混同コードが混ざり合っているように見える 混沌とした信号が コンピュータの性能を向上させるのです この原理を踏まえたら こんなタスクを簡単にこなせるのです

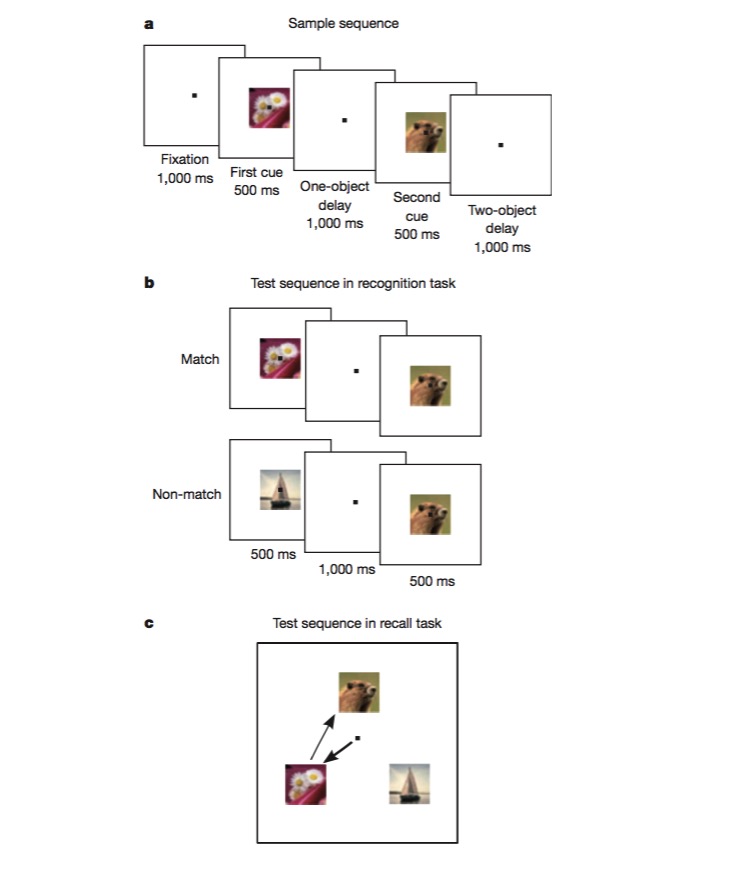
このタスクでは,は最初に画像がそれと同じかどうかを識別するように訓練され,その後2つの異なる画像が現れる順序を判断するように訓練される.は,このようなタスクを完了するために,タスクの異なる側面をコードすることができる必要があります.例えば,タスクのタイプ,画像の種類など.これは,混合非線形コーディングメカニズムが存在するかどうかをテストする優れた実験である.実験では,大量のニューロンが混合特性に敏感であり,非線形が存在することを確認した.例えば,同じことが花のコーディングであり,ニューロンの放電の強さは,タスクがrecallかrecognitionか,特性の間で独立しないかに依存する.混合コーディングは,ニューロンのコーディングを高次元の特性を有するので,これらの複数の側面を含むタスクとコードの処理を容易にする.

この記事を見て, デザインニューラルネットワークは, 非線形の要素を導入すれば, パターン認識の能力を大きく向上させると学びました. そして,SVMは,これを非線形の分類の問題に当てはめて, 計算神経科学と機械学習は,コインの2面のようなものです.

脳の領域の機能を研究し,まず機械学習の方法を使ってデータを処理し,例えばPCAで問題の重要な次元を見つけ,次に機械学習パターンを認識する思考で 神経コードを解読する.最終的に,新しいインスピレーションを得れば,機械学習の方法を改善することができます.脳や機械学習アルゴリズムにとって,最終的に最も重要なのは,情報を最も適切な表現方法を得ることであり,良い表現があれば,何でも簡単です.これは,機械学習の線形的な論理から量的な機械への支援に戻り,深層学習への段階的な進化のプロセスです.おそらくこれは,私たちが世界に対するますます高い制御能力を得るために進化した脳のプロセスです. あるいは,進化の目的は,誰が老虎で誰が羊で,誰が食べることができるかをより明確に理解することであり,その過程で,世界自身を理解し,そして,世界自身を理解し,その過程で,熱意を深く理解し,その過程で発展しています.

ジュン・クレイズ船の技術