Python ナイーブベイズアプリケーション

予測変数の相互独立を前提とする場合,ベイエスの定理に基づいて素朴ベイエスの分類法が得られる.より簡単に言えば,素朴ベイエスの分類者は,分類の特性がその分類の他の特性と無関係であると仮定する.例えば,果物が丸く赤く,直径が約3インチであれば,その果物はリンゴである可能性がある.これらの特性が相互依存している場合でも,または他の特性に依存している場合でも,素朴ベイエスの分類者は,これらの特性がそれぞれ独立して存在すると仮定し,この果物がリンゴであることを示唆する.

• #### シンプル・ベーイズモデルは簡単に構築でき,大規模なデータセットに非常に有用である.シンプルであるにもかかわらず,シンプル・ベーイズモデルは,非常に複雑な分類方法を超えたパフォーマンスを発揮する.

ベイズの定理は,P ©,P (x),P (x) とP (x) とc) から後証確率P © とx) を計算する方法を提供する.以下の方程式を参照してください.

“このままでは,

P © は,既知の予測変数 (属性) を前提として,クラス (目標) の後行確率である. P (© は,そのクラスの先制確率である. P ((xfin_Latnfin_Latnfin_Latnfin_Latnfin_Latnfin_Latnfin_Latnfin_Latnfin_Latn Yksi) on todennäköisyys, joka ennustaa muuttujan, jos se on tunnettu. P (x) は,予測変数の先導確率である. 例:この概念を例で説明しましょう. 下に,私は天候のトレーニングセットと,それに対応するターゲット変数であるPlayを持っています. 今,私たちは天候の状況によって,遊びをしたり,遊びをしない参加者を分類する必要があります. 次のステップを実行しましょう.

ステップ1:データセットを周波数表に変換する

ステップ2:Overcastの確率が0.29で,プレイの確率が0.64であるような確率を利用して,Likelihood表を作成する.

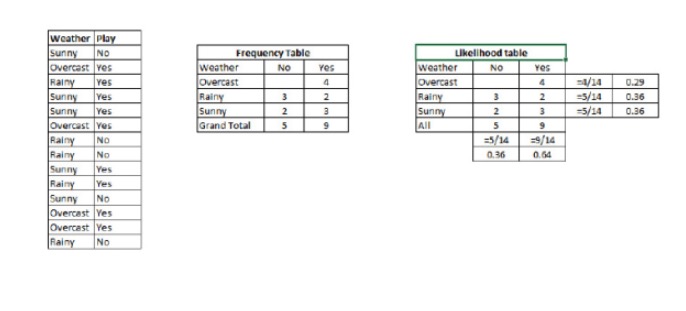
ステップ3: 素朴なベーイズ式を使って,それぞれのクラスの後続確率を計算する.後続確率が最も大きいクラスは,予測された結果である.

質問: 晴れた天気であれば,参加者は遊びます. この記述は正しいですか?

P=P (P (P (P (P)) =P (P (P (P)) =P (P (P (P)) =P (P (P)) =P (P (P (P)) =P (P (P)) =P (P (P)) =P (P (P)) =P (P (P)) =P (P (P)) =P (P (P)) =P (P (P)) =P (P (P)) =P (P (P)) =P (P (P)) =P (P)) =P (P (P)) =P (P)) =P (P (P)) =P (P (P)) =P (P (P)) =P (P (P)) =P (P (P)) =P (P) =P (P) =P (P) =P (P) =P (P) =P (P) =P (P (P) =P (P) =P (P) =P (P (P) =P (P) =P (P) =P (P) =P (P) =P (P) =P (P) =P (

P=³⁄₉=0.33です. P=⁵⁄₁₄=0.36です. P=⁹⁄₁₄=0.64.

これは,P (P) =0.33 * 0.64 / 0.36 = 0.60 の確率です.

素朴なベアスは,異なる属性によって異なるカテゴリーの確率を予測する類似した方法を使用した.このアルゴリズムは,テキスト分類や,複数のカテゴリーに関する問題で一般的に使用されている.

• #### Pythonのコード:

  #Import Library
  from sklearn.naive_bayes import GaussianNB
  　　
  #Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset

Create SVM classification object model = GaussianNB()

there is other distribution for multinomial classes like Bernoulli Naive Bayes, Refer link

Train the model using the training sets and check score

model.fit(X, y) #Predict Output predicted= model.predict(x_test)