前回の記事では、さまざまな仲値計算方法についての予備的な紹介と仲値に関する改訂を行いました。この記事では、このトピックについて引き続き掘り下げていきます。

必要なデータ

注文フローデータと 10 レベルの深度データは実際の取引から収集され、更新頻度は 100 ミリ秒です。実際の市場には、リアルタイムで更新される売買データのみが含まれています。簡略化のため、現時点では使用されていません。データが大きすぎることを考慮して、詳細なデータは 100,000 行のみ保持され、各レベルの市況も別々の列に分割されます。

from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import ast
%matplotlib inline

tick_size = 0.0001

trades = pd.read_csv('YGGUSDT_aggTrade.csv',names=['type','event_time', 'agg_trade_id','symbol', 'price', 'quantity', 'first_trade_id', 'last_trade_id',
       'transact_time', 'is_buyer_maker'])

trades = trades.groupby(['transact_time','is_buyer_maker']).agg({
    'transact_time':'last',
    'agg_trade_id': 'last',
    'price': 'first',
    'quantity': 'sum',
    'first_trade_id': 'first',
    'last_trade_id': 'last',
    'is_buyer_maker': 'last',
})

trades.index = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index.rename('time', inplace=True)
trades['interval'] = trades['transact_time'] - trades['transact_time'].shift()

depths = pd.read_csv('YGGUSDT_depth.csv',names=['type','event_time', 'transact_time','symbol', 'u1', 'u2', 'u3', 'bids','asks'])

depths = depths.iloc[:100000]

depths['bids'] = depths['bids'].apply(ast.literal_eval).copy()
depths['asks'] = depths['asks'].apply(ast.literal_eval).copy()

def expand_bid(bid_data):
    expanded = {}
    for j, (price, quantity) in enumerate(bid_data):
        expanded[f'bid_{j}_price'] = float(price)
        expanded[f'bid_{j}_quantity'] = float(quantity)
    return pd.Series(expanded)
def expand_ask(ask_data):
    expanded = {}
    for j, (price, quantity) in enumerate(ask_data):
        expanded[f'ask_{j}_price'] = float(price)
        expanded[f'ask_{j}_quantity'] = float(quantity)
    return pd.Series(expanded)
# 应用到每一行，得到新的df
expanded_df_bid = depths['bids'].apply(expand_bid)
expanded_df_ask = depths['asks'].apply(expand_ask)
# 在原有df上进行扩展
depths = pd.concat([depths, expanded_df_bid, expanded_df_ask], axis=1)

depths.index = pd.to_datetime(depths['transact_time'], unit='ms')
depths.index.rename('time', inplace=True);

trades = trades[trades['transact_time'] < depths['transact_time'].iloc[-1]]

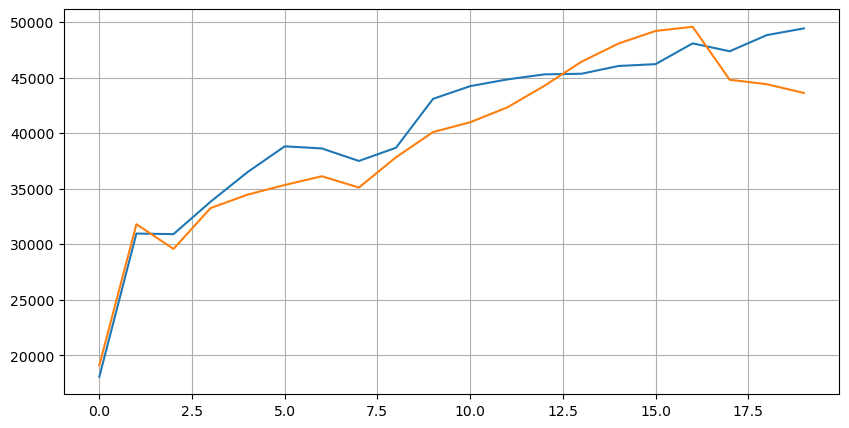
まずはこの20の市況の分布を見てみましょう。予想通りですね。市場のオープンから遠いほど保留注文が多く、買い注文と売り注文はほぼ対称的になっています。

bid_mean_list = []
ask_mean_list = []
for i in range(20):
    bid_mean_list.append(round(depths[f'bid_{i}_quantity'].mean(),0))
    ask_mean_list.append(round(depths[f'ask_{i}_quantity'].mean(),0))
plt.figure(figsize=(10, 5))
plt.plot(bid_mean_list);
plt.plot(ask_mean_list);
plt.grid(True)

深度データとトランザクションデータを組み合わせることで、予測精度の評価が容易になります。ここでは、トランザクション データが深度データよりも後であることを確認します。遅延を考慮せずに、予測値と実際のトランザクション価格の間の平均二乗誤差を直接計算します。予測の精度を測定するために使用されます。

結果から判断すると、売買ペアの平均である mid_price の誤差が最も大きいことがわかります。weight_mid_price に変更すると、誤差はすぐに大幅に小さくなり、加重平均価格を調整することでさらに改善されます。昨日の記事が公開された後、I^³⁄₂ のみを使用したという報告がありました。こちらで確認したところ、結果がより良好であることがわかりました。理由を考えてみると、それはイベントの頻度の違いであるはずです。Iが-1と1に近い場合、それは低確率のイベントです。これらの低確率を修正するために、高頻度のイベントの予測あまり正確ではありません。したがって、高頻度のイベントに対処するために、いくつかの調整を行いました（これらは純粋に実験的なパラメータであり、実際の取引にはあまり役立ちません）。

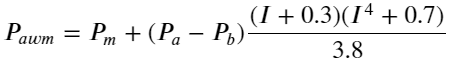
結果は若干良くなりました。前回の記事でも述べたように、戦略はより多くのデータで予測する必要があります。より深いデータと注文履行データでは、市場価格との絡み合いによって得られる改善はすでに非常に弱いです。

df = pd.merge_asof(trades, depths, on='transact_time', direction='backward')

df['spread'] = round(df['ask_0_price'] - df['bid_0_price'],4)
df['mid_price'] = (df['bid_0_price']+ df['ask_0_price']) / 2
df['I'] = (df['bid_0_quantity'] - df['ask_0_quantity']) / (df['bid_0_quantity'] + df['ask_0_quantity'])
df['weight_mid_price'] = df['mid_price'] + df['spread']*df['I']/2
df['adjust_mid_price'] = df['mid_price'] + df['spread']*(df['I'])*(df['I']**8+1)/4
df['adjust_mid_price_2'] = df['mid_price'] + df['spread']*df['I']*(df['I']**2+1)/4
df['adjust_mid_price_3'] = df['mid_price'] + df['spread']*df['I']**3/2
df['adjust_mid_price_4'] = df['mid_price'] + df['spread']*(df['I']+0.3)*(df['I']**4+0.7)/3.8

print('平均值     mid_price的误差：', ((df['price']-df['mid_price'])**2).sum())
print('挂单量加权 mid_price的误差：', ((df['price']-df['weight_mid_price'])**2).sum())
print('调整后的   mid_price的误差：', ((df['price']-df['adjust_mid_price'])**2).sum())
print('调整后的 mid_price_2的误差：', ((df['price']-df['adjust_mid_price_2'])**2).sum())
print('调整后的 mid_price_3的误差：', ((df['price']-df['adjust_mid_price_3'])**2).sum())
print('调整后的 mid_price_4的误差：', ((df['price']-df['adjust_mid_price_4'])**2).sum())

平均值     mid_price的误差： 0.0048751924999999845
挂单量加权 mid_price的误差： 0.0048373440193987035
调整后的   mid_price的误差： 0.004803654771638586
调整后的 mid_price_2的误差： 0.004808216498329721
调整后的 mid_price_3的误差： 0.004794984755260528
调整后的 mid_price_4的误差： 0.0047909595497071375

2速ギアの深さを考慮する

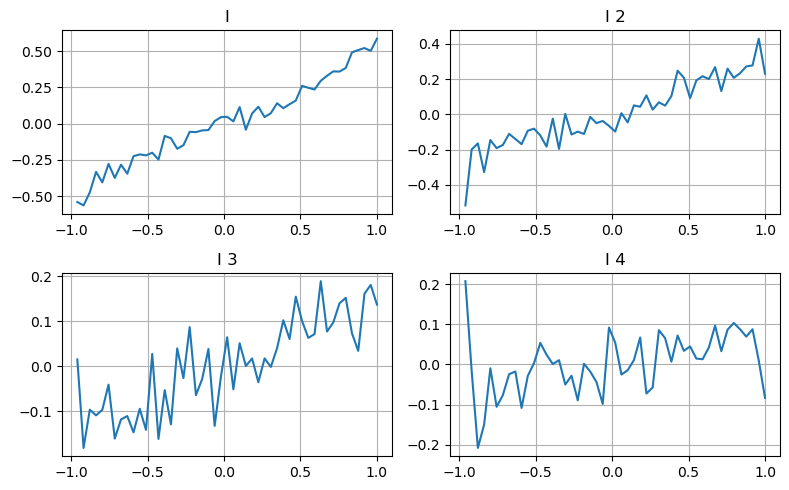
ここでは、前回の記事のアイデアを使用して、特定の影響パラメータのさまざまな値の範囲と取引価格の変化を調べ、このパラメータが中間価格にどのように寄与しているかを測定します。第 1 レベルの深さのグラフに示されているように、I が増加すると、次の取引価格がプラスに変化する可能性が高くなり、これは I がプラスの貢献をしていることを意味します。

2 回目の処理も同様に行われ、効果は 1 回目の処理よりもわずかに小さくなったものの、依然として無視できないことが判明しました。 3 番目の深さレベルもわずかに寄与しますが、単調性ははるかに悪く、より深い深さは基本的に参照価値がありません。

異なる寄与レベルに応じて、3 つのレベルの不均衡パラメータに異なる重みが割り当てられます。実際の検査では、異なる計算方法で予測誤差がさらに減少することが示されています。

bins = np.linspace(-1, 1, 50)
df['change'] = (df['price'].pct_change().shift(-1))/tick_size
df['I_bins'] = pd.cut(df['I'], bins, labels=bins[1:])
df['I_2'] = (df['bid_1_quantity'] - df['ask_1_quantity']) / (df['bid_1_quantity'] + df['ask_1_quantity'])
df['I_2_bins'] = pd.cut(df['I_2'], bins, labels=bins[1:])
df['I_3'] = (df['bid_2_quantity'] - df['ask_2_quantity']) / (df['bid_2_quantity'] + df['ask_2_quantity'])
df['I_3_bins'] = pd.cut(df['I_3'], bins, labels=bins[1:])
df['I_4'] = (df['bid_3_quantity'] - df['ask_3_quantity']) / (df['bid_3_quantity'] + df['ask_3_quantity'])
df['I_4_bins'] = pd.cut(df['I_4'], bins, labels=bins[1:])
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(8, 5))


axes[0][0].plot(df.groupby('I_bins')['change'].mean())
axes[0][0].set_title('I')
axes[0][0].grid(True)

axes[0][1].plot(df.groupby('I_2_bins')['change'].mean())
axes[0][1].set_title('I 2')
axes[0][1].grid(True)

axes[1][0].plot(df.groupby('I_3_bins')['change'].mean())
axes[1][0].set_title('I 3')
axes[1][0].grid(True)

axes[1][1].plot(df.groupby('I_4_bins')['change'].mean())
axes[1][1].set_title('I 4')
axes[1][1].grid(True)
plt.tight_layout();

df['adjust_mid_price_4'] = df['mid_price'] + df['spread']*(df['I']+0.3)*(df['I']**4+0.7)/3.8
df['adjust_mid_price_5'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.3*df['I_2'])/2
df['adjust_mid_price_6'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.3*df['I_2'])**3/2
df['adjust_mid_price_7'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.3*df['I_2']+0.3)*((0.7*df['I']+0.3*df['I_2'])**4+0.7)/3.8
df['adjust_mid_price_8'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.2*df['I_2']+0.1*df['I_3']+0.3)*((0.7*df['I']+0.3*df['I_2']+0.1*df['I_3'])**4+0.7)/3.8

print('调整后的 mid_price_4的误差：', ((df['price']-df['adjust_mid_price_4'])**2).sum())
print('调整后的 mid_price_5的误差：', ((df['price']-df['adjust_mid_price_5'])**2).sum())
print('调整后的 mid_price_6的误差：', ((df['price']-df['adjust_mid_price_6'])**2).sum())
print('调整后的 mid_price_7的误差：', ((df['price']-df['adjust_mid_price_7'])**2).sum())
print('调整后的 mid_price_8的误差：', ((df['price']-df['adjust_mid_price_8'])**2).sum())

调整后的 mid_price_4的误差： 0.0047909595497071375
调整后的 mid_price_5的误差： 0.0047884350488318714
调整后的 mid_price_6的误差： 0.0047778319053133735
调整后的 mid_price_7的误差： 0.004773578540592192
调整后的 mid_price_8的误差： 0.004771415189297518

取引データを考慮する

取引データはロングポジションとショートポジションの度合いを直接反映します。結局のところ、これは実際のお金が絡むオプションであり、注文を出すコストははるかに低く、意図的な注文の詐欺のケースさえあります。したがって、中間価格を予測する場合、戦略は取引データに焦点を当てる必要があります。

形式を考慮して、注文平均到着数量不均衡を定義します。VI、Vb、Vs は、それぞれ単位イベント内の買い注文と売り注文の平均数量を表します。

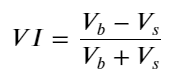
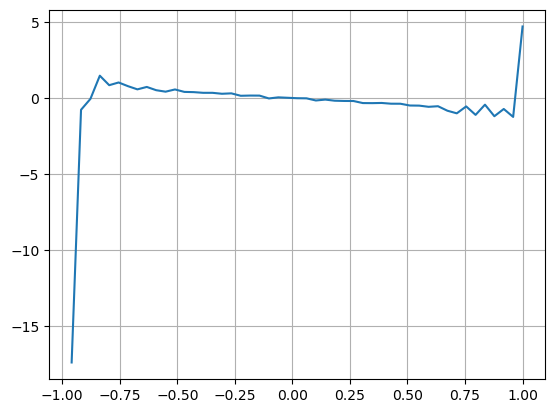
結果は、短期間の到着量が価格変動を予測する上で最も重要であることを示しています。VIが（0.1-0.9）の間の場合、価格と負の相関がありますが、範囲外では価格と正の相関があります。価格。これは、市場が極端でない場合は主に変動が特徴で、価格は平均に戻ることを示唆しています。大量の買い注文が売り注文を圧倒するなど、極端な市場状況が発生すると、トレンドはトレンドから外れます。 。これらの低確率の状況を無視し、トレンドと VI が負の線形関係を満たすと単純に仮定した場合でも、中間価格の予測誤差は大幅に減少します。式中のaは係数を表します。

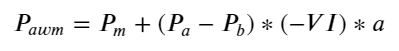
alpha=0.1

df['avg_buy_interval'] = None
df['avg_sell_interval'] = None
df.loc[df['is_buyer_maker'] == True, 'avg_buy_interval'] = df[df['is_buyer_maker'] == True]['transact_time'].diff().ewm(alpha=alpha).mean()
df.loc[df['is_buyer_maker'] == False, 'avg_sell_interval'] = df[df['is_buyer_maker'] == False]['transact_time'].diff().ewm(alpha=alpha).mean()

df['avg_buy_quantity'] = None
df['avg_sell_quantity'] = None
df.loc[df['is_buyer_maker'] == True, 'avg_buy_quantity'] = df[df['is_buyer_maker'] == True]['quantity'].ewm(alpha=alpha).mean()
df.loc[df['is_buyer_maker'] == False, 'avg_sell_quantity'] = df[df['is_buyer_maker'] == False]['quantity'].ewm(alpha=alpha).mean()

df['avg_buy_quantity'] = df['avg_buy_quantity'].fillna(method='ffill')
df['avg_sell_quantity'] = df['avg_sell_quantity'].fillna(method='ffill')
df['avg_buy_interval'] = df['avg_buy_interval'].fillna(method='ffill')
df['avg_sell_interval'] = df['avg_sell_interval'].fillna(method='ffill')

df['avg_buy_rate'] = 1000 / df['avg_buy_interval']
df['avg_sell_rate'] =1000 / df['avg_sell_interval']

df['avg_buy_volume'] = df['avg_buy_rate']*df['avg_buy_quantity']
df['avg_sell_volume'] = df['avg_sell_rate']*df['avg_sell_quantity']

df['I'] = (df['bid_0_quantity']- df['ask_0_quantity']) / (df['bid_0_quantity'] + df['ask_0_quantity'])
df['OI'] = (df['avg_buy_rate']-df['avg_sell_rate']) / (df['avg_buy_rate'] + df['avg_sell_rate'])
df['QI'] = (df['avg_buy_quantity']-df['avg_sell_quantity']) / (df['avg_buy_quantity'] + df['avg_sell_quantity'])
df['VI'] = (df['avg_buy_volume']-df['avg_sell_volume']) / (df['avg_buy_volume'] + df['avg_sell_volume'])

bins = np.linspace(-1, 1, 50)
df['VI_bins'] = pd.cut(df['VI'], bins, labels=bins[1:])
plt.plot(df.groupby('VI_bins')['change'].mean());
plt.grid(True)

df['adjust_mid_price'] = df['mid_price'] + df['spread']*df['I']/2
df['adjust_mid_price_9'] = df['mid_price'] + df['spread']*(-df['OI'])*2
df['adjust_mid_price_10'] = df['mid_price'] + df['spread']*(-df['VI'])*1.4

print('调整后的mid_price   的误差：', ((df['price']-df['adjust_mid_price'])**2).sum())
print('调整后的mid_price_9 的误差：', ((df['price']-df['adjust_mid_price_9'])**2).sum())
print('调整后的mid_price_10的误差：', ((df['price']-df['adjust_mid_price_10'])**2).sum())

调整后的mid_price   的误差： 0.0048373440193987035
调整后的mid_price_9 的误差： 0.004629586542840461
调整后的mid_price_10的误差： 0.004401790287167206

総合平均価格

保留中の注文と取引データの両方が中間価格を予測するのに役立つことを考慮すると、これら2つのパラメータを組み合わせることができます。ここでの重み付けは任意であり、境界条件は考慮されません。極端な場合、予測される中間価格は買いと売りの違いはありますが、誤差が軽減できる限り、これらの詳細は重要ではありません。

最終的に、予測誤差は最初の0.00487から0.0043に減少しました。ここでは詳細には触れません。中間価格についてはまだ調査すべきことがたくさんあります。結局のところ、中間価格を予測することは価格を予測することです。自分で試してみることができます。 。

#注意VI需要延后一个使用
df['price_change'] = np.log(df['price']/df['price'].rolling(40).mean())
df['CI'] = -1.5*df['VI'].shift()+0.7*(0.7*df['I']+0.2*df['I_2']+0.1*df['I_3'])**3 + 150*df['price_change'].shift(1)

df['adjust_mid_price_11'] = df['mid_price'] + df['spread']*(df['CI'])
print('调整后的mid_price_11的误差：', ((df['price']-df['adjust_mid_price_11'])**2).sum())

调整后的mid_price_11的误差： 0.00421125960463469

要約する

本論文では、深度データと取引データを組み合わせて仲値の計算方法をさらに改善し、精度を測定する方法を提供し、価格変動予測の精度を向上させます。全体的に、さまざまなパラメータはそれほど厳密ではなく、参考値としてのみ使用されます。より正確な仲値が得られたら、次は実際に仲値を適用してバックテストを行っていきます。この部分も内容が多いので、しばらく更新を中止します。