この記事では、デイトレード戦略について説明します。 「平均回帰取引ペア」という古典的な取引概念を使用します。この例では、ニューヨーク証券取引所 (NYSE) で取引され、米国の株式市場指数である S&P 500 とラッセル 2000 を表す 2 つの上場投資信託 (ETF)、SPY と IWM を利用します。” 。

この戦略では、1 つの ETF を買い、別の ETF を売り、キャリーを作成します。ロングショート比率は、統計的共和分時系列法を使用するなど、さまざまな方法で定義できます。このシナリオでは、ローリング線形回帰を使用して SPY と IWM 間のヘッジ比率を計算します。これにより、Z スコアに正規化された SPY と IWM 間の「スプレッド」を作成できます。 Z スコアが特定のしきい値を超えると、この「スプレッド」が平均値に戻ると考えられるため、取引シグナルが生成されます。

この戦略の根拠は、SPY と IWM の両方がほぼ同じ市場シナリオ、つまり米国の大企業と中小企業のグループの株価動向を表しているという点です。前提は、価格の「平均回帰」理論を受け入れると、価格は常に回帰するということであり、「イベント」はS&P500とラッセル2000に非常に短期間で別々に影響を与える可能性があるが、両者の「金利差」はこれらは常に通常の平均値に戻り、2 つの長期価格系列は常に共和分化されます。

戦略

戦略は次のように実行されます。

データ - 2007 年 4 月から 2014 年 2 月までの SPY と IWM の 1 分足ローソク足チャートを取得します。

処理 - データを正しく整列させ、互いに欠落しているバーを削除します。 （片側が欠けている場合は両側とも削除されます）

スプレッド - 2 つの ETF 間のヘッジ比率は、ローリング線形回帰を使用して計算されます。 1 バー分前進するルックバック ウィンドウを使用してベータ回帰係数として定義され、回帰係数が再計算されます。したがって、ヘッジ比率 βi、bi K ラインは、bi-1-k から bi-1 への交差点を計算することによって K ラインをトレースするために使用されます。

Z スコア - 標準スプレッドの値は通常の方法で計算されます。これは、スプレッド（サンプル）の平均を減算し、スプレッド（サンプル）の標準偏差で割ることを意味します。これを行う理由は、Z スコアが無次元量であるため、しきい値パラメータを理解しやすくするためです。私は、それがいかに微妙であるかを示すために、意図的に「先読みバイアス」を計算に導入しました。ぜひお試しください！

取引 - 負の Z スコア値が所定の (または最適化後の) しきい値を下回るとロング シグナルが生成され、その逆の場合はショート シグナルが生成されます。 Z スコアの絶対値が追加のしきい値を下回ると、ポジションをクローズするシグナルが生成されます。この戦略では、（多少恣意的に）エントリしきい値として |z| = 2 を選択し、終了しきい値として |z| = 1 を選択しました。平均回帰がスプレッドに影響を与えると仮定すると、上記はうまくいけばこの裁定関係を捉え、大きな利益をもたらすでしょう。

おそらく、戦略を深く理解する最良の方法は、実際にそれを実行することです。次のセクションでは、この平均回帰戦略を実装するために使用される完全な Python コード (単一ファイル) について詳しく説明します。理解を深めるために詳細なコードコメントを追加しました。

Python実装

すべての Python/pandas チュートリアルと同様に、このチュートリアルで説明されているように Python 環境を設定する必要があります。セットアップが完了したら、最初のタスクは必要な Python ライブラリをインポートすることです。これは、matplotlib と pandas を使用するために必要です。

私が使用している具体的なライブラリのバージョンは次のとおりです。

Python - 2.7.3 NumPy - 1.8.0 pandas - 0.12.0 matplotlib - 1.1.0

では、これらのライブラリをインポートしてみましょう。

# mr_spy_iwm.py

import matplotlib.pyplot as plt
import numpy as np
import os, os.path
import pandas as pd

次の関数 create_pairs_dataframe は、2 つのシンボルの日中ローソク足を含む 2 つの CSV ファイルをインポートします。私たちの場合、これは SPY と IWM になります。次に、元の両方のファイルのインデックスを使用する別の「データ フレームのペア」を作成します。トランザクションの欠落やエラーにより、タイムスタンプが異なる場合があります。これは、pandas のようなデータ分析ライブラリを使用する主な利点の 1 つです。私たちは「定型」コードを非常に効率的に処理します。

# mr_spy_iwm.py
def create_pairs_dataframe(datadir, symbols):
    """Creates a pandas DataFrame containing the closing price
    of a pair of symbols based on CSV files containing a datetime
    stamp and OHLCV data."""
 
    # Open the individual CSV files and read into pandas DataFrames
    print "Importing CSV data..."
    sym1 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[0]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
    sym2 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[1]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
 
    # Create a pandas DataFrame with the close prices of each symbol
    # correctly aligned and dropping missing entries
    print "Constructing dual matrix for %s and %s..." % symbols    
    pairs = pd.DataFrame(index=sym1.index)
    pairs['%s_close' % symbols[0].lower()] = sym1['close']
    pairs['%s_close' % symbols[1].lower()] = sym2['close']
    pairs = pairs.dropna()
    return pairs

次のステップは、SPY と IWM の間でローリング線形回帰を実行することです。このシナリオでは、IWM が予測子 (‘x’) であり、SPY が応答 (‘y’) です。デフォルトのルックバックウィンドウを 100 本のローソク足に設定しました。上で述べたように、これらは戦略のパラメータです。戦略が堅牢であるとみなされるためには、理想的には、ルックバック期間にわたって凸状のリターン レポート (またはその他のパフォーマンス測定基準) を確認する必要があります。したがって、コードの後の段階で、スコープ内のルックバック期間を変更して感度分析を実行します。

SPY-IWM の線形回帰モデルでローリング ベータ係数を計算した後、それを DataFrame ペアに追加し、空の行を削除します。これにより、ルックバック長のトリミングされた測定値に等しい最初のローソク足セットが構築されます。次に、2 つの ETF 間にスプレッド (SPY 1 ユニットと IWM -βi 1 ユニット) を作成しました。明らかに、これは現実的なシナリオではありません。少量の IWM を採用しているため、実際の実装では不可能です。

最後に、スプレッドの平均を減算し、スプレッドの標準偏差で正規化して計算されたスプレッドの Z スコアを作成します。ここでは、かなり微妙な「将来志向のバイアス」が働いていることに注意することが重要です。研究においてこのような間違いがいかに簡単に起こるかを強調したかったので、意図的にコード内に残しました。スプレッド時系列全体の平均と標準偏差を計算します。これが真の歴史的正確さを反映することを意図している場合、この情報は暗黙的に未来からの情報を利用するため、取得できません。したがって、Z スコアを計算するには、ローリング平均と標準偏差を使用する必要があります。

# mr_spy_iwm.py
 
def calculate_spread_zscore(pairs, symbols, lookback=100):
    """Creates a hedge ratio between the two symbols by calculating
    a rolling linear regression with a defined lookback period. This
    is then used to create a z-score of the 'spread' between the two
    symbols based on a linear combination of the two."""
     
    # Use the pandas Ordinary Least Squares method to fit a rolling
    # linear regression between the two closing price time series
    print "Fitting the rolling Linear Regression..."
    model = pd.ols(y=pairs['%s_close' % symbols[0].lower()], 
                   x=pairs['%s_close' % symbols[1].lower()],
                   window=lookback)
 
    # Construct the hedge ratio and eliminate the first 
    # lookback-length empty/NaN period
    pairs['hedge_ratio'] = model.beta['x']
    pairs = pairs.dropna()
 
    # Create the spread and then a z-score of the spread
    print "Creating the spread/zscore columns..."
    pairs['spread'] = pairs['spy_close'] - pairs['hedge_ratio']*pairs['iwm_close']
    pairs['zscore'] = (pairs['spread'] - np.mean(pairs['spread']))/np.std(pairs['spread'])
    return pairs

create_long_short_market_signals で、取引シグナルを作成します。これらは、しきい値を超える Z スコア値を測定することによって計算されます。 Z スコアの絶対値が別の（より小さい）しきい値以下の場合、ポジションをクローズするシグナルが発行されます。

これを実現するには、各 K ラインの取引戦略が「オープン」か「クローズ」かを確立する必要があります。 Long_market と short_market は、ロングポジションとショートポジションを追跡するために定義された 2 つの変数です。残念ながら、ベクトル化されたアプローチよりも反復的な方法でプログラミングする方がはるかに簡単なので、計算速度が遅くなります。 1 分間のローソク足チャートには CSV ファイルごとに約 700,000 のデータ ポイントが必要ですが、それでも古いデスクトップで計算するのは比較的簡単です。

pandas DataFrame を反復処理するには (確かに珍しい操作ですが)、反復可能なジェネレーターを提供する iterrows メソッドを使用する必要があります。

# mr_spy_iwm.py
 
def create_long_short_market_signals(pairs, symbols, 
                                     z_entry_threshold=2.0, 
                                     z_exit_threshold=1.0):
    """Create the entry/exit signals based on the exceeding of 
    z_enter_threshold for entering a position and falling below
    z_exit_threshold for exiting a position."""
 
    # Calculate when to be long, short and when to exit
    pairs['longs'] = (pairs['zscore'] <= -z_entry_threshold)*1.0
    pairs['shorts'] = (pairs['zscore'] >= z_entry_threshold)*1.0
    pairs['exits'] = (np.abs(pairs['zscore']) <= z_exit_threshold)*1.0
 
    # These signals are needed because we need to propagate a
    # position forward, i.e. we need to stay long if the zscore
    # threshold is less than z_entry_threshold by still greater
    # than z_exit_threshold, and vice versa for shorts.
    pairs['long_market'] = 0.0
    pairs['short_market'] = 0.0
 
    # These variables track whether to be long or short while
    # iterating through the bars
    long_market = 0
    short_market = 0
 
    # Calculates when to actually be "in" the market, i.e. to have a
    # long or short position, as well as when not to be.
    # Since this is using iterrows to loop over a dataframe, it will
    # be significantly less efficient than a vectorised operation,
    # i.e. slow!
    print "Calculating when to be in the market (long and short)..."
    for i, b in enumerate(pairs.iterrows()):
        # Calculate longs
        if b[1]['longs'] == 1.0:
            long_market = 1            
        # Calculate shorts
        if b[1]['shorts'] == 1.0:
            short_market = 1
        # Calculate exists
        if b[1]['exits'] == 1.0:
            long_market = 0
            short_market = 0
        # This directly assigns a 1 or 0 to the long_market/short_market
        # columns, such that the strategy knows when to actually stay in!
        pairs.ix[i]['long_market'] = long_market
        pairs.ix[i]['short_market'] = short_market
    return pairs

この段階では、実際のロングとショートのシグナルが含まれるようにペアを更新し、ポジションを開く必要があるかどうかを判断できます。ここで、ポジションの市場価値を追跡するためのポートフォリオを作成する必要があります。最初のタスクは、ロング信号とショート信号を組み合わせたポジション列を作成することです。これには (1,0,-1) の要素のリストが含まれます。ここで、1 はロング ポジション、0 はポジションなし (クローズする必要があります)、-1 はショート ポジションを表します。 sym1 列と sym2 列は、各ローソク足の終了時の SPY および IWM ポジションの市場価値を表します。

ETF の市場価値が作成されると、それらを合計して各ローソク足の終わりの合計市場価値が生成されます。その後、そのオブジェクトの pct_change メソッドを介して戻り値に変換されます。後続のコード行では、エラーのあるエントリ (NaN および inf 要素) をクリーンアップし、最終的に完全なエクイティ カーブを計算します。

# mr_spy_iwm.py
 
def create_portfolio_returns(pairs, symbols):
    """Creates a portfolio pandas DataFrame which keeps track of
    the account equity and ultimately generates an equity curve.
    This can be used to generate drawdown and risk/reward ratios."""
     
    # Convenience variables for symbols
    sym1 = symbols[0].lower()
    sym2 = symbols[1].lower()
 
    # Construct the portfolio object with positions information
    # Note that minuses to keep track of shorts!
    print "Constructing a portfolio..."
    portfolio = pd.DataFrame(index=pairs.index)
    portfolio['positions'] = pairs['long_market'] - pairs['short_market']
    portfolio[sym1] = -1.0 * pairs['%s_close' % sym1] * portfolio['positions']
    portfolio[sym2] = pairs['%s_close' % sym2] * portfolio['positions']
    portfolio['total'] = portfolio[sym1] + portfolio[sym2]
 
    # Construct a percentage returns stream and eliminate all 
    # of the NaN and -inf/+inf cells
    print "Constructing the equity curve..."
    portfolio['returns'] = portfolio['total'].pct_change()
    portfolio['returns'].fillna(0.0, inplace=True)
    portfolio['returns'].replace([np.inf, -np.inf], 0.0, inplace=True)
    portfolio['returns'].replace(-1.0, 0.0, inplace=True)
 
    # Calculate the full equity curve
    portfolio['returns'] = (portfolio['returns'] + 1.0).cumprod()
    return portfolio

メイン関数はこれらすべてを結び付けます。日中 CSV ファイルは、datadir パスにあります。必ず次のコードを変更して、特定のディレクトリを指すようにしてください。

戦略がルックバック期間に対してどの程度敏感であるかを判断するには、ルックバック パフォーマンス メトリックの範囲を計算する必要があります。パフォーマンス指標としてポートフォリオの最終的な総収益率を選択し、ルックバック範囲を選択しました。[50,200] まで増加し、10 ずつ増加します。以下のコードを見ると、前の関数がこの範囲で for ループにラップされており、他のしきい値は同じままであることがわかります。最後のタスクは、matplotlib を使用してルックバックとリターンの折れ線グラフを作成することです。

# mr_spy_iwm.py
 
if __name__ == "__main__":
    datadir = '/your/path/to/data/'  # Change this to reflect your data path!
    symbols = ('SPY', 'IWM')
 
    lookbacks = range(50, 210, 10)
    returns = []
 
    # Adjust lookback period from 50 to 200 in increments
    # of 10 in order to produce sensitivities
    for lb in lookbacks: 
        print "Calculating lookback=%s..." % lb
        pairs = create_pairs_dataframe(datadir, symbols)
        pairs = calculate_spread_zscore(pairs, symbols, lookback=lb)
        pairs = create_long_short_market_signals(pairs, symbols, 
                                                z_entry_threshold=2.0, 
                                                z_exit_threshold=1.0)
 
        portfolio = create_portfolio_returns(pairs, symbols)
        returns.append(portfolio.ix[-1]['returns'])
 
    print "Plot the lookback-performance scatterchart..."
    plt.plot(lookbacks, returns, '-o')
    plt.show()

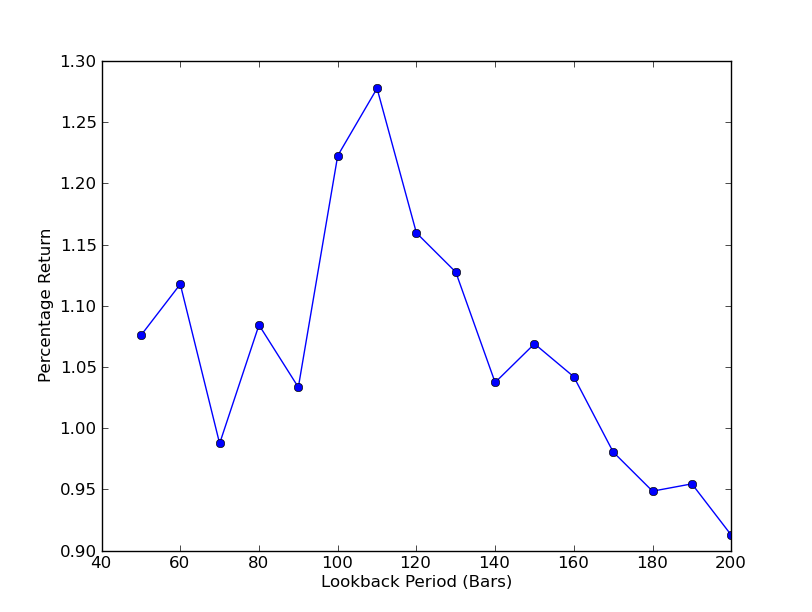
これで、ルックバックとリターンのグラフが表示されます。ルックバックには「グローバル」最大値があり、110 バーに相当することに注意してください。ルックバックがリターンと何の関係もない状況が見られる場合、その理由は次の通りです。

SPY-IWM線形回帰ヘッジ比率ルックバック期間感度分析

上向きの利益曲線がなければ、バックテストの記事は完成しません。したがって、累積利益率を時間に対してプロットする場合は、次のコードを使用できます。ルックバックパラメータスタディから生成された最終ポートフォリオをプロットします。したがって、視覚化したいチャートに応じてルックバックを選択する必要があります。このグラフでは、比較しやすいように、同じ期間の SPY の収益もプロットしています。

# mr_spy_iwm.py
 
    # This is still within the main function
    print "Plotting the performance charts..."
    fig = plt.figure()
    fig.patch.set_facecolor('white')
 
    ax1 = fig.add_subplot(211,  ylabel='%s growth (%%)' % symbols[0])
    (pairs['%s_close' % symbols[0].lower()].pct_change()+1.0).cumprod().plot(ax=ax1, color='r', lw=2.)
 
    ax2 = fig.add_subplot(212, ylabel='Portfolio value growth (%%)')
    portfolio['returns'].plot(ax=ax2, lw=2.)
 
    fig.show()

次の株式曲線チャートのルックバック期間は 100 日です。

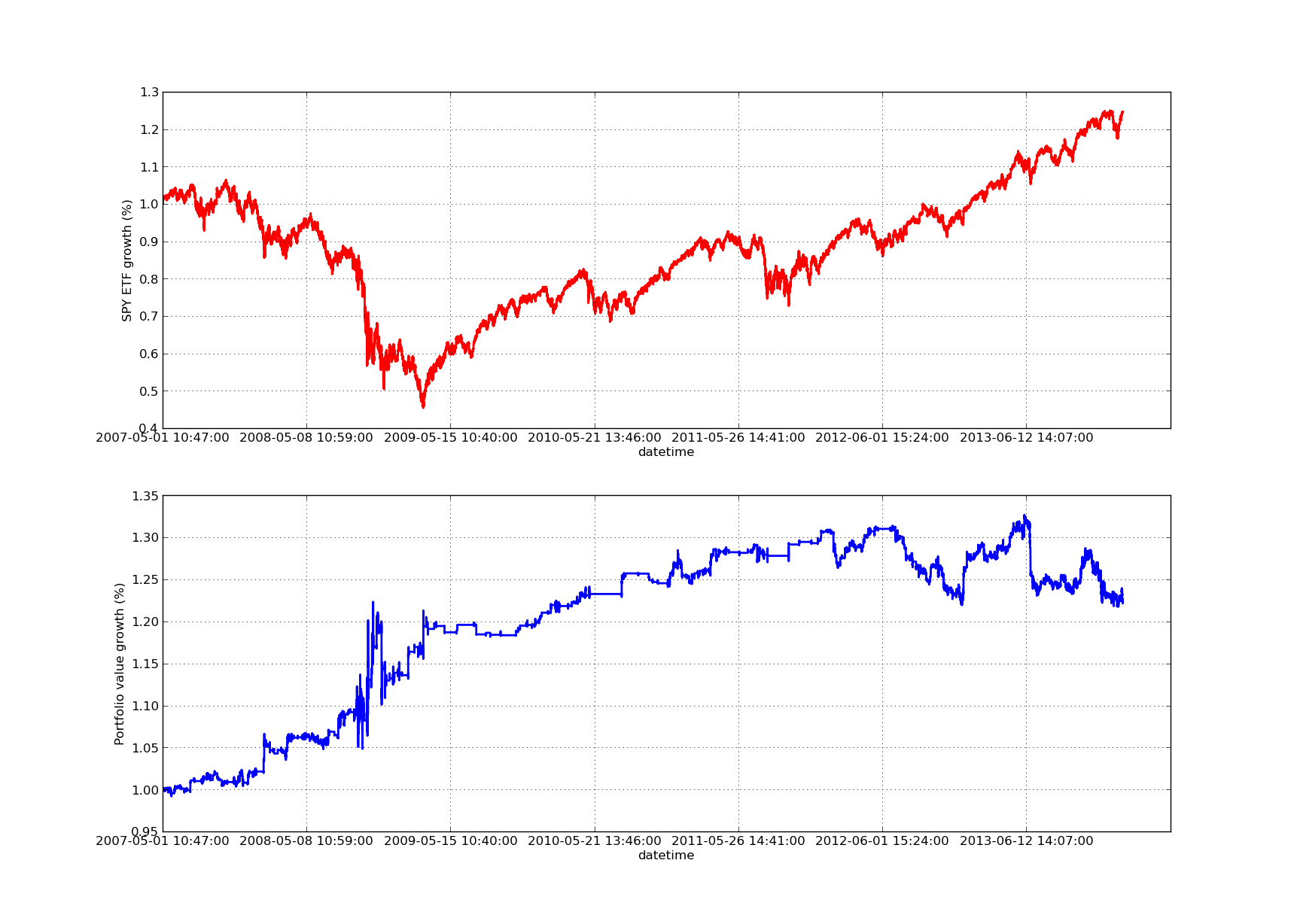
SPY-IWM線形回帰ヘッジ比率ルックバック期間感度分析

2009 年の金融危機の際の SPY の下落はかなり大きかったことに注意してください。このフェーズでは、戦略も混乱期にあります。また、この期間中の SPY の強いトレンド特性が S&P 500 を反映しているため、パフォーマンスは過去 1 年間で悪化していることにも注意してください。

Z スコアの広がりを計算する際には、「先読みバイアス」を考慮する必要があることに注意してください。さらに、これらの計算はすべて取引コストなしで実行されます。これらの要素を考慮すると、この戦略のパフォーマンスは必ず悪くなります。手数料とスリッページはどちらも現時点では未定です。さらに、この戦略では ETF の小数単位で取引しますが、これも非常に非現実的です。

今後の記事では、上記のすべてを考慮した、より複雑なイベント駆動型バックテスターを作成し、エクイティ カーブとパフォーマンス指標に対する信頼性を高めます。