AR-GARCH時系列予測戦略
複雑な市場では,なぜ従来の技術分析がうまくいかないのか?
量的な取引では,なぜ単純な移動平均またはRSIに基づく戦略が特定の市場環境で優れているのに,他の市場環境では頻繁に失敗するのかという疑問がよく浮かびます. 答えは,金融時間軸の複雑さにあります. それは自己関連性だけでなく,時折変動する波動率の特質もあります.
今日分析するこの戦略は,巧妙にAR(2) 自帰帰モデルとGARCH(1,1) 条件差異モデルを組み合わせて,この問題を統計学的観点から解決しようとしています.これは,単なる技術指標の重複ではなく,金融時間序列の本質的な特性を深く掘り下げています.
価格の記憶効果をどのように捉えるのか?
戦略の核心はAR(2) 自帰模型の適用である.自帰とは?簡潔に言えば,過去の自己を使って将来の自己を予測することである.AR(2) モデルでは,現在の利回りは,前2期の利回り率によって線形的に表現できると仮定している.
r_t = φ₁ × r_{t-1} + φ₂ × r_{t-2} + ε_t
このコードでは,ユール=ウォーカー方程式でφ1とφ2の因数分解:
c0 = calcAutoCovariance(returns, 0, lengthReg) // 滞后0期自协方差
c1 = calcAutoCovariance(returns, 1, lengthReg) // 滞后1期自协方差
c2 = calcAutoCovariance(returns, 2, lengthReg) // 滞后2期自协方差
phi1 = (c1 * c0 - c2 * c1) / denominator // 第一个自回归系数
phi2 = (c2 * c0 - c1 * c1) / denominator // 第二个自回归系数
この方法の利点は,主観的な判断を頼らずに,データ自体が”話す”ことで,価格の配列に隠された規則性を発見することです.
GARCHモデルが市場リスクを より良く描写できるのはなぜか?
ARモデルだけでは不十分です. 金融市場の変動率は恒定ではないからです. 大幅な波動が大きな波動に伴い,静寂期が長く続くことが多いのは”波動率の集まる”現象です.
GARCH ((1,1) モデルはまさにこの特性を描くためのものです.
σ²_t = ω + α × ε²_{t-1} + β × σ²_{t-1}
プログラミングにおける実装ロジックは,このことを明確に示しています.
omega = (1 - adjustedAlpha - adjustedBeta) * longTermVar
garchVariance := omega + adjustedAlpha * math.pow(arResidual[1], 2) + adjustedBeta * garchVariance[1]
ここでの重要な洞察は,現在の条件差は,前期残差の二乗 ((短期的衝撃)) に依存するだけでなく,前期条件差 ((長期的持続性)) にも依存するということです.パラメータαは短期的衝撃の影響を制御し,βは波動率の持続性を制御します.
戦略の取引論理は,どのようにリスクと利益のバランスをとるのか?
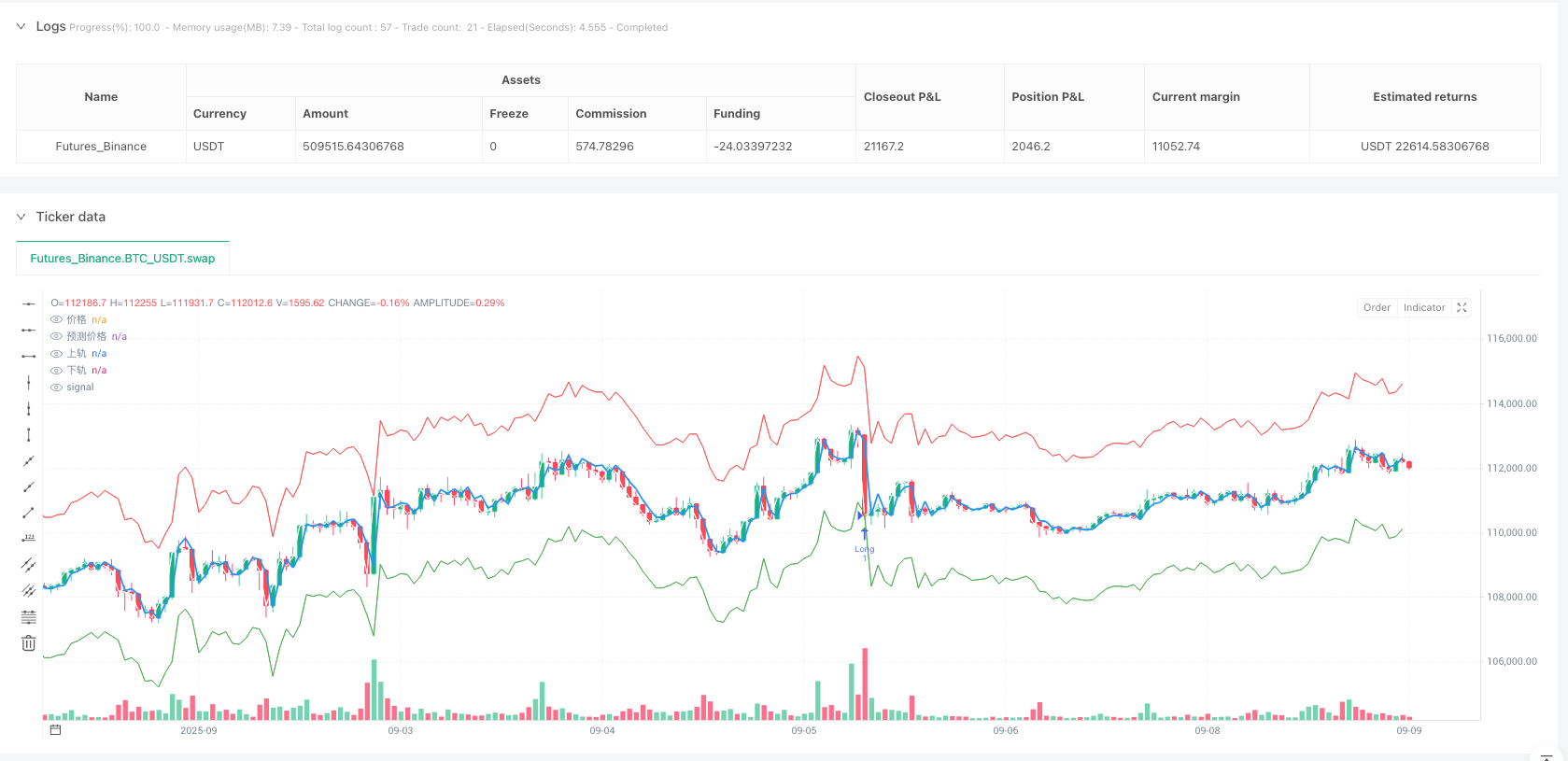
AR予測とGARCH変動率の推定により,戦略は動的な信頼区間を構築した.
upperReturnBand = arReturnPredict + stdevFactor * garchStd
lowerReturnBand = arReturnPredict - stdevFactor * garchStd
取引シグナルの生成ロジックは平均値帰帰帰の思想を体現している.
- 価格が下がったときに多めにします.
- 価格が上線を突破したときに空白を空白する.
このデザインの巧妙な点は,信頼区間の幅が市場の変動率の動向に合わせて調整されるという点にある.高波動期には,区間が広くなり,取引頻度が減る;低波動期には,区間が狭くなり,取引機会が増加する.
具体的には,どのような重要な問題に取り組むべきか?
1. モデル安定性テスト このコードには重要な安定性チェックが含まれています.
if stabilityCheck >= 0.99 or math.abs(phi2) >= 0.99
scaleFactor = 0.95 / math.max(stabilityCheck, math.abs(phi2) + 0.01)
これはARモデルの安定性を確保し,散らばった予測結果を回避する.
2. 参数収束制 GARCHモデルは,α + β < 1 を要求し,長期差の存在を保証する.
if sumParam >= 0.999
scale = 0.99 / sumParam
3. フィルタリングの必要性 策略はRSIフィルタリングオプションを提供しており,これは実用的なアプリケーションで重要です.純粋な統計モデルでは市場の傾向特性が無視され,技術指標の加入は追加の確認信号を提供することができます.
戦略の限界と改善の方向
この戦略は理論上は優雅ですが,実際は以下のようなことを考慮する必要があります.
データ周波数の選択:AR-GARCHモデルは,異なる周期下でのパフォーマンスは大きく異なっています.高周波データにより,より多くの情報を提供できますが,より多くのノイズも導入できます.
パラメータの時間変性: 現行では,ARとGARCHのパラメータが推定ウィンドウで一定であると仮定しているが,実際の市場構造は変化する可能性がある.
取引コストの影響統計的に見ると,値策には通常,取引頻度が高く,手数料やスライドポイントコストは無視できない.
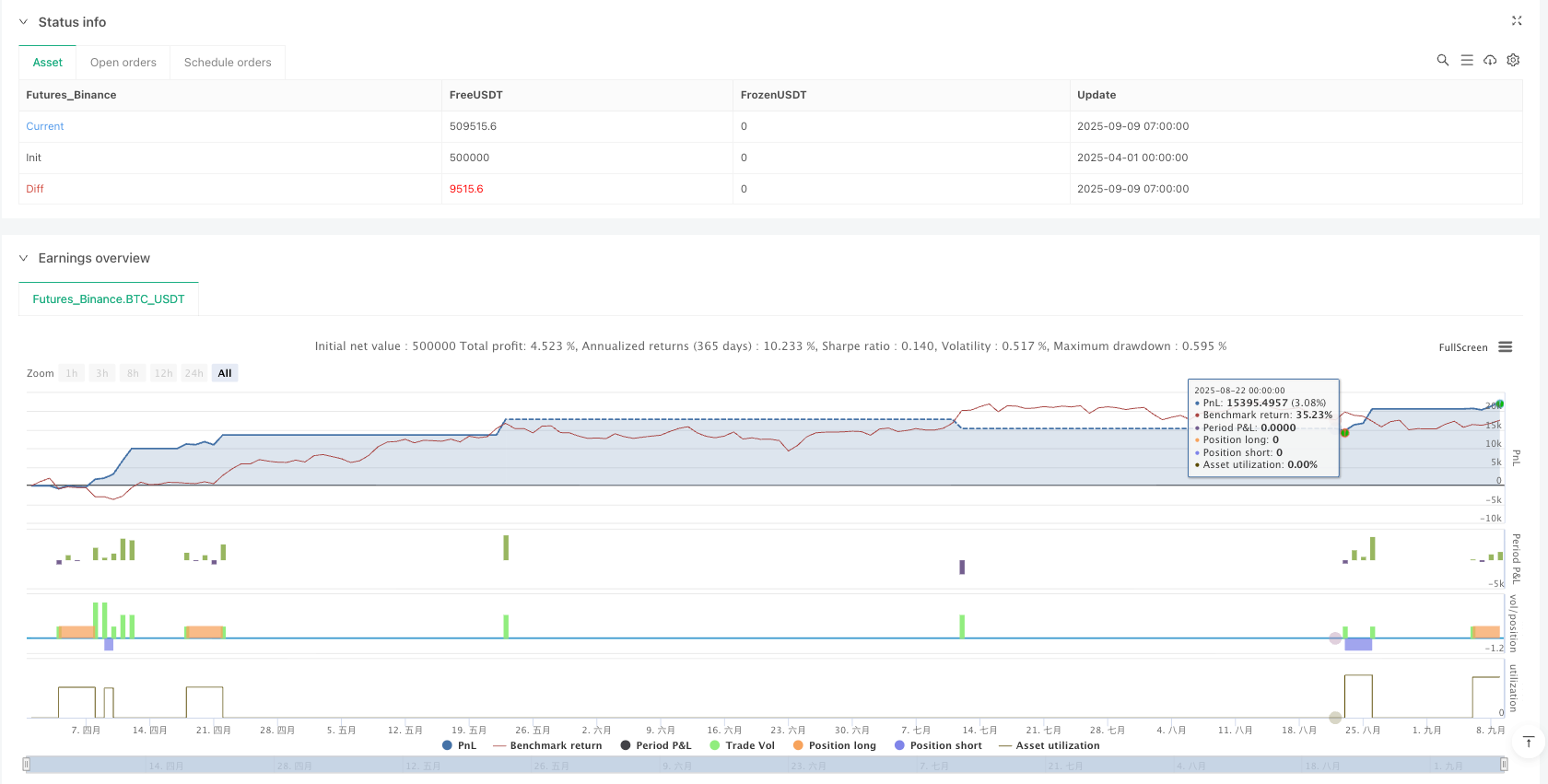
結論: 統計モデリングの価値は 量的な取引において
このAR-GARCH戦略は,金融モデリングにおける近代的な統計学の強力な力を示しています.それは,単なる技術指標の組み合わせではなく,金融のタイムシーケンスの統計学的特性を深く掘り下げています.
量的なトレーダーにとって,このような戦略を理解する価値は,直接の応用だけでなく,市場を統計的思考で分析する能力を育むことにある. AIと機械学習が普及している今日,これらの古典的な統計モデルは,市場を理解し,戦略を構築する上で重要な基石です.
/*backtest
start: 2025-04-01 00:00:00
end: 2025-09-09 08:00:00
period: 1h
basePeriod: 1h
exchanges: [{"eid":"Futures_Binance","currency":"BTC_USDT","balance":500000}]
*/
//@version=5
strategy("AR(2)-GARCH Strategy", overlay=true)
//策略参数设置:配置AR模型、GARCH模型和交易信号的各项参数
lengthReg = input.int(50, "AR估计窗口", minval=50, maxval=200);//AR模型回归窗口长度
//GARCH波动率模型参数:控制条件方差的计算
useGarch = input.bool(true, "启用GARCH波动率");//是否启用GARCH波动率建模
garchAlpha = input.float(0.1, "GARCH Alpha", minval=0.01, maxval=0.3, step=0.01);//GARCH模型alpha参数
garchBeta = input.float(0.85, "GARCH Beta", minval=0.5, maxval=0.95, step=0.01);//GARCH模型beta参数
//交易信号生成参数:控制买卖信号的敏感度
stdevFactor = input.float(2.0, "标准差倍数", minval=1.0, maxval=3.0, step=0.1);//交易波段的标准差倍数
//风险控制参数:设置止损止盈水平
stopLossPerc = input.float(2.0, "止损 (%)", minval=0.5, maxval=5.0, step=0.1);//止损百分比
takeProfitPerc = input.float(4.0, "止盈 (%)", minval=1.0, maxval=10.0, step=0.1);//止盈百分比
//RSI过滤器参数:添加技术指标过滤条件
useRsiFilter = input.bool(false, "启用RSI过滤");//是否启用RSI过滤器
rsiLen = input.int(14, "RSI周期", minval=7, maxval=21);//RSI指标计算周期
rsiOB = input.float(70, "RSI超买线", minval=60, maxval=80);//RSI超买阈值
rsiOS = input.float(30, "RSI超卖线", minval=20, maxval=40);//RSI超卖阈值
//数据预处理:计算收益率序列
rawPrice = close;//原始收盘价
returns = math.log(rawPrice / rawPrice[1]);//对数收益率序列
//获取滞后收益率数据:AR(2)模型需要前两期的收益率数据
returns1 = returns[1];//滞后1期的收益率
returns2 = returns[2];//滞后2期的收益率
//计算收益率序列的移动平均值:作为AR模型的均值项
returnsMean = ta.sma(returns, lengthReg);//收益率的简单移动平均
//AR(2)模型系数计算:使用Yule-Walker方程求解自回归系数
//自协方差函数计算:计算不同滞后期的自协方差
calcAutoCovariance(data, lag, length) =>
mean = ta.sma(data, length);//计算数据的均值
sum = 0.0;//协方差累计值
count = 0;//有效数据点计数
for i = lag to length - 1
if not na(data[i]) and not na(data[i-lag])
sum := sum + (data[i] - mean) * (data[i-lag] - mean);//计算协方差分子
count := count + 1;//累计有效数据点
count > 0 ? sum / count : 0.0;//返回协方差值
//计算AR(2)模型所需的自协方差:用于Yule-Walker方程
c0 = calcAutoCovariance(returns, 0, lengthReg);//滞后0期的自协方差(即方差)
c1 = calcAutoCovariance(returns, 1, lengthReg);//滞后1期的自协方差
c2 = calcAutoCovariance(returns, 2, lengthReg);//滞后2期的自协方差
//Yule-Walker方程求解:计算AR(2)模型的两个自回归系数
// φ₁ = (c₁c₀ - c₂c₁) / (c₀² - c₁²)
// φ₂ = (c₂c₀ - c₁²) / (c₀² - c₁²)
denominator = c0 * c0 - c1 * c1;//分母计算
phi1 = denominator != 0 ? (c1 * c0 - c2 * c1) / denominator : 0.0;//第一个自回归系数
phi2 = denominator != 0 ? (c2 * c0 - c1 * c1) / denominator : 0.0;//第二个自回归系数
//AR(2)稳定性检验:确保模型稳定性条件 |φ₁| + |φ₂| < 1 且 |φ₂| < 1
stabilityCheck = math.abs(phi1) + math.abs(phi2);//计算系数绝对值之和
if stabilityCheck >= 0.99 or math.abs(phi2) >= 0.99
scaleFactor = 0.95 / math.max(stabilityCheck, math.abs(phi2) + 0.01);//计算缩放因子
phi1 := phi1 * scaleFactor;//调整第一个系数
phi2 := phi2 * scaleFactor;//调整第二个系数
//AR(2)收益率预测:根据历史收益率和AR系数预测下一期收益率
arReturnPredict = returnsMean + phi1 * (returns1 - returnsMean) + phi2 * (returns2 - returnsMean);//AR(2)预测公式
//计算AR模型的预测残差:用于GARCH建模
arResidual = returns - arReturnPredict;//AR模型的预测残差
//GARCH(1,1)波动率建模:对AR残差进行条件方差建模
var float garchVariance = na;//GARCH方差变量
var float longTermVar = na;//长期方差变量
//长期方差初始化:使用历史残差计算初始方差值
if na(longTermVar) and bar_index > lengthReg
longTermVar := ta.variance(arResidual, lengthReg);//计算长期方差
//GARCH参数调整:确保参数满足收敛条件
adjustedAlpha = garchAlpha;//调整后的alpha参数
adjustedBeta = garchBeta;//调整后的beta参数
sumParam = garchAlpha + garchBeta;//参数和
if sumParam >= 0.999
scale = 0.99 / sumParam;//计算参数缩放比例
adjustedAlpha := garchAlpha * scale;//调整alpha参数
adjustedBeta := garchBeta * scale;//调整beta参数
//GARCH(1,1)递归更新:根据GARCH公式更新条件方差
if useGarch and not na(longTermVar) and not na(arResidual)
if na(garchVariance)
garchVariance := longTermVar;//初始化GARCH方差
else
omega = (1 - adjustedAlpha - adjustedBeta) * longTermVar;//GARCH常数项
garchVariance := omega + adjustedAlpha * math.pow(arResidual[1], 2) + adjustedBeta * garchVariance[1];//GARCH递归公式
//条件标准差计算:从条件方差计算标准差
garchStd = useGarch and not na(garchVariance) ? math.sqrt(math.max(garchVariance, 0.0001)) : ta.stdev(arResidual, 20);//启用GARCH时使用条件标准差,否则使用历史标准差
//收益率空间的置信区间构建:基于AR预测和GARCH波动率
upperReturnBand = arReturnPredict + stdevFactor * garchStd;//上轨:预测收益率加上标准差倍数
lowerReturnBand = arReturnPredict - stdevFactor * garchStd;//下轨:预测收益率减去标准差倍数
//将置信区间转换为价格空间:用于实际交易信号生成
//基于预测收益率计算预测价格
predictedPrice = rawPrice[1] * math.exp(arReturnPredict);//根据预测收益率计算预测价格
upperPriceBand = rawPrice[1] * math.exp(upperReturnBand);//上轨价格
lowerPriceBand = rawPrice[1] * math.exp(lowerReturnBand);//下轨价格
//交易信号生成:基于当前价格相对于置信区间的位置
longSignal = rawPrice < lowerPriceBand;//做多信号:当前价格低于下轨
shortSignal = rawPrice > upperPriceBand;//做空信号:当前价格高于上轨
//RSI过滤器:使用RSI指标过滤交易信号
if useRsiFilter
rsi = ta.rsi(rawPrice, rsiLen);//计算RSI指标
longSignal := longSignal and rsi < rsiOS;//做多信号需要RSI超卖确认
shortSignal := shortSignal and rsi > rsiOB;//做空信号需要RSI超买确认
//策略执行:根据交易信号开仓和平仓
//开仓操作:根据信号建立多头或空头仓位
if longSignal
strategy.entry("Long", strategy.long);//开多仓
if shortSignal
strategy.entry("Short", strategy.short);//开空仓
//风险控制:设置止损止盈条件
if strategy.position_size > 0
strategy.exit("Long Exit", "Long",
stop=strategy.position_avg_price * (1 - stopLossPerc/100),
limit=strategy.position_avg_price * (1 + takeProfitPerc/100));//多仓止损止盈
if strategy.position_size < 0
strategy.exit("Short Exit", "Short",
stop=strategy.position_avg_price * (1 + stopLossPerc/100),
limit=strategy.position_avg_price * (1 - takeProfitPerc/100));//空仓止损止盈
//图表显示:在图表上绘制价格、预测线和交易信号
//主要价格线和预测线:显示实际价格和基于收益率预测的价格
plot(rawPrice, color=color.white, linewidth=1, title="价格");//绘制实际价格线
plot(predictedPrice, color=color.blue, linewidth=2, title="预测价格");//绘制预测价格线
plot(upperPriceBand, color=color.red, linewidth=1, title="上轨");//绘制上轨线
plot(lowerPriceBand, color=color.green, linewidth=1, title="下轨");//绘制下轨线
//交易信号标记:在图表上标记买卖信号点
plotshape(longSignal, style=shape.triangleup, location=location.belowbar,
color=color.green, size=size.small, title="买入");//标记买入信号
plotshape(shortSignal, style=shape.triangledown, location=location.abovebar,
color=color.red, size=size.small, title="卖出");//标记卖出信号