SVM 벡터 머신으로 베팅(거래)을 하면 고릴라보다 빨리 달릴 수 있을까?

오늘 우리는 금융계에서 가장 무서운 경쟁자 중 하나로 여겨지는 오리랑을 물리치기 위해 최선을 다할 것입니다. 우리는 통화 거래 품종의 하루 뒤의 수익을 예측하려고 합니다. 나는 당신에게 확신합니다. 50%의 확률을 가지고 오리랑이를 이길 수 있는 것은 매우 어려운 일입니다. 우리는 기존의 머신러닝 알고리즘을 사용하여 벡터 분류기를 지원합니다. SVM 벡터 머신은 회귀와 분류 작업을 해결하는 데 매우 강력한 방법입니다.

• SVM 지원 벡터 기계

SVM 벡터 머신은 다음과 같은 아이디어에 기반합니다: 우리는 p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p

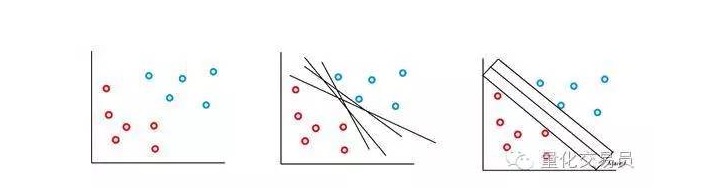
가장 간단한 경우, 선형 분류가 가능합니다. 알고리즘은 의사 결정 경계를 선택하여, 클래스 사이의 거리를 최대화 할 수 있습니다.

대부분의 금융 시시열에서 단순하고, 선형적으로 분리될 수 있는 집합은 거의 찾아볼 수 없지만, 분리되지 않는 집합은 자주 찾아볼 수 있다. SVM 벡터 기계는 소프트 마진 메소드 (soft margin method) 로 알려진 방법을 적용하여 이 문제를 해결했다.

이 경우, 일부 잘못된 분류가 허용되지만, C (비용 또는 예산의 오류가 허용될 수 있습니다) 와 직비례하는 인수와 오류의 경계까지의 거리를 최소화하기 위해 함수를 스스로 수행합니다.

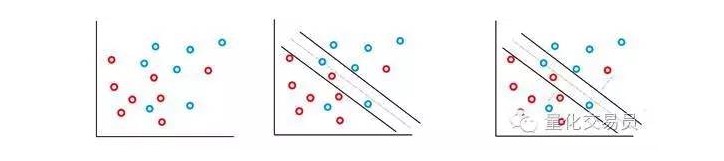
기본적으로, 기계는 분류 사이의 간격을 최대화하면서 C 가중된 처벌 항목을 최소화한다.

SVM 분류기는 분류 의사 결정 경계선의 위치와 크기가 의사 결정 경계선에서 가장 가까운 부분의 데이터에 의해서만 결정된다는 훌륭한 특징을 가지고 있다. 이 알고리즘의 특성으로 인해 멀리 떨어져 있는 비정상적인 값의 간섭에 대항할 수 있다. 예를 들어, 위의 그림에서 가장 오른쪽에 있는 파란색 점은 의사 결정 경계선에 거의 영향을 미치지 않는다.

너무 복잡하지 않나요? 음, 재미는 이제 막 시작됐다고 생각합니다.

다음의 경우를 고려해보세요:

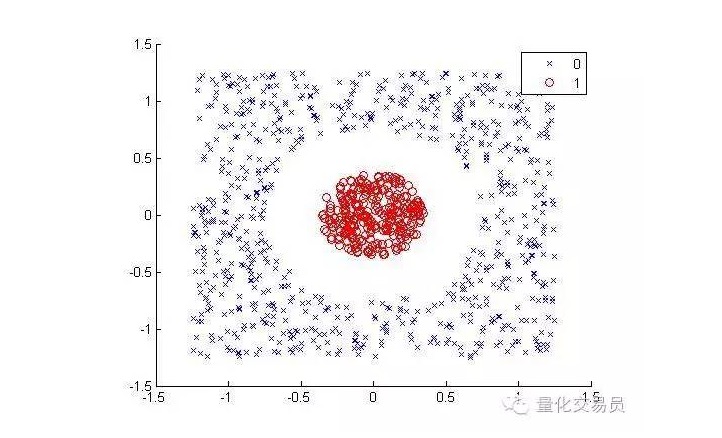
인간에게는 매우 간단하게 분류할 수 있다. 하지만 기계에게는 그렇지 않다. 명백히, 이것은 직선으로 만들 수 없다. 직선은 빨간 점을 분리할 수 없다. 여기서 우리는 ?? 内核技巧 ?? (kernel trick) 을 시도할 수 있다.

내핵 기법은 매우 똑똑한 수학 기술로, 우리가 (등급) 고차원 공간에서 선형적인 분류 문제를 풀 수 있게 해줍니다. 이제 어떻게 하는지 보겠습니다.

우리는 2차원 특징 공간을 3차원으로 변환하고, 분류가 끝나면 2차원으로 되돌릴 것입니다.

아래는 각자의 크기를 높여 지도화하고 분류한 후의 그림입니다.

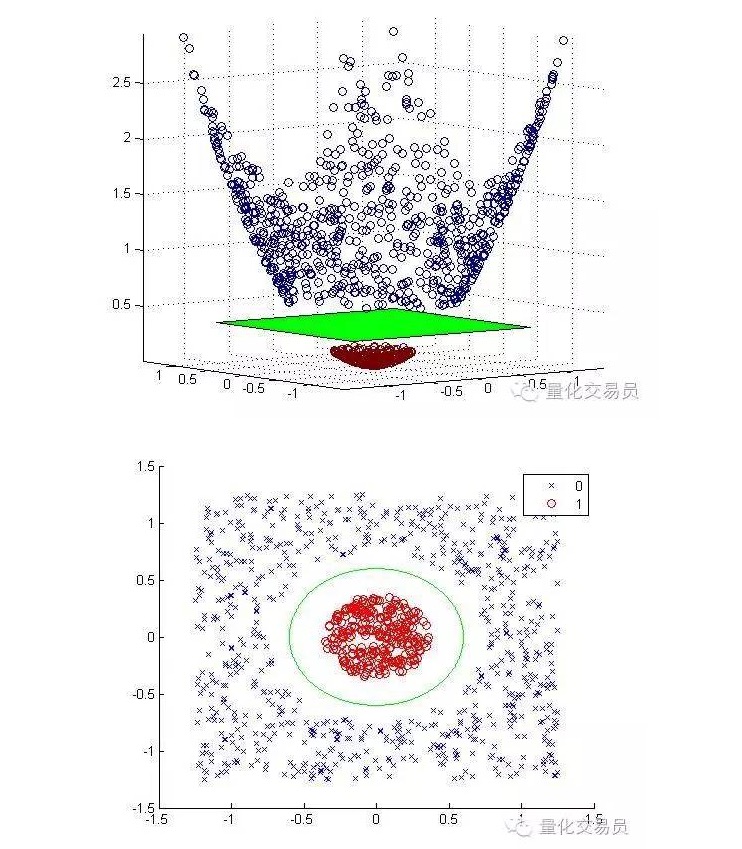
일반적으로, 만약 d개의 입력이 있다면, 당신은 d차원 입수 공간에서 p차원 특성 공간으로 하나의 맵핑을 사용할 수 있다. 위의 최소화 알고리즘이 생성하는 솔루션을 실행하고, 다시 당신의 원래 입수 공간의 p차원 초평면으로 맵핑한다.

위의 수학적 해결책의 중요한 전제는, 특징 공간에서 어떻게 좋은 점 샘플 세트를 생성하느냐에 달려 있다.

경계 최적화를 수행하기 위해 이러한 점 샘플 세트를 필요로 할 뿐이며, 맵핑은 명확하게 할 필요가 없으며, 입력 공간의 고차원 특성 공간의 점들은 핵 함수 ((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((

예를 들어, 여러분이 매우 큰 특징 공간에서 여러분의 분류 문제를 해결하려고 한다면, 100,000차원이라고 가정해 봅시다. 여러분이 필요로 하는 계산 능력을 상상할 수 있나요? 제가 여러분들이 그것을 할 수 있을지 매우 의심합니다. 좋습니다, 코어 (core) 는 이제 여러분이 이러한 점 샘플을 계산하도록 할 수 있습니다. 따라서, 이 엣지는 여러분이 낮은 농도에서 편안하게 입력하는 공간에서 나온 것입니다.

• 도전과 고리

이제 우리는 제프의 예측 능력을 물리칠 수 있는 도전을 준비하고 있습니다.

제프는 화폐 시장의 전문가로, 그는 50%의 예측 정확도를 얻을 수 있습니다. 이 정확도는 다음 거래 날의 수익률을 예측하는 신호입니다.

우리는 다양한 기본 시퀀스를 사용할 것입니다. 현금 가격 시퀀스, 각 시퀀스 최대 10 라그의 수익, 총 55 가지 특징.

우리가 만들려고 하는 SVM 벡터 기계는 3도 코어를 사용한다. 적절한 코어를 선택하는 것은 또 다른 매우 어려운 작업이라고 생각할 수 있다. C와 Γ의 파라미터를 교정하기 위해, 3배 크로스 검증은 가능한 파라미터 조합의 격자 위에 실행되며, 가장 좋은 그룹이 선택될 것이다.

하지만 그 결과는 그다지 고무적이지 않았습니다.

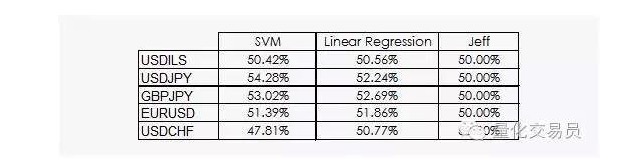
우리는 선형 회귀와 SVM 벡터 기계가 제프를 이길 수 있다는 것을 볼 수 있습니다. 결과는 낙관적이지 않지만, 우리는 데이터에서 정보를 얻을 수 있습니다. 이것은 이미 좋은 소식입니다. 왜냐하면 데이터 학문에서 금융 시간 순서는 매일의 이익이 아닙니다.

크로스 검증 후, 데이터 세트가 훈련되고 테스트되며, 우리는 훈련된 SVM의 예측 능력을 기록합니다. 안정적인 성능을 얻기 위해, 우리는 각 화폐의 임의 분할을 1000 번 반복합니다.

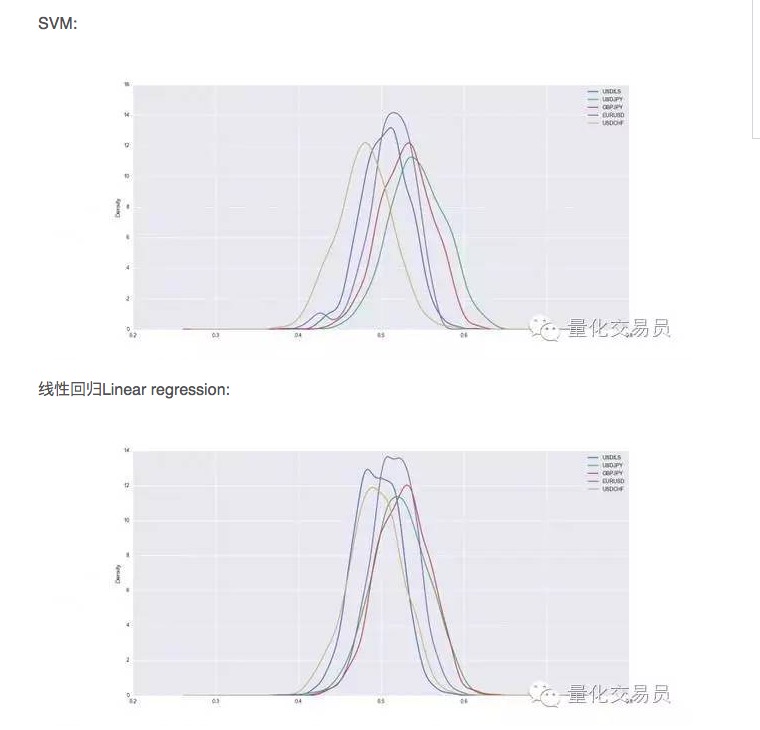
그래서 SVM가 단순한 선형 회귀보다 우수하지만 성능의 차이는 약간 높습니다. 예를 들어, 달러 대 일본 달러의 경우 평균적으로 예측 가능한 신호는 전체의 54%를 차지합니다. 이것은 꽤 좋은 결과이지만 좀 더 자세히 살펴 보겠습니다!

테드는 제프의 사촌인데, 물론 코리안이기도 하지만, 제프보다 훨씬 똑똑하다. 테드는 훈련된 샘플셋을 보고, 무작위 베팅을 하지 않는다. 그는 항상 훈련된 샘플셋의 가장 흔한 출력에서 신호를 내린다. 이제 똑똑한 테드를 기준으로 하자:

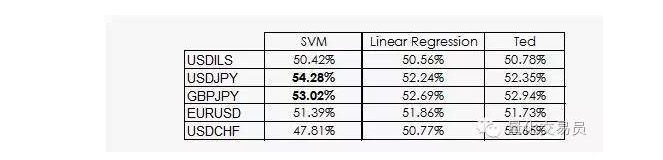
우리가 보듯이, 대부분의 SVM의 성능은 단지 하나의 사실에서 비롯된다: 기계 학습은 분류가 선행과 같을 가능성이 없다는 것이다. 사실, 선형 회귀는 특징 공간에서 어떤 정보도 얻을 수 없다, 그러나 절단 (intercept) 은 회귀에서 의미가 있으며, 절단 (intercept) 은 특정 분류를 더 잘 수행하는 것과 관련이 있다.

조금 더 좋은 소식은 SVM 벡터 기계가 데이터에서 몇 가지 비선형 정보를 얻을 수 있다는 것입니다. 이것은 우리가 예측의 정확도를 2%로 제시할 수 있게 해줍니다.

불행히도, SVM 벡터 기계가 그 자체의 주요 단점을 가지고 있는 것처럼, 우리는 그것이 어떤 정보일지 모릅니다.

저자: P. López, quantdare에서 출판 위키미디어 공용호