알파견의 재치: 몬테카로 알고리즘, 한 번 봐도 알 수 있다!

올해 3월 9일부터 15일까지 한국 서울에서 5차례에 걸친 인간과 기계의 대결이 열렸다. 이 경기의 결과는 인간에게 패배로 끝났다. 세계 바둑 챔피언 리시시가 구글의 인공지능 프로그램인 알파고에게 1대 4로 패배했다. 그럼 알파고 (AlphaGo) 는 무엇이고, 이기는 열쇠는 어디에 있을까요? 여기서는 알파고 (AlphaGo) 의 알고리즘을 알아보겠습니다.

• ### 알파고와 몬테카로 알고리즘

신화통신에 따르면, 알파고 (AlphaGo) 는 구글 (Google) 의 딥마인드 (DeepMind) 팀에서 개발한 인-기계 (Go) 게임 프로그램으로, 중국 게임 팬들은 알파 狗 (알파 狗) 라고 불렀다.

지난 글에서 우리는 Google이 개발하고 있는 기계 학습을 위한 신경망 알고리즘에 대해 언급했는데, AlphaGo도 이와 비슷한 제품입니다.

중국자동화협회 부회장 겸 사무총장인 왕피유 (王飞跃) 는 프로그래머들이 골프를 숙지할 필요는 없다고 말하며, 골프의 기본 규칙을 알아야만 한다고 말했다. 알파고의 배후에 있는 것은 뛰어난 컴퓨터 과학자들로 구성된 집단이며, 정확히 말하면, 기계 학습 분야의 전문가들이다. 과학자들은 신경망 알고리즘을 이용하여, 체스 전문가들의 경기 기록을 컴퓨터에 입력하고, 컴퓨터가 스스로 자신과 경기를 하게 하고, 이 과정에서 끊임없이 학습 훈련을 하게 한다.

그래서 알파고가 스스로 학습해서 천재가 될 수 있는 열쇠는 무엇일까요? 그것은 몬테카로 알고리즘입니다.

몬테카로 알고리즘이란 무엇인가요? 이 문서는 몬테카로 알고리즘에 대한 설명입니다. 만약 바구니에 1,000개의 사과가 있다면, 눈을 감고 가장 큰 것을 찾을 때마다, 선택의 수를 제한할 수 없습니다. 그래서, 눈을 감고 하나씩은 무작위로 뽑아, 또 다른 하나를 무작위로 뽑아, 첫 번째와 비교하고, 큰 것을 남겨두고, 또 다른 하나를 무작위로 뽑아, 이전과 비교하고, 큰 것을 남겨두고도 됩니다. 이런 식으로 반복해서, 더 많은 수를 뽑으면, 가장 큰 사과를 뽑는 확률이 더 커집니다. 하지만, 당신이 1,000개의 사과들을 모두 한번 선택하지 않는 한, 당신이 최종적으로 가장 큰 것을 뽑을 수 없다는 것은 확실하지 않습니다.

즉, 몬테카로 알고리즘은 샘플이 많을수록 최적의 솔루션을 찾을 수 있지만, 10,000개의 사과가 있다면 더 큰 것을 찾을 수 있다는 것을 보장하지는 않습니다.

라스베가스의 알고리즘과 비교할 수 있습니다. 통설에 따르면, 만약 잠금쇠가 있고, 1000개의 열쇠가 선택되는데, 오직 1개만이 옳다고 한다. 그러므로 매번 무작위로 1개의 열쇠를 가지고 시도하고, 열지 못하면 다시 1개를 교체한다. 시도하는 횟수가 많을수록, 가장 좋은 해를 열 수 있는 기회는 더 커지지만, 열기 전에, 그 잘못된 열쇠는 쓸모가 없다.

따라서 라스베가스 알고리즘은 가능한 최선의 해결책이지만 반드시 찾을 수 없다. 1,000개의 열쇠 중에서, 잠금쇠를 열 수 있는 열쇠가 하나도 없다고 가정하면, 진짜 열쇠는 1001번째 열쇠이지만, 표본에 1001번째 알고리즘이 없으므로 라스베가스 알고리즘은 잠금쇠를 열 수 있는 열쇠를 찾을 수 없다.

알파고의 몬테카로 알고리즘 특히 인공지능에 있어서는 매우 어려운 게임으로, 컴퓨터가 알아내기 힘든 많은 종류의 게임들이 있다. 왕 이 말했다: 첫째, 고아 게임의 가능성은 너무 많다。 고아 게임의 각 단계의 가능 하법은 매우 많으며, 체스 선수가 시작할 때 19×19=361가지 낙점 선택이 있다。 한 경기 150회 중 고아에서 발생할 수 있는 상황은 10170가지에 달한다。 둘째, 규칙은 너무 미세하며, 어느 정도 낙점 선택은 경험 축적으로 형성된 직관에 의존한다。 또한, 고아의 체스 경기에서, 컴퓨터는 체스의 장단점을 구분하기 어렵다。 따라서, 고아 도전은 인공지능의 ?? 아폴로 계획 ?? 이라고 부른다。

알파고는 몬테카로 알고리즘의 일부일 뿐만 아니라, 몬테카로 알고리즘의 업그레이드 버전이기도 합니다.

알파고는 몬테카로 트리 검색 알고리즘과 두 개의 심도 신경망의 협력을 통해 체스를 완성했다. 리시지와의 대결 전에, 구글은 먼저 알파고 개신아리의 신경망을 인간 쌍의 거의 3천만 가지의 걸음으로 훈련시켜 인간 프로 체스 선수들이 어떻게 떨어질지 예측하도록 배웠다. 그리고 더 나아가, 알파고가 스스로 체스를 하게 하여, 거대한 규모의 완전히 새로운 체스표를 만들어냈다. 구글 엔지니어는 알파고가 매일 백만 개의 걸음수를 시도할 수 있다고 선언했다.

그들의 임무는 협동적으로 유망한 체스 동작을 골라내어, 명백한 실점을 없애고, 컴퓨터가 할 수 있는 범위 내에서 계산량을 조절하는 것이다.

중국과학원 자동화 연구소 연구원 이진진 (易建强) 은, ?? 전통 체스 소프트웨어, 일반적으로 폭력적인 검색을 사용하며, 딥 블루 컴퓨터를 포함하여, 모든 가능한 결과에 대한 검색 트리를 구축한다 (각 결과는 나무의 한 가지 열매이다) 필요에 따라 가로질러 검색한다. 이 방법은 체스, 점프 등에서도 어느 정도 실현 가능하지만, 고구에 대해서는 실현할 수 없다, 왜냐하면 고구이 각 19개의 라인을 가로질러 있고, 낙점의 가능성은 컴퓨터가 나무를 구성할 수 없을 정도로 크기 때문이다 (과 열매가 너무 많다).

가치는 더 설명하기를, 심층 신경망의 가장 기본적인 단위는 우리 인간의 뇌의 뉴런과 비슷하며, 여러 계층이 연결되어 있는 것은 마치 인간의 뇌의 신경망과 같다. AlphaGo의 두 개의 신경망은 전략 네트워크와 평가 네트워크이다.

전략 네트워크는 주로 낙하 전략을 생성하기 위해 사용된다. 체크를 치는 과정에서, 자신이 어떻게 해야 하는지를 생각하지 않고, 인간의 우수한 손이 어떻게 될지 생각한다. 즉, 입력된 체크판의 현재 상태에 따라 인간의 다음 체크가 어디에 있을지를 예측하고, 인간의 사고에 가장 적합한 몇 가지 가능한 방법을 제시한다.

그러나 전략 네트워크는 자신이 내놓을 수 있는 단계가 얼마나 좋은지 알 수 없고, 단지 그것이 인간과 같은 단계가 될 수 있는지 알고 있을 뿐인데, 이때는 평가 네트워크가 작용할 필요가 있다.

가치는 이렇게 말한다: ?? 평가 네트워크는 가능한 모든 방법들에 대해 전체 디스플레이의 상황을 평가하고, 그 다음에는 승률 을 준다. 이 값들은 몬테카로 트리 검색 알고리즘에 피드백되어, 위와 같은 과정을 반복하여 승률 이 가장 높은 걸음을 선보인다. 몬테카로 트리 검색 알고리즘은 전략 네트워크가 승률 이 더 높은 곳에서만 계속 진행되도록 결정하고, 따라서 특정 경로를 버리고, 하나의 경로를 계산하지 않고 블랙으로 간다.

알파고는 이 두 가지 도구를 사용하여 상황을 분석하고, 각 하위 전략의 장단점을 판단합니다. 마치 인간 체스 선수가 현재의 상황을 판단하고 미래의 상황을 추론하는 것과 같습니다. 몬테카로 트리 검색 알고리즘을 사용하여 예를 들어 20 단계의 미래 상황을 분석하면, 하위 전략이 이길 확률이 높은 곳을 판단할 수 있습니다.

하지만 알파고의 핵심은 몬테카로 알고리즘입니다.

두 개의 작은 실험 마지막으로, 몬테카로 알고리즘의 두 가지 작은 실험을 살펴봅시다.

• ### 1. 둘레율 pi 를 계산한다.

원리: 먼저 사각형을 그리고, 그 안에 절단된 원을 그린다. 그리고는 이 사각형 안에 있는 무작위 도면점을 설정한다. 원 안에 있는 도면은 P로, P=경의 면적/사각형의 면적이다. P=(Pi*R*R)/(2R*2R) = Pi/4 즉 Pi=4P

다음 단계: 1. 원심점을 원점으로 설정하고, R을 반지름으로 원을 만들면, 첫 번째 사각형의 ¹⁄₄ 원의 면적은 Pi이다*R*R/4 2. 이 ¹⁄₄ 원의 외면 사각형의 좌표는 ((0,0) ((0,R) ((R,0) ((R,R)) 이고, 이 사각형의 면적은 R*R 3. 즉석에서 점들을 (X,Y) 를 취해서 0<=X<=R 그리고 0<=Y<=R, 즉 점들은 사각형 안에 있다 4. 공식 X*X+Y*Y. 5. 모든 점 ((즉 실험 횟수) 의 숫자가 N이고, ¹⁄₄ 원 안의 점 (((단계 4의 점) 의 숫자가 M인 경우

P=M/N 이니까 Pi=4*N/M 사진 1

M_C(10000) 실행 결과 3.1424

• ### 2. 몬테카로 모의 탐색 함수의 극한값, 지역 극한값에 빠지는 것을 피할 수

# 간격으로[-2,2]에 임의로 숫자를 생성하고, y를 찾아내서,[-2,2]의 극한값 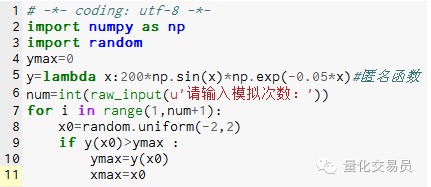사진 2

1000번의 시뮬레이션 결과 최대값은 185.12292832389875 (정확함)

여기 보시면 알 수 있을 겁니다. 코드는 손으로 쓸 수 있습니다. 재미있네요. 위키미디어 공용호