시각적 직관적 감각 7개의 일반적인 서열 알고리즘

전략 작성할 때, 프로그램 코드는 필연적으로 데이터 정렬을 필요로 하는 상황에 부딪히기 때문에, 최소한의 시스템 비용 (시간, 시스템 자원) 을 사용하여 과학적인 프로그램을 어떻게 설계할 수 있습니까?

• ### 1. 빠른 순서

소개: 빠른 순서는 토니 홀 (Tony Hall) 이 개발한 순서 알고리즘이다. 평균적인 상황에서 n개의 항목을 순서화하는 데는 O (n) 로그 n (n) 조치가 필요하다. 최악의 경우에는 O (n) 로그 n (n) 조치가 필요하다. 그러나 이러한 상황은 흔하지 않다. 사실, 빠른 순서는 종종 다른 O (n) 로그 n (n) 알고리즘보다 훨씬 빠르다. 왜냐하면 그것의 내부 순환 (inner loop) 은 대부분의 구조에서 매우 효율적으로 구현될 수 있고, 대부분의 현실 세계의 데이터에서 설계 선택을 결정할 수 있기 때문에 필요한 시간을 줄일 수 있기 때문이다. 다음 단계: 그리고, 우리는 이 행렬에서 하나의 요소를 선택합니다. 재배열열열은, 기준값보다 작은 모든 요소를 기준값의 앞에 배치하고, 기준값보다 큰 모든 요소를 기준값의 뒤에 배치한다. 이 분할이 퇴출된 후, 이 기준값은 배열의 중간 위치에 있다. 이것은 분할 (partition) 동작이라고 한다. 회귀적으로 ((recursive) 기준값 요소보다 작은 하위수열과 기준값 요소보다 큰 하위수열을 정렬한다. 정렬 효과:

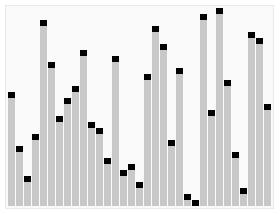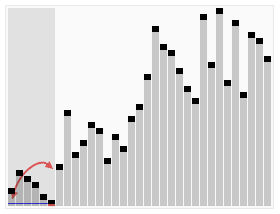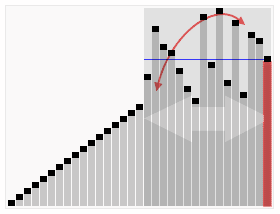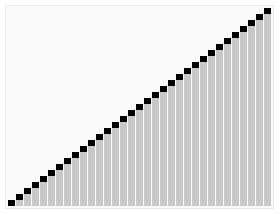
• ### 2. 합성 순서

소개: 병합 정렬 (Merge sort) 은 병합 연산에 기반한 효과적인 정렬 알고리즘이다. 이 알고리즘은 분배법 (Divide and Conquer) 을 사용하는 매우 전형적인 응용이다. 다음 단계: 요청 공간, 두 개의 이미 정렬된 시퀀스의 합산된 시퀀스를 저장하기 위한 공간 두 개의 포인터를 설정하여, 각 초기 위치는 두 개의 정렬 된 시퀀스의 시작 위치입니다 두 지점의 요소를 비교하고, 비교적 작은 요소를 선택하여 통합 공간에 넣고, 지점을 다음 위치로 이동합니다. 3단계를 반복해서 다른 서열의 나머지 모든 요소를 통합 서열의 끝에 직접 복사합니다. 정렬 효과:

• ### 3. 무더기 배열

소개: Heapsort () 은 heapsort이라는 데이터 구조를 이용하여 설계된 정렬 알고리즘이다. heapsort은 거의 완전한 이중 나무의 구조이며, 또한 heapsort의 특성을 만족시킨다. 즉, 하위 노드의 키값 또는 인덱스는 항상 그 부모 노드보다 작거나 크다. 다음 단계: (그것보다 더 복잡해, 인터넷으로 직접 찾아보세요.) 정렬 효과:

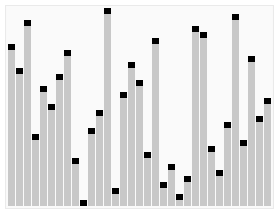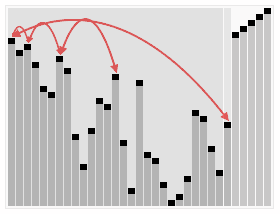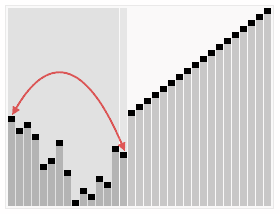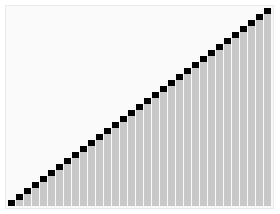
• ### 4. 순서를 선택하세요

소개: 선택 정렬 (Selection sort) 은 간단한 직관적인 정렬 알고리즘이다. 이 알고리즘은 다음과 같이 작동한다. 먼저 정렬되지 않은 서열에서 최소의 요소를 찾아서, 정렬 서열의 시작 위치로 저장하고, 그 다음, 나머지 정렬되지 않은 요소에서 최소의 요소를 계속 찾고, 그 다음으로 정렬 서열의 끝으로 넣는다. 정렬 효과:

• ### 5. 부풀어오르는 순서

소개: 버블 서트 (Bubble Sort, 타이완어:泡泡排序, 버블 서트) 는 간단한 서팅 알고리즘이다. 그것은 반복적으로 서핑하려는 수를 방문하고, 한 번에 두 개의 요소를 비교하고, 만약 그들의 순서가 잘못되면 그들을 교환한다. 서열을 방문하는 작업은 교환이 더 이상 필요하지 않을 때까지 반복적으로 수행된다. 즉, 서열은 서열이 완료되었다. 이 알고리즘의 이름은 점점 더 작은 요소가 교류를 통해 서서히 서열의 꼭대기에 떠돌기 때문이다. 다음 단계: 인접한 요소들을 비교한다. 첫 번째 요소가 두 번째 요소보다 크면, 둘을 교환한다. 모든 인접한 요소들에 대해 동일한 작업을 수행하고, 첫 번째 요소부터 마지막 요소까지 진행한다. 이 시점에서, 마지막 요소는 가장 큰 숫자여야 한다. 모든 요소에 대해 위의 단계를 반복합니다. 마지막 하나만 빼고요. 계속적으로 점점 더 적은 수의 요소에 대해 위의 단계를 반복하여, 어떤 숫자 쌍도 비교가 필요하지 않을 때까지 반복한다. 정렬 효과:

• ### 6. 삽입 순서

소개: 삽입 정렬 (Insertion Sort) 의 알고리즘 설명은 간단한 직관적인 정렬 알고리즘이다. 그것의 작동 원리는 순서로 된 순서를 구축하여, 정렬되지 않은 데이터에 대해, 정렬 된 순서에서 뒤로 앞으로 스캔하여, 해당 위치를 찾아서 삽입한다. 삽입 정렬은 구현에서, 일반적으로 in-place 정렬 (즉, O (1) 의 추가 공간을 사용하는 정렬) 을 사용합니다. 따라서 뒤로 앞으로 스캔하는 과정에서, 정렬 된 요소를 단계적으로 뒤로 이동하여 최신 요소에 삽입 공간을 제공해야합니다. 다음 단계: 첫 번째 요소부터 시작해서, 그 요소는 이미 정렬되었다고 볼 수 있습니다. 다음 요소를 뽑아서, 이미 정렬된 요소의 서열에서 뒤로 앞으로 스캔합니다. 만약 이 요소가 새로운 요소보다 크다면, 다음 위치로 이동한다. 단계 3를 반복하여 새로운 요소보다 작거나 같을 때까지 정렬 된 요소를 찾습니다. 이 위치에 새로운 요소를 삽입합니다. 2단계를 반복합니다. 정렬 효과: (현재)

• ### 7. 힐 서열

소개: 힐 정렬 (영어: Hill sorting, 영어: decreased-incremental sorting) 은 삽입 정렬의 빠르고 안정적인 개선 버전이다. 힐 서열은 삽입 서열의 다음 두 가지 성질에 따라 개선 방법을 제안합니다: 1., 삽입 정렬은 거의 정렬 된 데이터에 대해 작업 할 때 효율성이 높습니다. 즉, 선형 정렬의 효율성을 달성 할 수 있습니다. 2 하지만 삽입 정렬은 일반적으로 비효율적입니다. 왜냐하면 삽입 정렬은 한 번에 하나의 데이터만 이동할 수 있기 때문입니다.

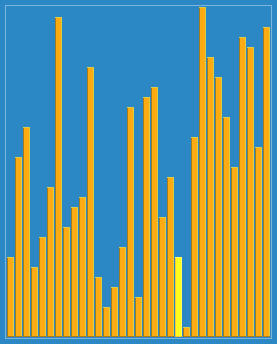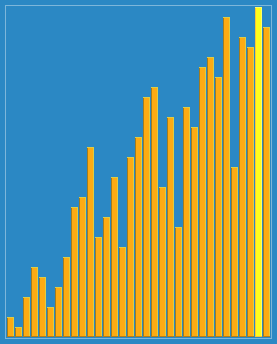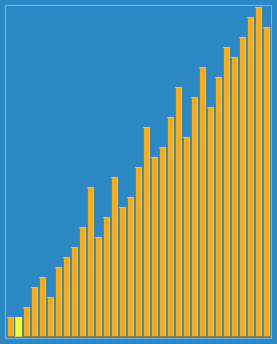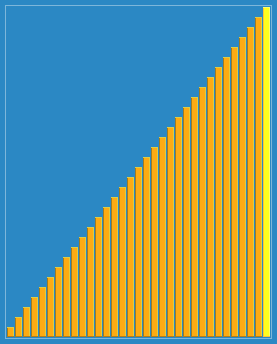
제가 가장 많이 사용하는 것은 붓기법 (가장 간단한 방법) 입니다.