은닉 마르코프 모델

• ### 1. 아는 것

오늘 우리는 HMM의 간단한 주식 적용에 대해 알아보고자 합니다.

마르코프 체인 (Markov Chain) 은 매우 고급스럽게 들릴 수 있지만, 어떤 것이 있는지 전혀 알 수 없습니다.

마르코프 사슬은 안드레 마르코프 (A.A. Markov, 1856-1922) 의 이름을 따서 붙여진 이름이다. 수학에서 마르코프 성질의 산발적 사건의 무작위적 과정을 가리킨다. 주어진 현재 지식이나 정보의 상황에서 과거 (즉, 현재 이전의 역사적 상태) 는 미래를 예측하는 데 무관하다 (즉, 현재 이후의 미래 상태).

이 과정에서, 각 상태의 이동은 이전 n개의 상태에만 의존한다. 이 과정은 1개의 n 계층의 모델이라고 불리는데, 여기서 n는 이동 상태의 영향을 미치는 수이다. 가장 간단한 마르코프 과정은 1단 과정이며, 각 상태의 이동은 이전 하나의 상태에만 의존한다.

• ### 예제 2

수학적인 표현은 다음과 같습니다.

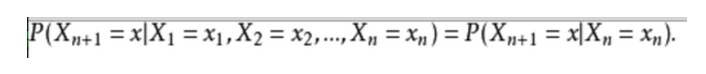
일상의 예를 들어서, 우리는 현재 날씨의 상황에 따라 미래의 날씨 상황을 예측하기를 원합니다. 하나의 방법은 이 모델의 각 상태가 전의 상태에만 의존한다고 가정하는 것입니다. 즉, 마르코프 가설, 이 가설은 이 문제를 극도로 단순화 할 수 있습니다. 물론, 이 예제도 다소 비현실적입니다. 그러나, 이러한 단순화 된 시스템은 우리의 분석에 도움이 될 수 있으므로, 우리는 일반적으로 이러한 가설을 받아들이고, 왜냐하면 그러한 시스템이 우리에게 유용한 정보를 제공 할 수 있다는 것을 알고 있기 때문입니다.

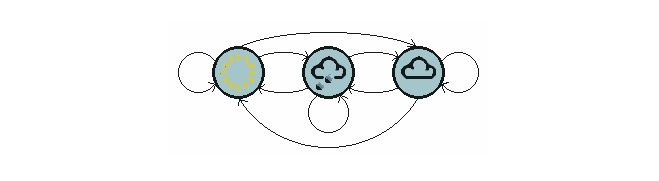
위 그림은 날씨가 변하는 모델을 보여줍니다.

N개의 상태를 포함하는 1단 과정에는 N2개의 상태 전환이 있다. 각각의 전환의 확률은 상태 전환 확률이라 불리며, 즉 한 상태에서 다른 상태로의 전환의 확률이다. 이 N2개의 확률은 모두 상태 전환 매트릭스로 나타낼 수 있다. 위의 날씨 예의 상태 전환 매트릭스는 다음과 같다:

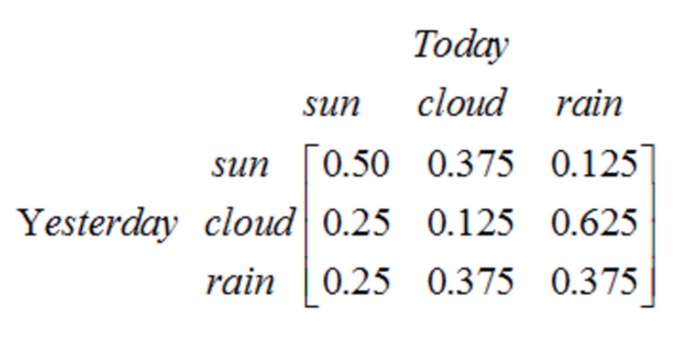
이 행렬은 만약 어제의 날씨가 흐린다면 오늘의 날씨가 맑을 확률이 25%이고, 12.5%의 확률이 맑을 것이고, 62.5%의 확률이 비가 올 것이라는 것을 나타냅니다. 분명히 행렬의 각 행의 합은 1 ≠ 1 입니다.

이런 시스템을 초기화하려면 초기 확률 벡터가 필요합니다.

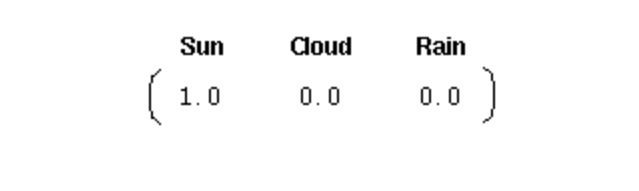
이 벡터는 첫날이 맑은 날이라는 것을 나타냅니다. 여기서 우리는 위의 1단 마르코프 과정에 대해 다음의 세 부분을 정의합니다:

날씨: 맑고, 은 날씨, 비가 오네요.

초기 벡터: 시간이 0일 때 시스템의 상태를 정의하는 확률.

상태 전환 매트릭스: 모든 기상 변환의 확률. 이렇게 묘사될 수 있는 모든 시스템은 마르코프 과정이다.

그러나 마르코프 과정이 충분히 강력하지 않을 때는 어떻게 해야 할까요? 어떤 경우에는 마르코프 과정이 우리가 발견하고자 하는 패턴을 설명하기에 충분하지 않습니다.

예를 들어 우리의 주식시장, 만약 단지 시장을 관찰한다면, 우리는 그날의 가격, 거래량 등의 정보를 알 수 있을 뿐이지만 현재 주식시장이 어떤 상태에 있는지 알 수 없다 ((부어시장, 곰시장, 흔들림, 반발 등), 이 경우 우리는 두 가지 상태 집합을 가지고 있다. 관찰 가능한 상태 집합 ((주식시장 가격 거래량 상태 등) 과 숨겨진 상태 집합 ((주식시장 상태)) 을 가지고 있다. 우리는 주식시장의 가격 거래량 상태와 마르코프 가설에 따라 주식시장의 상태를 예측할 수 있는 알고리즘을 찾기를 바란다.

위와 같은 경우, 관찰 가능한 상태의 연속과 숨겨진 상태의 연속은 확률 관련되어 있다. 따라서 우리는 이러한 유형의 과정을 숨겨진 마르코프 과정과 숨겨진 마르코프 과정의 확률과 관련된 관찰 가능한 상태의 집합, 즉 숨겨진 마르코프 모델로 모델링 할 수 있다.

숨겨진 마르코프 모델 (영어: Hidden Markov Model) 은 미지의 임의 변수를 포함하는 마르코프 과정을 묘사하는 통계적 모델이다. 그 난이도는 관찰 가능한 변수 중에서 그 과정의 임의 변수를 결정하고, 그 다음에는 이러한 변수들을 이용하여 추가적인 분석을 하는 것이다. 아래 그림은 x가 임의 상태를, y가 관찰 가능한 출력을, a가 상태 전환 확률을, b가 출력 확률을 나타내는 3개의 상태의 숨겨진 마르코프 모델 상태 이동 도표이다.

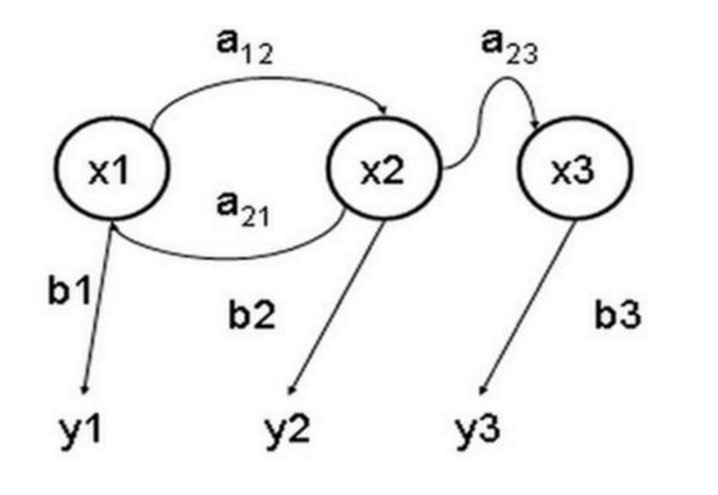
모자의 예를 들어 설명하자면: 제 손에 세 개의 다른 모자가 있다고 가정해 봅시다. 첫 번째 모자는 우리가 흔히 사용하는 모자입니다. (이 모자를 D6라고 부릅니다.) 6개의 면으로, 각 면은 (1,2,3,4,5,6) 1/6의 확률로 나타납니다.

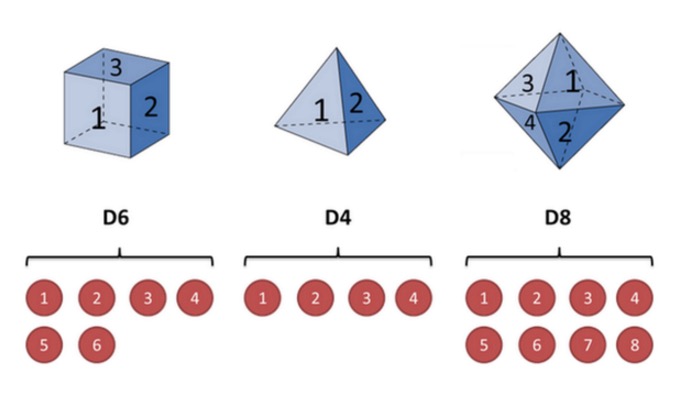
3개의 에서 1을 선택해서 1/3의 확률로 을 다고 가정해 봅시다. 그리고 우리는 1,2,3,4,5,6,7,8의 1을 습니다. 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복해서 반복

이 수열은 가시 상태 사슬이라고 합니다. 하지만 가시 말코프 모델에서는 가시 상태 사슬 뿐만 아니라, 가시 상태 사슬도 있습니다. 이 예제에서, 가시 상태 사슬은 당신이 사용하는 의 순서입니다. 예를 들어, 가시 상태 사슬은 다음과 같을 수 있습니다: D4 D6 D8 D6 D4 D8 D6 D6 D4

일반적으로 HMM에서 말하는 마르코프 사슬은 실재 상태 사슬을 의미하는데, 실재 상태 (子) 사이에 변환 확률이 있기 때문이다. 이 예제에서 D6의 다음 상태는 D4, D6, D8의 확률은 1/3이다. D4, D8의 다음 상태는 D4, D6, D8의 변환 확률도 1/3이다.

마찬가지로, 가시적인 상태 사이에 변환 확률이 없어도, 암시적인 상태와 가시적인 상태 사이에 출력 확률이라고 하는 확률이 있다. 우리의 예에서, 6면 ((D6) 가 1을 출력할 확률은 1/6이다. 2,3,4,5,6을 출력할 확률도 1/6이다. 우리는 또한 출력 확률에 대해 다른 정의를 내릴 수 있다. 예를 들어, 나는 바둑이 손발로 움직이는 6면 을 가지고 있는데, 1을 뽑는 확률이 더 크며, ¹⁄₂, 2,3,4,5,6을 뽑는 확률은 1/10이다.

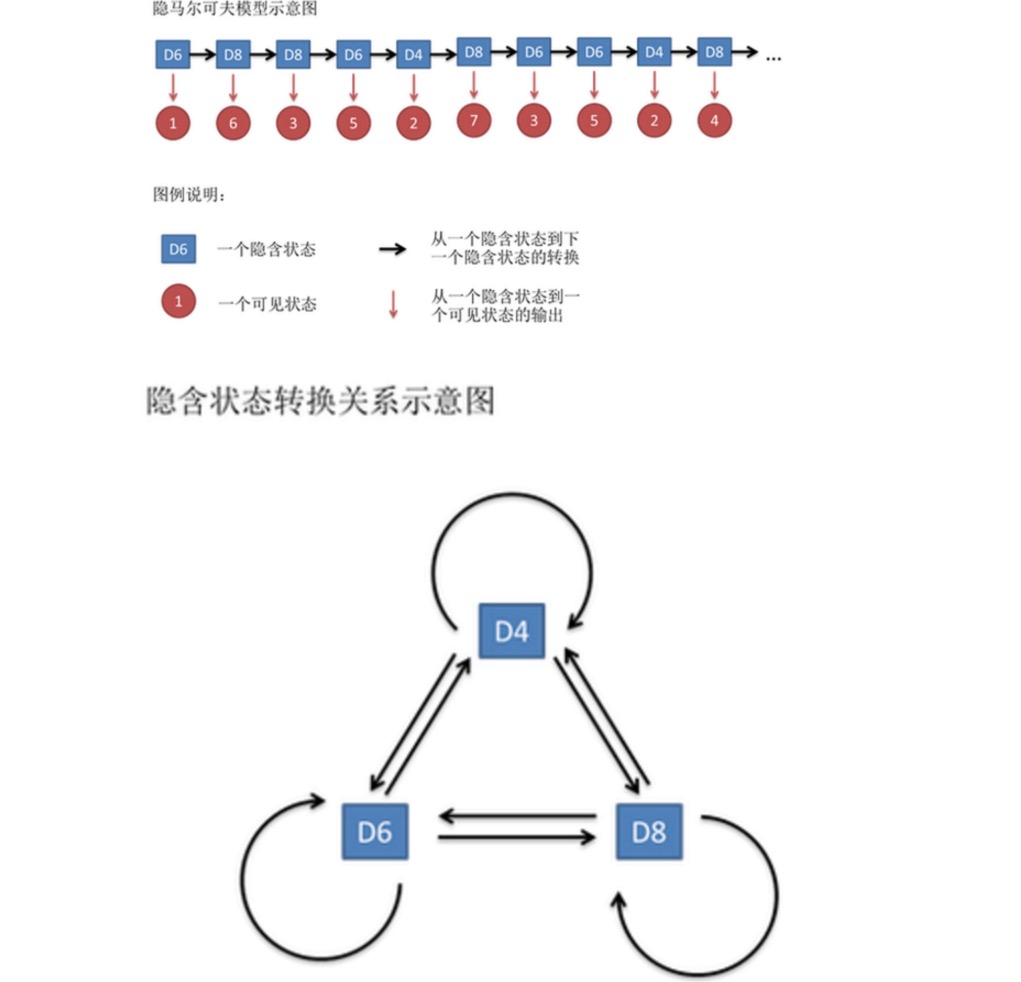
사실 HMM의 경우, 모든 숨겨진 상태 사이의 변환 확률과 모든 숨겨진 상태에서 모든 가시적인 상태로의 출력 확률을 사전에 알고 있다면, 시뮬레이션을 하는 것이 상당히 쉽다. 그러나 HMM 모델을 적용할 때, 종종 일부 정보가 누락된다. 때때로 당신은 이 몇 개 있고, 각 이 무엇인지 알고 있지만, 이 나오는 의 순서를 알지 못한다. 때로는 당신은 단지 의 결과를 여러 번 보았고, 나머지는 아무것도 모른다. 응용 알고리즘이 이러한 누락된 정보를 추정한다면, 매우 중요한 문제가 된다.

HMM 모델과 관련된 알고리즘은 크게 세 가지로 분류되며, 각각 세 가지 문제를 해결한다:

• 이 몇 개나 있는지 알고 싶고, 각 이 무엇인지 알고 싶고, 이 뽑은 결과에 따라 어떤 이 나오는지 알고 싶다.

• 이 몇 개 있는지 알고 싶네요. (숨겨진 상태의 수), 각 이 무엇인지 알고 싶네요. (변환 확률), 이 내린 결과에 따라 (보인 상태 사슬), 이 결과를 내리는 확률을 알고 싶습니다.

• 이 몇 개나 있는지 알고, 각각의 이 무엇인지 모르고, 많은 의 결과를 관찰하고, 각각의 이 무엇인지 반추적으로 추론하고 싶습니다.

  만약 상주에서의 문제를 해결하려면, 우리는 문제 1과 문제 3를 해결해야 합니다. 다음 기사에서는 어떻게 이 문제를 해결할 수 있는지 살펴볼 것입니다.

모니코드 (Moneycode)