공적분의 직관적 이해

참고: 이 글은 통합의 개념을 직관적으로 소개하고, 그 기본적 의미와 동기가 무엇인지, 그리고 간단한 응용 시나리오를 이해하도록 돕습니다.

• 통합 소개

여기서는 단지 통합의 직관적인 정의를 알려주고자 합니다. 엄격한 수학적 기호의 정의와 엄격한 공식 추론을 포함하지 않습니다.

만약 관심이 있다면, 위키백과 Cointegration에 참고하세요. 양자 수업은 앞으로 그 깊이 있는 내용을 탐구할 것입니다.

왜 평평해야 하는가?

하지만, 이 모든 것이 ‘동일성’에 불과하다.

간단히 말해서, 평형성 (stationarity) 은 시퀀스가 시간이 지남에 따라 안정적으로 변하지 않는 성질이며, 이는 데이터의 분석 예측을 할 때 우리가 매우 좋아하는 성질이다. 시간 시퀀스 데이터가 평형하다면, 그 평균과 차이는 변하지 않는 것을 의미하며, 따라서 우리는 시퀀스에 몇 가지 통계 기술을 편리하게 사용할 수 있다. 평형과 비평형의 시퀀스가 직관적으로 어떻게 생겼는지에 대한 예를 먼저 보자.

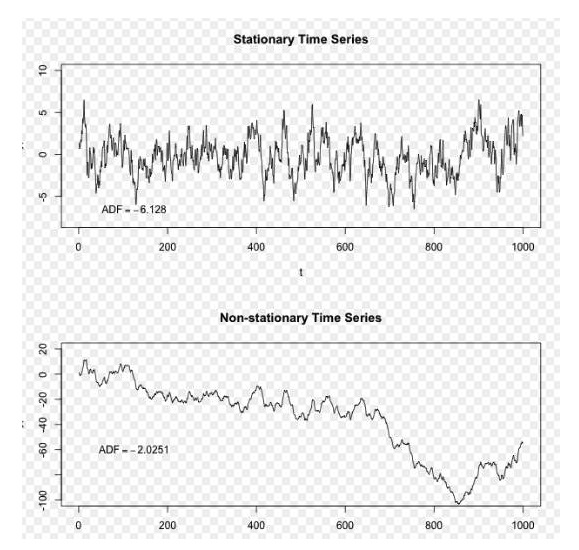
위키피디아

위의 그림에서, 위쪽의 시퀀스는 평평한 시퀀스이며, 우리는 그것이 항상 장기간 평균값을 중심으로 변동하는 것을 볼 수 있습니다. 아래쪽의 시퀀스는 비평평평한 시퀀스이며, 우리는 그것의 장기간 평균값이 변동하는 것을 볼 수 있습니다.

응용 예로, 어떤 자산의 가격 순서 (또는 두 순서 사이의 가격 차) 가 평평하다면, 그 값이 평균값에서 벗어나면, 그 값이 미래에 어느 시점에서 그 평균값으로 돌아갈 것을 기대할 수 있다. 우리는 이 특성을 이용하여 투자하여 수익을 얻을 수 있다. 한 주식의 장기간 평균값이 9달러이고, 현재 가치가 8달러라고 가정한다. 검사를 거친다면, 이 주식의 역사적 순서가 평평한 특성을 지니고 있다고 생각하며, 이 평평성이 유지될 수 있다고 가정하면, 이 주식을 사서, 그 가격이 미래에 9달러로 돌아가는 것을 기다리며, 1달러의 이익을 얻을 수 있다.

이것은 주식 가격의 순서입니다.

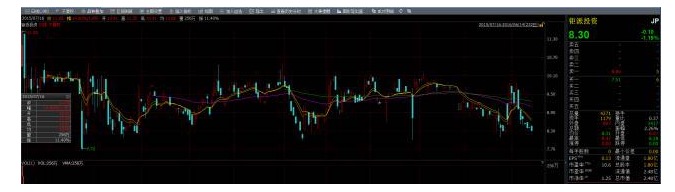
평형성은 매우 유용하지만, 현실에서, 대부분의 주식은 평형하지 않습니다, 그렇다면 우리는 평형성 특성을 활용하여 이익을 얻을 수 있습니까? 대답은 예, 이 때 연동관계 ((cointegration) 가 등장합니다! 두 개의 일련의 세트들이 평형하지 않지만, 그들의 선형적 조합이 평형한 일련의 결과를 얻을 수 있다면, 우리는 이 두 개의 시간 계열 데이터 세트들이 연동적 특성을 가지고 있다고 말할 수 있습니다. 우리는 또한 이 조합의 계열에 통계적 특성을 사용할 수 있습니다. 그러나, 연동관계는 상관관계 (correlation) 가 아니라는 점을 지적할 필요가 있습니다.

예를 들어, 두 세트의 시간 순서 데이터의 차이는 평평한 경우, 우리는 이 차이의 평평성에 따라 투자 수익을 올릴 수 있습니다: 두 주식의 가격이 너무 큰 때, 평평성에 따라 우리는 가격 차이는 수렴할 것으로 예상하고, 따라서 낮은 가격을 가진 주식을 구입하고, 높은 가격을 가진 주식을 판매하고, 가격이 돌아 오는 것을 기다리는 동안 역으로 작동하여 수익을 올릴 수 있습니다.

이것이 바로 쌍거래의 기원이 되는 것입니다.

• 안정성 및 검사 방법

엄밀히 말해서, 평형성은 엄격히 평형 (strictly stationary) 과 약한 평형 (weak stationary) 으로 나눌 수 있다. 엄격히 평형 (strictly stationary) 은 일련의 항상 변하지 않는 분포 함수를 나타내는 것이고, 약한 평형 (weak stationary) 은 일련의 변하지 않는 상수의 서술적 통계량을 나타내는 것이다. 모든 강한 평형 순서는 약한 평형성 특성을 만족하지만, 반대로는 성립하지 않는다. 우리가 일반적으로 말하는 평형성은 약한 평형이다. 시간 순서 분석에서 우리는 일반적으로 단위 뿌리 검사를 통해 하나의 과정이 약한 평형 (weak stable) 인지를 판단한다.

예를 들어서

먼저, 상관관계는 상관관계가 아니라는 점을 지적해야 합니다. 우리는 인공적으로 두 개의 데이터 세트를 구성하여 직관적으로 상관관계를 봅니다. import numpy as np import pandas as pd import seaborn import statsmodels import matplotlib.pyplot as plt from statsmodels.tsa.stattools import coint

구조 데이터

먼저, 우리는 두 개의 데이터 세트를 구성하고, 각 데이터 세트의 길이는 100이다. 첫 번째 데이터 세트는 100을 더한 하향 추세 항목을 더한 표준 정형 분포를 더한다. 두 번째 데이터 세트는 첫 번째 데이터 세트의 기초에 30을 더하고, 추가 표준 정형 분포를 더한다.

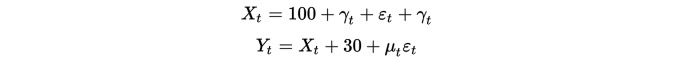
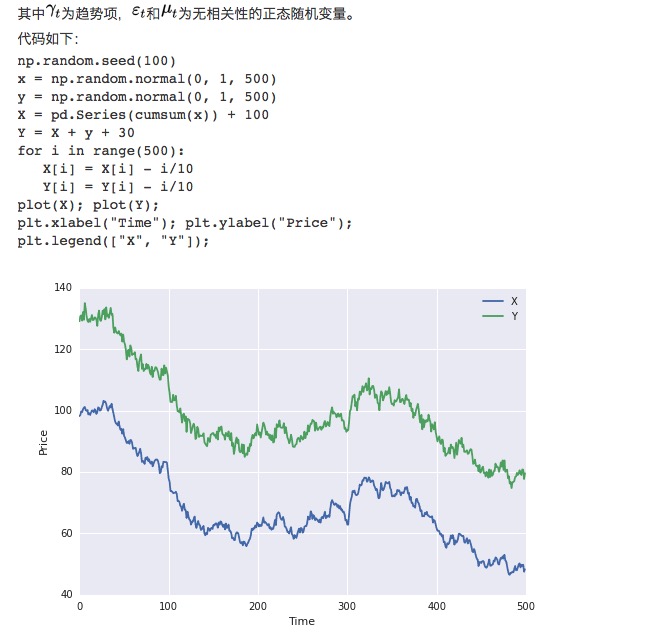
명백히, 이 두 세트의 데이터는 모두 평평하지 않다, 왜냐하면 평균값이 시간의 변화와 함께 변하기 때문이다. 그러나 이 두 세트의 데이터는 서로 대칭 관계에 있다, 왜냐하면 그들의 차차열이 평평하기 때문이다:

plot(Y-X); plt.axhline((Y-X).mean(),color=“red”, linestyle=“–”); plt.xlabel(“Time”); plt.ylabel(“Price”); plt.legend([“Y-X”, “Mean”]);

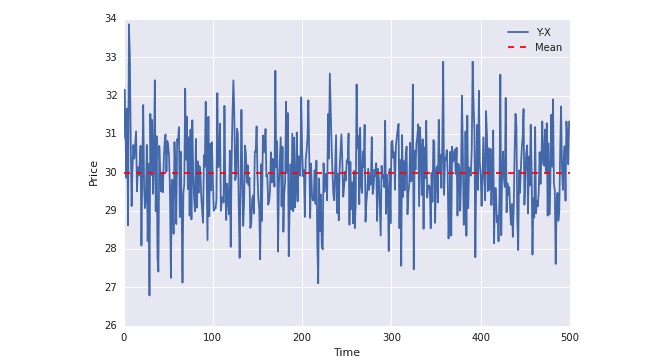
위의 그림에서 볼 수 있듯이, 파란 선은 항상 평균값을 중심으로 변동한다. 평균값은 시간에 따라 변하지 않는다.

• 결론

만약 수학적인 관점에서만 통합을 설명한다면, 훨씬 더 복잡해 질 것이고, 앞으로의 정량화 수업에 포함될 것이다. 우리는 단지 [level-0) ]의 수준에 대한 간단한 소개를 하고자 하는데, 목표는 사람들이 더 잘 통합과 실제적인 응용을 결합하도록 하는 것이다.

양적 수업을 진행하고, 공유하고,