?? 리스크 소 스 (四) ?? 모버와 신의 곡선

지난번호에 따르면, 야코브 베르누리는 사망할 때 확률론에 관한 자신의 책집 추측법을 출판하지 않았다. 그의 필사본을 정리하는 임무를 그의 조카 니콜라스 2세 베르누리 (니콜라스 2세 베르누리) 에게 맡겼다. 니콜라스 (니콜라스 2세 베르누리) 는 삼촌의 유언을 마친 후, 실제 확률에 대한 오차 수준을 연구하기 시작했다. 아마도 천재 명상 중에도 자신이 부지런하다고 느꼈기 때문에, 모프를 연구에 참여하도록 초대했다. 모브르 (Abraham de Moivre) 는 많은 곳에서 메브르 (梅弗) 로 번역되어 있지만, 그의 초상화를 보고 난 후, 나는 후자의 이 번역법을 별로 지지하지 않는다. 원래 이 초청은 후세에 대한 찬송의 수 (ji) 학 (you) 界의 좋은 말을 성취할 수 있었다. 그러나 모브르 (莫弗) 는 거절했다. 그리고 그는 자신이 아직 충분히 강하지 않다고 생각했기 때문에 거절했다.

• 모버 모프는 사실 제이콥 베르누리보다 10살 정도 어린 나이로, 그의 생애 전체를 사실 소설로 묘사할 수 있다. 그 당시 프랑스는 가톨릭 분위기가 열광한 나라였고, 모프는 우연히도 우연히도 개신교 신자였다. 이후 프랑스 국왕 루이 14세는 프랑스의 개신교 신자들을 열등한 시민이라고 선언하는 법령을 내렸으며, 어린이는 개신교로 개종해야 했다. 이 조치는 프랑스에서 개신교를 근본적으로 종파로 규정했고, 모프는 그 때문에 2년 동안 감옥에 갇혔다. 감옥에서 나온 모프는 영국으로 도망쳤지만, 그는 결국 학계에서 교직을 얻지 못했지만, 그는 뉴턴과 친구였음에도 불구하고, 30세의 나이에 영국 왕실의 회원이 되었다. 모프는 평소에 다른 수학 교사들과 수들에게 생계를 유지하기 위해 자문을 제공했고, 일상생활을 유지하기 위해 수학을 기본으로 구성하는 것은 놀이와 욕설의 결과라고 말하며, 87세까지 프랑스에서 맹목적이었다.

그러나 우리는 여기서 ‘모버는 영원히 죽지 않는다’고 외칠 것이다! 1711년모버는 운의 측정에 관한 한 권의 을 출판했다. 그 당시 모버가 모버의 책장을 썼다면, 그 책장에 뉴턴의 추천 문구가 적혀 있었을 것이다. “모버 씨에게 물어봐라, 그는 이 부분에 대해 나보다 더 잘 알고 있다”.

하지만 당시에는 그렇지 않았기 때문에, 모버는 많은 저작권료를 받을 수 없었습니다.

당신은 우리가 지난 기사에서 했던 문제를 기억해야 합니다. (위험소설 (三): 伯努利少尉), 안에 있는 5000개의 석회석에 대해, 우리는 총 석회석의 비율을 추정하기 위해 25,500번의 잡기를 할 수 있습니다. 그러나 당신은 또한 25,500번의 반복적인 잡기가 너무 많다는 것을 발견해야 합니다.

미적분학과 파스카 삼각형의 방법을 이용한 모버는 그룹 샘플링 방법을 취했다. 그는 100개의 돌을 매번 에서 꺼내어, 검은색과 흰색의 돌의 비율을 기록한 후 다시 넣고, 같은 방식으로 추출했다. 이런 방법을 통해 모버는 당신이 기록한 비율과 실제 비율의 근사한 편차를 미리 알려줄 수 있고, 이 비율은 그들의 평균값 주위에 어떻게 분산되어 있는지 알려줄 수 있다.

이 말은 마치 익숙한 것처럼 느껴지거나 입에 들어와 그 이름을 부르고 싶었던 것 같습니까? 네, 이것이 우리가 알고있는 정형 분포입니다. 정형 분포의 곡선은 시계 모양의 곡선과 같으며, 대부분의 관측 값이 중앙에 모여 모든 관측 값의 평균에 가깝고, 평균에서 대칭적으로 양쪽 끝에 기울어지며, 평균의 양쪽 끝의 관측 값의 수는 동일합니다. 처음에는 곡선은 빠른 속도로 기울어지며, 양쪽 끝에서는 이러한 기울기가 평평해집니다. 이것은 평균에서 멀리 떨어진 관측 값이 나타나는 확률이 작다는 것을 의미합니다.

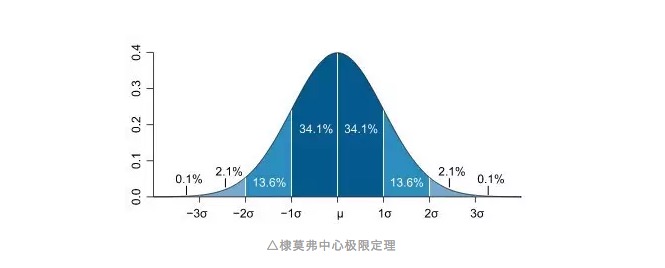
이렇게 해서 우리는 표준 격차의 개념을 도입할 수 있게 되었는데, 실제로는 공중호의 다른 기사에서 (왜 표준 격차인가? 대신의 눈에서 위험 측정) 우리는 이미 그것에 대해 언급한 적이 있다. 표준 격차는 실제로 관찰값이 평균과 오차하는 정도를 묘사한다. 또는 우리는 그것을 평균과 오차하는 단위로 이해한다. 정형 분포에 대해, 우리가 추출한 100개의 그룹 1의 오석의 비율 값은 대략 68%가 평균의 양쪽에 하나의 표준 격차의 범위 안에 떨어지며, 두 표준 격차의 범위는 대략 95%의 관찰 값을 포함할 수 있다.

신실한 신자로서, 모프는 시계 곡선이 신의 산물이라고 생각했다. 그의 견해에 따르면, 이러한 측정으로 우리는 불확실성을 극복하고, 나아가 모든 위험을 정복할 수 있다. 왜냐하면 곡선에는 모든 가능한 현상과 그 확률이 이미 묘사되어 있기 때문이다. 아마도 우연으로 인해 소위 편차가 발생하지만, 시간이 지남에 따라 이러한 편차는 우리가 요약하는 법칙에 영향을 미치지 않는다.

모프의 말을 우리 모두가 좋아하는 방식으로 설명하면, 실망은 가끔 전화번호를 수 없는 전화번호이며, 여러 번 시도해보고, 항상 답한다. 중학교에는 고전적인 과목이 있다. (, 왜 나는 항상 중학교 과목을 사용한다.) 그것은 제품 합격률에 관한 것이다.

하지만 이 문제는 대부분의 경우, 우리에게 별 의미가 없습니다. 왜냐하면 실제로 우리는 제품의 평균 폐기물 비율이 얼마나 될지 모르기 때문입니다. 평균 폐기물 비율이 검출 기준보다 높다면, 우리 제품 한 무리가 검사를 통과할 확률은 얼마나 될까요? 만약 20,000개의 제품을 검출한다면, 10,000개의 제품의 결과를 직접적으로 사용할 수 있을까요?

중국 양적 투자 협회