마팅게일 전략, 운명의 도박?

마틴 전략과 피보나치 협동, 파지오드 간격과 배수와 같은 위험 요소를 동적으로 조정하는 것은 매우 깊이있는 연구의 가치가있는 연구 분야입니다.

이론적으로, 마틴겔 거래 전략의 매력은 당신이 충분한 자금을 가지고 있다면, 당신은 100 대 100을 이길 수 있다는 것입니다.

마틴의 거래 전략에 대해서는, 금융 투기 분야에서 100년 동안 가장 오래 지속된 거래 전략 중 하나입니다. 절차적 인 상장 및 상하, 미리 정확하게 측정 할 수있는 철회 및 이익, 진출 및 출구와 상관없이, 대부분의 상황 하에서 수천 군대를 횡단합니다.

마틴처럼 논쟁의 여지가 있는 거래 전략은 없습니다. 이득과 승리의 뒤에는 위험의 지수적 증폭과 치명적인 갑작스런 충격이 있습니다. 이 사건은 외환거래 플랫폼을 불안하게 만들고, 큰 돈의 전쟁과 칼의 전쟁, 그리고 수많은 전설을 남겼습니다.

• ### 1 간단한 초보자 마틴 전략

마틴 전략의 기본 원칙은 양측 시장에서 거래할 수 있고, 전체적으로 한쪽만 내기를 하고, 반대하면 계속 역으로 부가한다. 시장이 회수될 때까지, 이전의 모든 손실을 완전히 보상한다.

여기, 저는 가장 간단한 마틴 전략의 철회 성능을 점진적으로 수동으로 계산하여 여러분과 함께 평가할 것입니다.

예를 들어: “이런 일이 벌어진다면, 우리는 미국을 떠나서, 첫 번째 포지션 0.1 손. 매번 15점 간격으로 동등한 비율로 포지션을 추가한다. 점차는 1점으로 설정되어 있습니다. 계층은 20 계층으로 설정된다. 즉, 시장의 큰 일방적인 경우, 역동적 인 상장 20 배.

마틴의 가장 간단한 전략인 탈퇴를 분석해보자.

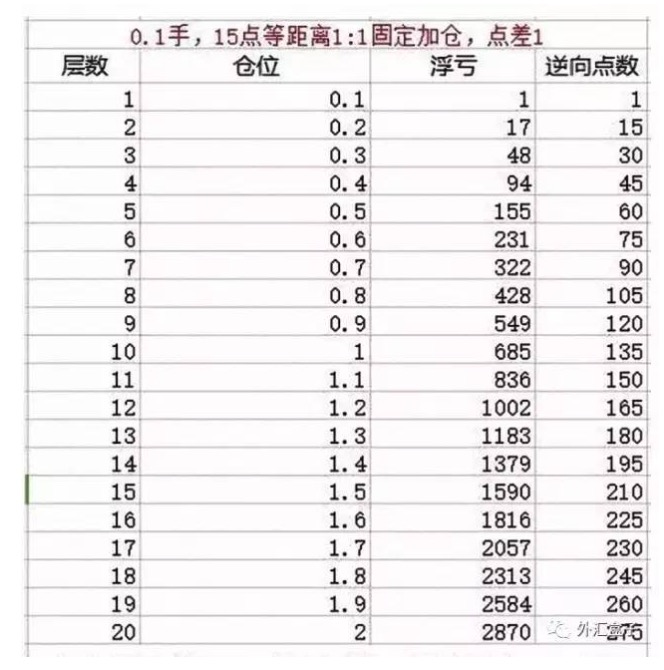
위 그림은 외환 초보자 중견 거래자들이 자주 사용하는 동거리의 역전도 거래 전략, 즉 우리가 흔히 말하는 역전도 마틴 전략이다.

포지션을 부풀린 거래자는 여러 계층의 반전적 포지션 증가를 저지한다.

우리는 20층에 도달했을 때, 포지션이 2개로 되어, 역전투자 275점, 2870달러의 상쇄 손실을 보게 됩니다. 상쇄 손실을 초기 상태로 되돌리려면, 143.5점을 되돌릴 필요가 있습니다.

만약 이 시점에 거래가 반향하지 않고 거래자가 계층을 늘리는 것을 멈추면, 우리는 계속해서 역동적으로 변할 위험을 측정할 수 있습니다.

400점의 단면 사각지대를 설정하여 한쪽을 400점으로 설정한다. 상위 20층의 역점 수는 275점이고, 단방의 역점은 125점이다.*20, 2870+2500=5370달러 2손의 포지션은 5370달러를 상환해야 하고, 260달러를 상환할 때까지 기다려야 한다. 이건 정말 엉뚱한 일이에요.

이것은 마틴의 가장 간단한 입문 전략입니다. 이 전략을 평가하면 20층의 가중치 상황에서 반발의 50%를 회수해야한다는 것을 알 수 있습니다. 실제로, 초강한 파동의 상황에서 50%의 빠른 회수는 거의 불가능하며, 이는 이 전략의 효율성을 떨어뜨릴 것입니다.

급속한 보완 속도를 높이기 위해, 같은 거리의 가축 상태에서, 역동의 후기에 포지션의 배수를 늘려야 합니다. 예를 들어, 1.5 배 또는 2 배의 포지션 비율에 따라 가축을 합니다. 그러나 그것은 포지션의 급격한 크기를 가져오며, 통제가 좋지 않으면, 부실이 급격히 가속화됩니다. 이것이 우리가 흔히 말하는 마틴의 잠재적인 위험이 매우 큰 이유입니다.

• ### 마틴의 전략의 여러 위험요소

우리는 마틴의 전략에 대해 더 깊이 연구할 수 있는 여러 변수들이 있음을 알 수 있습니다. 우리는 이것을 위험 요소라고 부릅니다.

초기 포지션: 이 영향은 그리 크지 않고, 선형적이고, 잘 측정되고, 계산된다.

포지션의 거리: 15점의 거리, 30점의 거리, 또는 일정 비율의 동적 거리 포지션으로 포지션이 추가되는 것은 마틴의 잠재적인 위험에 직접적으로 영향을 미칩니다. 이 요소가 동적 거리 포지션으로 변환되면, 예를 들어 피포나치 비율의 거리에 따라 역 포지션으로 계산하면 매우 복잡해집니다.

가증의 배수: 1:1의 비율로 가증, 또는 1:1.5 또는 1:2의 배수 가증, 또는 피보나치 비율에 따라 가증의 배수를 제어하는 것이 전체 포지션의 자리수와 계산의 복잡도에 직접 영향을 미칩니다.

이 중, 가장 거리 및 가장 곱수가 동적 곡선을 나타낼 때, 전체 계산 모형은 매우 복잡해진다. 마틴 전략의 동적 거리는 동적 포지션과 함께, 다양한 위험 곡선을 조정할 수 있다. 이것은 마틴 전략의 연구 개발의 핵심 초점이 되어야 하며, 컴퓨터 프로그래밍을 이용하여 계산을 더 잘 보조할 수 있다.

• ### 마틴의 전략은 수 많은 슈퍼 변종을 낳을 수 있습니다.

“이런 생각이 들었어요. 리스크를 방지하기 위해, 초기 포지션 위치를 선택하여 파장의 바닥에서 더 긴 공간을 선택할 수 있습니다. 예를 들어, 바닥에서 60점 상승한 후 역으로 공백을 시작하고 역으로 마틴의 위치를 점차적으로 증가시킵니다. 이렇게하면 가장 밑에 축적 된 몇 가지 위험 요소를 제거 할 수 있습니다.

은 마틴과 다른 기술 지표의 조합을 선택할 수 있습니다. 예를 들어 30, 60, 200 등 평행선 위치, 또는 브린 밴드의 오프라인 레일, 서로 다른 동적 마틴 포지션과 함께.

특정 위치에서, 마틴의 치명적인 피해를 줄이기 위해 전략적으로 동적으로 포지션을 상쇄할 수 있습니다. 포지션은 마틴 전략을 사용하여 포지션 상쇄를 할 수도 있습니다.

마틴 전략과 피보나치 협동은 매우 깊이 있는 연구 가치가 있는 과학 연구 영역이다. 각 요소에 대한 상세한 추론 계산을 잘 통제하면 슈퍼 마틴을 생성할 가능성이 있다.

[외환박스]