리크와 입찰-매도 스프레드: EKOP 모델에 대한 예비 연구

• #### 1 개략

요즘은 엄청 바빠서, 지난 글쓰기 몇 달이 지났어요. 지난 몇 달 동안 많은 일들이 일어났고, 그 중 일부는 내 인생에 있어서, 절대적으로 어두운 천둥이었습니다. 하지만 이 경험들은 저에게 말해줬어요. 인생은 거래와 마찬가지로, 오르락 내리락, 미지의 것들로 가득 차 있습니다. 우리는 항상 이미 일어난 일들로부터 무언가를 배우고, 서서히 존재하지 않을지도 모르는 진실에 가까워지기를 바랍니다.

우리는 모두 거래가 활발한 주식은 일반적으로 비교적 작은 매매 가격 차이를 ((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((([1] 처음에 제안한 것은, 서로 다른 정보를 가진 거래자의 행동이, 이 두 종류의 주식 가격 차이가 존재하는 이유를 연구하기 위해서였다. 이 칼럼 기사에서, 나는 이 모델의 기초를 소개할 것이다. 모델의 응용은, 후속 기사에서 (내가 시간이 있다면) 더 나아가 분석할 것이다.

• #### 2 거래 과정의 가정

우리가 금융 모델에 대해 이야기 할 때, 가장 중요한 것은 이 모델의 가정에 주의를 기울이는 것입니다. 좋은 금융 모델은 나름대로의 가정이 있습니다: 그것은 보편성이 없을 정도로 너무 강하지 않을 것입니다. 그것은 아름답고 간결한 결과를 도출 할 수 없을 정도로 너무 약하지 않을 것입니다. EKOP 모델의 기본 가정은 다음과 같습니다:

가정 1: 우리는 주식 거래에 대해 이야기하고 있으며, 거래 행위는 하루 동안 분산되고, 하루 동안 연속되어 있다고 가정합니다. 즉, 거래자의 거래 행위는 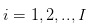분산된 거래 날 중 /upload/asset/57926eb5a1e7fa14063c4148b25499190bfa6919.png에서 이루어집니다. 거래 당일에는 /upload/asset/57926eb5a1e7fa14063c4148b25499190bfa6919.png에서 거래가 이루어집니다.

• 나쁜 소식은, 우리는 주식의 가치를 /upload/asset/8f720dc4498bef072905f36716329fb91b93041f.png로 기록했습니다.
• 좋은 소식이 있습니다.
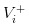
• 어떤 소식도 없었고, 우리는 주식의 가치를 /upload/asset/dc0a1719b4fa5eaef9356473496f1bb70c3d98a6.png로 기록했습니다.

우리는 분명히 /upload/asset/6487043d156510fd43080526c4b2fef3850e99d4.png를 가지고 있습니다.

가설 2: 어느 날,

주식 가격에 영향을 미치는 사건의 발생 확률은 1 -α, 주식 가격에 영향을 미치지 않는 사건의 발생 확률은 1 -α이다. 사건이 일어난 날에는 주식 가격을 떨어뜨리는 나쁜 일이 일어날 확률이 1 -δ, 주식 가격을 올리는 좋은 일이 일어날 확률이 1 -δ이다.

가설 3: 주식 거래의 참가자는 시장 메이커 (market maker, 약자 MM), 정보 상인 (informed trader, 약자 IT), 정보 상인이 아닌 거래자 (uninformed trader, 약자 UT) 로 구성되어 있다. 그들은 각각 다음과 같은 거래 행동을 따르고 있다.

MM는 항상 한 단위의 구매 또는 판매 주문을 할 준비가되어 있으며, 시장 사업자의 의무가 있습니다. MM는 위험 중립적이며, 따라서 그는 자신이 생각하는 공정한 가격으로 주문합니다.

IT는 뉴스가 있는 날만 거래하고, 그들의 거래행위는 느긋한 과정이다. 어느 날, 나쁜 뉴스가 있는 날, 그는 μ의 도착률 (arrival rate) 으로 판매권을 붙인다. 좋은 뉴스가 있는 날에는 μ의 도착률으로 구매권을 붙인다.

UT, 즉 우리의 불쌍한 菜, 소식이 없는 장점 때문에, 그들의 거래 행위는 매일, 도착률에 따라 구매와 판매의 표를 올리는 松 과정이기도 합니다. 참고로, 여기 모든 포슨 과정은 서로 독립적이다. 우리는 가설 3을 하나의 도표로 나타낼 수 있다.

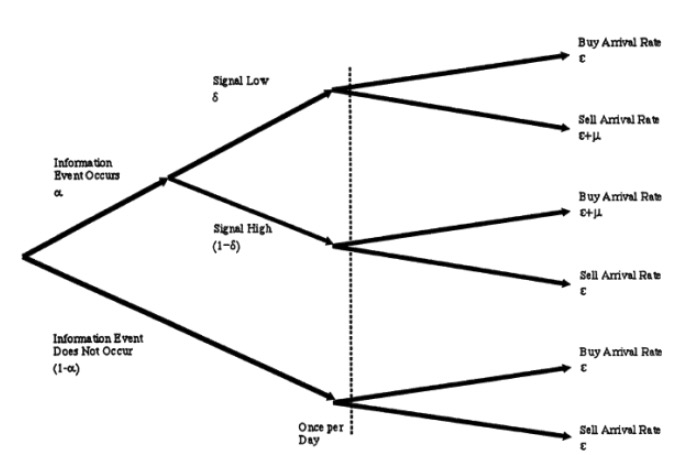
• #### 3 거래 및 가격 업데이트

우리가 알고 있는 바와 같이, 시장거래자는 보통 거대 기업을 위해 일하고 있습니다. 그들은 매우 똑똑합니다. 그들은 IT와 UT와 오랜 기간 동안 싸웠고, 그들은 많은 역사적 데이터 분석을 통해 위의 트리그램의 모든 모델 변수를 정리했습니다. 그러나 다행스럽게도, 그들은 정보 상인만큼 강하지 않습니다. 거래가 시작될 때, 그들은 거래가 시작될 때, 그들은 거래가 시작될 때, 오늘 무슨 일이 있었는지에 대해 상인처럼 알지 못합니다. 그들이 할 수 있는 것은, 거래가 진행되는 동안, 다른 거래자의 보고서를 통해 계속해서 업데이트하는 것입니다. 오늘 무슨 일이 있었는지, 좋은 일이었는지 나쁜 일이었는지에 대한 자신의 추측을 계속하는 것입니다.

자, 이제 MM의 역할을 경험해 보겠습니다. IT와 UT와 싸워보죠. 어떤 시점 t에서 우리는 우리 자신을 어떤 일이 일어날 확률에 대한 벡터로 기록합니다.

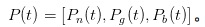。 분명히, 하루가 막 시작되었을 때, 즉 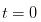때, 나는 보고서를 한 장도 보지 않았기 때문에 내가 할 수 있는 것은 아무 일도 일어나지 않을 확률이 α이고, 좋은 일이 일어날 확률은 /upload/asset/c9cf50c6146a25c662c593ed229845822bfac7a5.png이며, 나쁜 일이 일어날 확률은 /upload/asset/87418f07b12fce65f4c3f70b024e94d2e19f769a.png입니다.

그럼 어떻게 이 확률을 업데이트해야 할까요? 자, 우리 중 시장선택을 하는 사람들은 모두 베이스 공식을 알고 있습니다. 우리는 베이스 법칙을 이용해서 판매가 된 것을 관찰하고, 우리의 확률 추정치를 업데이트합니다. 우리는 오늘 소식이 없는 확률 추정치를 업데이트합니다.

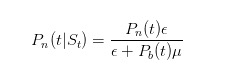
이 공식의 분자는, 소식이 없을 때, 모르는 거래자만이 ε 밑으로 상할 것이라고 말하고, 분모는, 아무 때나 모르는 거래자는 ε 밑으로 상할 것이라고 말하고, 아는 거래자는 나쁜 일이 일어날 때만 μ 밑으로 상할 것이라고 말하고 있다. 비슷하게, 우리는 추론할 수 있다

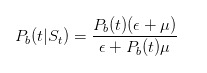
그리고

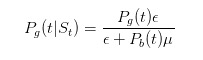
우리가 추론을 진행하기 전에, 간단한 테스트를 해봅시다. 방금 우리가 판매요금을 보았을 때, 우리는 나쁜 일이 일어날 확률을 높여야 한다고 말했습니다.

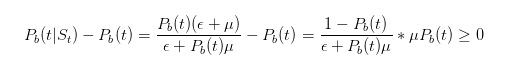
그리고, 우리의 추론은 우리의 직관과 일치합니다.

이 확률이 업데이트된 후, 우리는 시장에서 내놓은 구매 가격으로 정의할 수 있습니다.

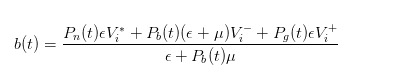
비슷한 추론을 통해, 우리는 구매자가 오면, 우리가 시장에서 판매자로서 보고하는 판매가격은

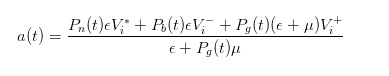
• #### 4 가격의 변화 후의 가격 차차 표현식

위의 구매 가격과 판매 가격의 표현은 충분히 직관적이지 않습니다. 우리는 t 시점의 주식의 기대 가치를 도입하여 표현을 간소화 할 수 있습니다.

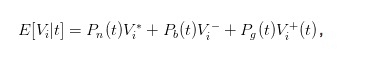
그래서 우리는 bid와 ask의 표현을

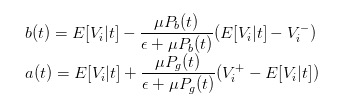
그래서 우리는 가격 차이를 명확하게 표현할 수 있습니다

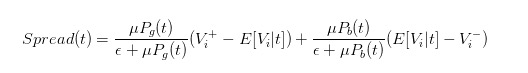
• #### 5 거래자의 행동으로 인한 가격차이의 영향

가격차이의 표현을 가지고, 우리는 가격차이에 대한 다른 거래자의 영향을 분석할 수 있습니다!

菜가 많을수록, 가격차가 작아진다. 주의할 점은, ε는 무지한 거래자 (菜라고 부르자) 의 도달률이며, ε >> μ가 있으면, 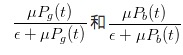둘 다 0으로 나아갈 것이고, 이는 스프레드 또한 0으로 나아갈 것을 의미한다. 만약 우리가 또 다른 극단으로 가서, 시장에 이 없다고 가정하고, 보다 더 나은 정보 거래자만 있다고 가정한다면, 우리는 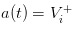및 /upload/asset/1248ca7d3d472490982c9d0aa7b2e04b51269b18.png의 가격으로 상장할 것을 알게 될 것입니다. 따라서 정보 거래자는 매매가 수익성이 없다는 것을 알게 될 것입니다.

우리가 몇 가지 가설을 바탕으로 아주 간단한 수학적 추론을 이용해서 이렇게 재미있고 심오한 결론을 내릴 수 있다는 것은 아마도 수학 모델의 큰 매력일 것이다. 이 글을 읽고 난 뒤, 저는 여러분들이 菜를 잘 대하길 바랍니다. 우리 菜는 시장이 정상적으로 거래할 수 있도록 보장하는 것입니다!

[1] Easley, David, et al. “Liquidity, information, and infrequently traded stocks.” The Journal of Finance 51.4 (1996): 1405-1436.