고빈도 트레이딩 전략에 대한 생각 (1)
 3
3
 4856
4856

본 논문에서는 디지털 통화의 고빈도 거래 전략, 수익 원천(주로 시장 변동과 거래소 수수료 할인), 주문 실행 및 포지션 제어 문제, 파레토 분포를 이용한 거래량 모델링 방법 등에 대해 논의합니다. 또한, 바이낸스가 제공하는 거래 및 최적 주문 데이터는 백테스팅에 활용되었으며, 고빈도 트레이딩 전략의 다른 이슈들은 후속 기사에서 심도 있게 논의될 예정입니다.
저는 이전에 디지털 통화의 고빈도 거래에 관해 두 편의 기사를 썼습니다. 디지털 통화를 위한 고빈도 전략에 대한 자세한 소개, 5일만에 80배 벌기, 고빈도 전략의 힘. 하지만 이는 단지 경험의 공유이자 일반적인 대화로 간주될 수 있습니다. 이번에는 고빈도 트레이딩의 아이디어를 처음부터 소개하는 일련의 기사를 쓸 계획입니다. 가능한 한 간결하고 명확하게 작성하고자 합니다. 하지만 고빈도 트레이딩에 대한 제 제한된 수준과 심층적인 이해로 인해 거래, 이 글은 단지 시작점일 뿐입니다. 전문가가 저를 바로잡아 주셨으면 좋겠습니다.
고빈도 수익원
이전 기사에서 언급했듯이, 고빈도 전략은 극도로 변동성이 큰 상승과 하락이 있는 시장에 특히 적합합니다. 전반적인 추세와 변동을 포함하여 단기간에 걸친 거래 상품의 가격 변화를 살펴봅니다. 우리가 추세의 변화를 정확하게 예측할 수 있다면, 우리는 확실히 돈을 벌 수 있지만, 이것이 가장 어려운 일이기도 합니다. 이 글은 주로 고빈도 메이커 전략을 소개하며, 이 문제는 다루지 않을 것입니다. 변동성이 큰 시장에서 상승과 하락 주문을 하는 전략을 충분히 자주 실행하고 이익 마진이 충분히 크다면 추세로 인해 발생할 수 있는 손실을 커버할 수 있으므로, 시장을 예측하지 않고도 수익을 낼 수 있습니다. 현재 거래소의 모든 메이커 거래는 거래 수수료에 대한 리베이트를 받는데, 이는 또한 이익의 구성 요소입니다. 경쟁이 치열할수록 리베이트 비중이 높아야 합니다.
해결해야 할 문제
이 전략은 매수 주문과 매도 주문을 동시에 내는 것입니다. 첫 번째 질문은 어디에 주문을 내야 하는가입니다. 주문이 시장에 가까울수록 거래 가능성이 높아집니다. 그러나 변동성이 큰 시장에서는 즉각적인 거래 가격이 시장에서 멀리 떨어져 있을 수 있습니다. 주문이 너무 가까이 배치되면 거래할 수 없습니다. 충분한 이익을 얻으세요. 너무 멀리 떨어진 곳에서 주문이 실행될 확률은 낮습니다. 이는 최적화가 필요한 문제입니다.
자신의 위치를 제어하세요. 위험을 통제하기 위해서는 장기간 너무 많은 포지션을 축적하는 전략은 바람직하지 않습니다. 이는 주문 간격, 주문 수량, 총 포지션 한도 등을 제어하면 해결할 수 있습니다.
위의 목표를 달성하기 위해서는 거래 확률, 거래 이익, 시장 추정 및 기타 측면을 모델링하고 추정하는 것이 필요합니다. 이 분야에는 많은 기사와 논문이 있으며, High-Frequency Trading과 같은 키워드로 찾을 수 있습니다. , 주문서 등 온라인에는 많은 추천 사항이 있지만 여기서는 설명하지 않겠습니다. 또한 신뢰할 수 있고 빠른 백테스팅 시스템을 구축하는 것이 가장 좋습니다. 고빈도 전략은 실제 거래를 통해 효과를 검증하기 위해 쉽게 검증할 수 있지만, 백테스팅은 여전히 더 많은 아이디어를 제공하고 시행착오 비용을 줄일 수 있습니다.
필수 데이터
바이낸스는 거래별 데이터와 최상 주문 데이터를 제공합니다.다운로드심층 데이터는 허용 목록에 있는 API를 사용하여 다운로드해야 하며, 직접 수집할 수도 있습니다. 백테스팅 목적으로는 수집된 거래 데이터만 사용할 수 있습니다. 이 기사에서는 HOOKUSDT-aggTrades-2023-01-27의 데이터를 예로 들어보겠습니다.
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
거래 열은 다음과 같습니다.
- agg_trade_id: 집계된 거래 주문의 ID
- 가격 : 거래가격
- 수량 : 거래 건수
- first_trade_id: 컬렉션에 동시에 여러 거래가 있을 수 있으며, 데이터는 하나만 계산됩니다. 이는 첫 번째 거래의 ID입니다.
- last_trade_id: 마지막 거래의 id
- transact_time: 거래 시간
- is_buyer_maker: 거래 방향, True는 매수 주문이 메이커에 의해 거래되고 매도 주문이 테이커에 의해 거래됨을 의미합니다.
해당 날짜에 거래 데이터가 66만 건이 있었고, 거래가 매우 활발했던 것을 알 수 있습니다. csv는 댓글 섹션에 첨부하겠습니다.
trades = pd.read_csv('COMPUSDT-aggTrades-2023-07-02.csv')
trades
664475 rows × 7 columns
| agg_trade_id | price | quantity | first_trade_id | last_trade_id | transact_time | is_buyer_maker |
|---|---|---|---|---|---|---|
| 120719552 | 52.42 | 22.087 | 207862988 | 207862990 | 1688256004603 | False |
| 120719553 | 52.41 | 29.314 | 207862991 | 207863002 | 1688256004623 | True |
| 120719554 | 52.42 | 0.945 | 207863003 | 207863003 | 1688256004678 | False |
| 120719555 | 52.41 | 13.534 | 207863004 | 207863006 | 1688256004680 | True |
| … | … | … | … | … | … | … |
| 121384024 | 68.29 | 10.065 | 210364899 | 210364905 | 1688342399863 | False |
| 121384025 | 68.30 | 7.078 | 210364906 | 210364908 | 1688342399948 | False |
| 121384026 | 68.29 | 7.622 | 210364909 | 210364911 | 1688342399979 | True |
단일 거래량 모델링
먼저, 데이터를 처리하고 원래 거래를 매수 주문 활성 거래 그룹과 매도 주문 활성 거래 그룹으로 나눕니다. 또한 원래 집계된 거래 데이터는 동일한 시간, 동일한 가격, 동일한 방향의 데이터입니다. 100개의 활성 매수 주문이 있을 수 있습니다. 가격이 다른 여러 거래로 분할된 경우, 60과 40으로, 두 가지 데이터가 생성되어 매수 주문량 추정에 영향을 미칩니다. 따라서 transact_time을 기준으로 다시 집계하는 것이 필요합니다. 집계 후 데이터 양이 14만 건 줄었습니다.
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
sell_trades = trades[trades['is_buyer_maker']==True].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
sell_trades = sell_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
sell_trades['interval']=sell_trades['transact_time'] - sell_trades['transact_time'].shift()
print(trades.shape[0] - (buy_trades.shape[0]+sell_trades.shape[0]))
146181
매수 주문을 예로 들어, 먼저 히스토그램을 그립니다. 롱테일 효과가 매우 명백하다는 것을 알 수 있습니다. 대부분의 데이터는 맨 왼쪽에 집중되어 있지만, 꼬리 부분에 분산된 소수의 대규모 거래도 있습니다. .
buy_trades['quantity'].plot.hist(bins=200,figsize=(10, 5));
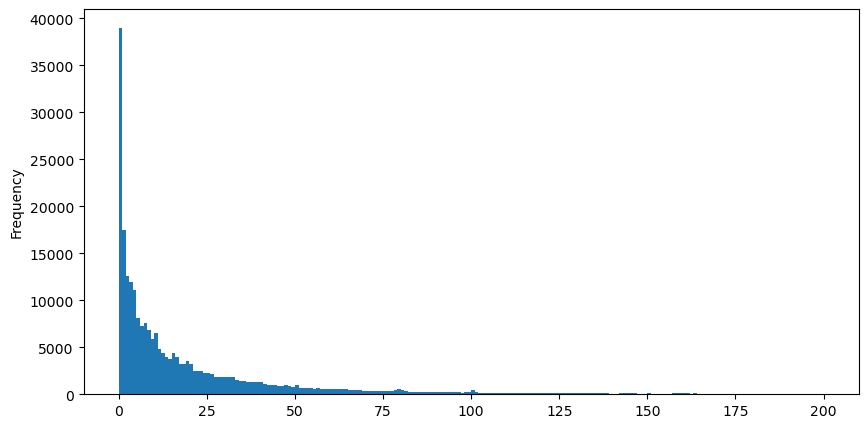
관찰의 편의를 위해 꼬리 부분을 잘라내어 관찰합니다. 거래량이 클수록 발생 빈도가 낮아지고 감소 추세가 더 빠른 것을 알 수 있습니다.
buy_trades['quantity'][buy_trades['quantity']<200].plot.hist(bins=200,figsize=(10, 5));
볼륨 만족도 분포에 대한 연구는 많이 있다. 그 거듭제곱 법칙 분포는 파레토 분포라고도 불리며, 통계 물리학과 사회 과학에서 일반적인 확률 분포 형태입니다. 거듭제곱 법칙 분포에서 특정 크기(또는 빈도)의 사건의 확률은 해당 사건 크기의 음의 지수에 비례합니다. 이 분포 형태의 주요 특징은 큰 사건(즉, 평균에서 멀리 떨어진 사건)이 다른 여러 분포에서 예상되는 것보다 더 자주 발생한다는 것입니다. 이는 거래량 분포의 특징이다. 파레토 분포의 형태는 P(x) = Cx^(-α)입니다. 다음은 이를 보여주는 것입니다.
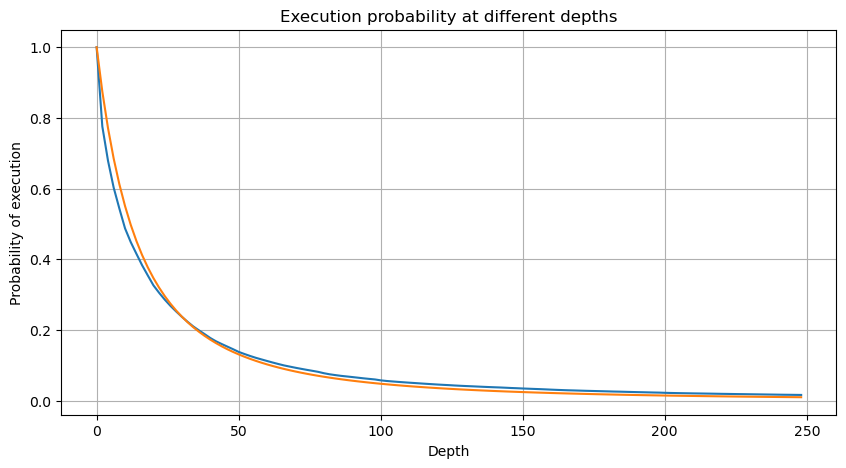
아래 그림은 거래량이 특정 값보다 클 확률을 보여줍니다. 파란색 선은 실제 확률이고 주황색 선은 시뮬레이션된 확률입니다. 여기서 특정 매개변수에 대해 걱정하지 마십시오. 파레토 분포를 만족한다. 주문량이 0보다 클 확률은 1이고, 표준화 요구 사항을 충족하기 위해 분포 방정식은 다음과 같아야 합니다.
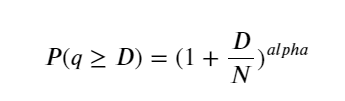
여기서 N은 표준화된 매개변수입니다. 여기서는 평균 볼륨 M과 알파 -2.06을 선택합니다. 알파의 구체적인 추정치는 D=N일 때 P 값을 역으로 계산하여 계산할 수 있습니다. 구체적으로: 알파 = log(P(d>M))/log(2). 다른 지점을 선택하면 알파 값이 약간씩 달라집니다.
depths = range(0, 250, 2)
probabilities = np.array([np.mean(buy_trades['quantity'] > depth) for depth in depths])
alpha = np.log(np.mean(buy_trades['quantity'] > mean_quantity))/np.log(2)
mean_quantity = buy_trades['quantity'].mean()
probabilities_s = np.array([(1+depth/mean_quantity)**alpha for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
plt.figure(figsize=(10, 5))
plt.grid(True)
plt.title('Diff')
plt.plot(depths, probabilities_s-probabilities);
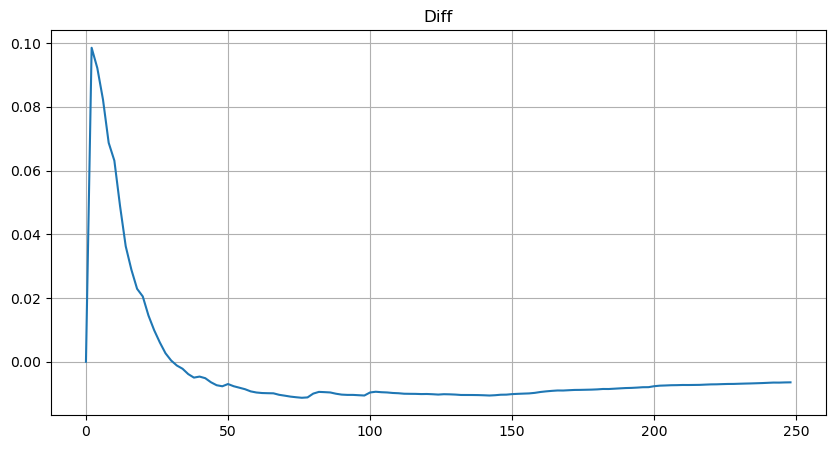
하지만 이 추정치는 그렇게 보일 뿐입니다. 위의 그림에서 우리는 시뮬레이션된 값과 실제 값의 차이를 그래프로 표시합니다. 거래량이 적을 때는 편차가 크며, 10%에 가까울 때도 있습니다. 매개변수 추정 중에 다양한 점을 선택하면 점의 확률을 더 정확하게 만들 수 있지만, 이렇게 해도 편차 문제는 해결되지 않습니다. 이는 power-law 분포와 실제 분포의 차이에 의해 결정됩니다. 더 정확한 결과를 얻으려면 power-law 분포의 방정식을 수정해야 합니다. 구체적인 과정에 대해서는 자세히 설명하지 않겠지만, 갑자기 영감이 떠올랐고 실제로는 다음과 같은 과정이 필요하다는 걸 알게 됐습니다.
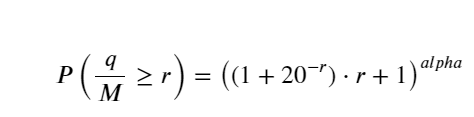
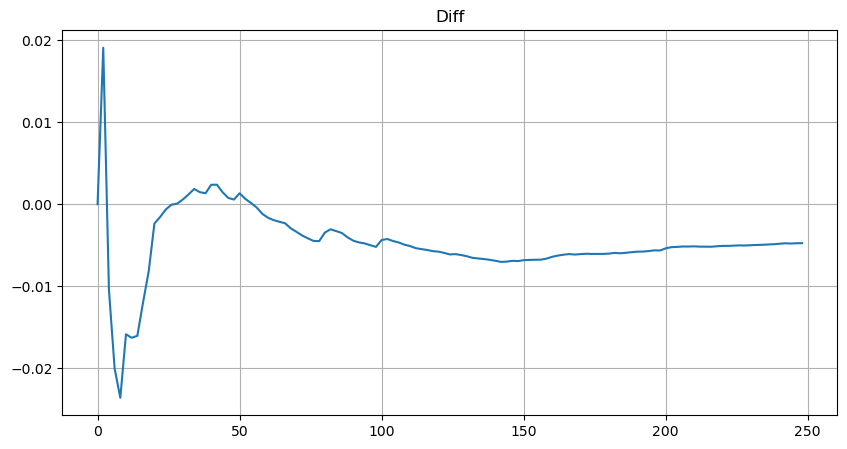
단순화를 위해 여기서는 r = q/M을 사용하여 표준화된 거래량을 나타냅니다. 매개변수는 위와 같은 방식으로 추정할 수 있습니다. 아래 그림은 교정 후 최대 편차가 2%를 넘지 않음을 보여줍니다. 이론적으로는 교정을 계속할 수 있지만 이 정확도로 충분합니다.
depths = range(0, 250, 2)
probabilities = np.array([np.mean(buy_trades['quantity'] > depth) for depth in depths])
mean = buy_trades['quantity'].mean()
alpha = np.log(np.mean(buy_trades['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([(((1+20**(-depth/mean))*depth+mean)/mean)**alpha for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
plt.figure(figsize=(10, 5))
plt.grid(True)
plt.title('Diff')
plt.plot(depths, probabilities_s-probabilities);
부피 분포에 대한 추정 방정식에서 방정식의 확률은 실제 확률이 아니라 조건부 확률이라는 점에 유의하세요. 이 시점에서 우리는 다음 질문에 답할 수 있습니다. 다음 순서가 발생한다면, 이 순서가 특정 값보다 클 확률은 얼마입니까? 다시 말해, 서로 다른 깊이의 주문이 실행될 확률은 얼마인가(이상적인 상황이고 그렇게 엄격하지는 않음, 이론상 주문장에는 새로운 주문과 취소가 있고, 같은 깊이에 대기열이 있음).
이 기사는 여기서 거의 끝났고, 여전히 답해야 할 질문이 많이 있습니다. 다음 시리즈의 기사에서는 답을 제공하려고 노력할 것입니다.