고빈도 트레이딩 전략에 대한 생각 (3)
 0
0
 2664
2664

이전 글에서는 누적 거래량을 모델링하는 방법을 소개하고, 가격 충격 현상을 간략하게 분석했습니다. 이 기사에서는 거래 주문 데이터를 계속해서 분석하겠습니다. 지난 이틀 동안 YGG가 Binance U 기반 계약을 출시했고, 가격이 크게 변동했고, 거래량은 한때 BTC를 넘어섰습니다. 오늘 분석해 보겠습니다.
주문 시간 간격
일반적으로 주문이 도착하는 시간은 포아송 과정을 따른다고 가정합니다. 다음은 이를 소개하는 기사입니다.푸아송 과정 . 아래에서 이를 보여드리겠습니다.
8월 5일에 aggTrades를 다운로드하면 총 1,931,193건의 거래가 이루어지는데, 이는 상당히 과장된 수치입니다. 먼저 매수 주문의 분포를 살펴보겠습니다. 100ms와 500ms 부근에서 불균일한 지역적 피크가 있는 것을 볼 수 있습니다. 이는 Iceberg가 위탁한 로봇이 예약한 주문으로 인해 발생해야 합니다. 또한 다음 중 하나일 수 있습니다. 그날 시장 상황이 특이했던 이유 중 하나입니다.
푸아송 분포의 확률 질량 함수(PMF)는 다음과 같습니다.
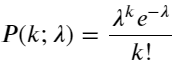
안에:
- k는 우리가 관심을 갖고 있는 사건의 수입니다.
- λ는 단위 시간(또는 단위 공간)당 사건의 평균 발생률입니다.
- P(k; λ)는 평균 발생률 λ가 주어졌을 때 정확히 k개의 사건이 발생할 확률입니다.
푸아송 과정에서 사건 간의 시간 간격은 지수 분포를 따릅니다. 지수 분포의 확률 밀도 함수(PDF)는 다음과 같습니다.
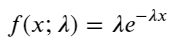
피팅을 통해, 결과가 포아송 분포의 예상 결과와 상당히 다르다는 것을 발견했습니다. 포아송 프로세스는 긴 간격의 빈도를 과소평가하고 짧은 간격의 빈도를 과대평가했습니다. (실제 구간 분포는 수정된 파레토 분포에 더 가깝습니다)
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
trades = pd.read_csv('YGGUSDT-aggTrades-2023-08-05.csv')
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
buy_trades.index = buy_trades['date']
buy_trades['interval'][buy_trades['interval']<1000].plot.hist(bins=200,figsize=(10, 5));
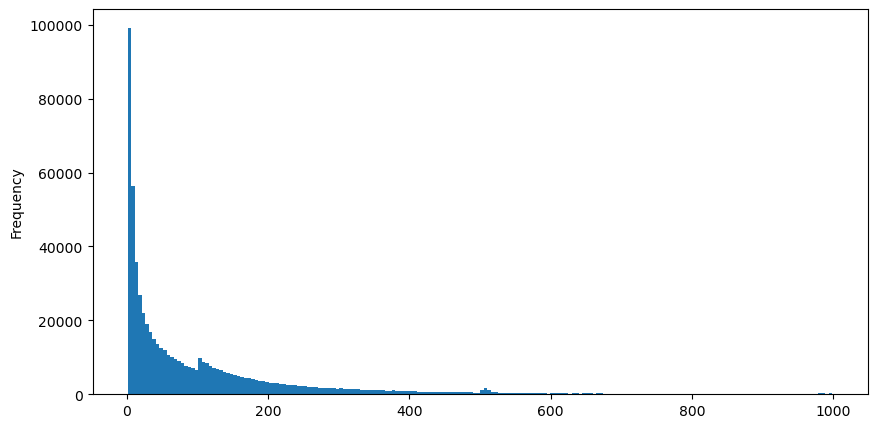
Intervals = np.array(range(0, 1000, 5))
mean_intervals = buy_trades['interval'].mean()
buy_rates = 1000/mean_intervals
probabilities = np.array([np.mean(buy_trades['interval'] > interval) for interval in Intervals])
probabilities_s = np.array([np.e**(-buy_rates*interval/1000) for interval in Intervals])
plt.figure(figsize=(10, 5))
plt.plot(Intervals, probabilities)
plt.plot(Intervals, probabilities_s)
plt.xlabel('Intervals')
plt.ylabel('Probability')
plt.grid(True)
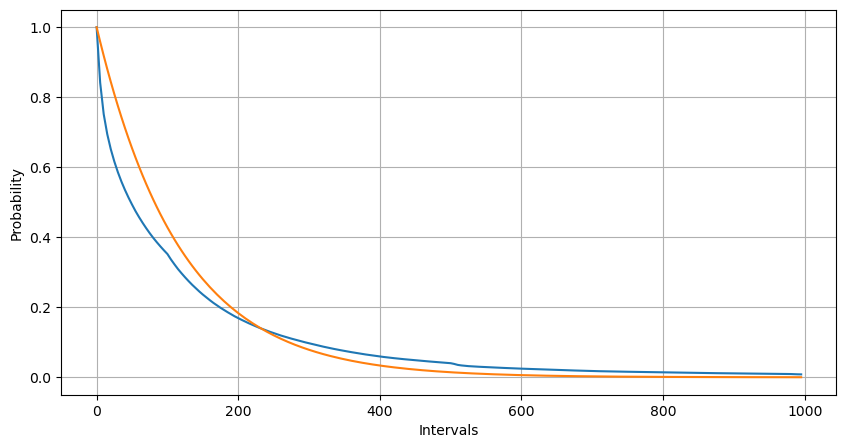
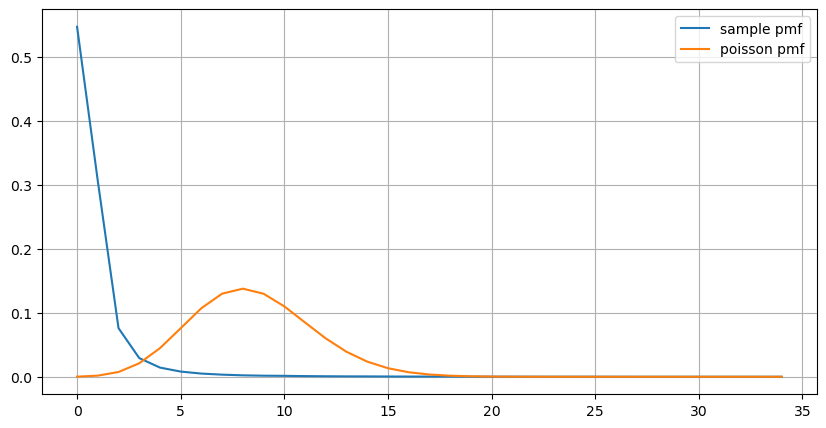
1초 안에 발생하는 주문 수의 통계적 분포를 포아송 분포와 비교해도 매우 확실한 차이가 있음을 알 수 있습니다. 푸아송 분포는 확률이 낮은 사건의 빈도를 상당히 과소평가합니다. 가능한 원인:
- 발생 속도가 일정하지 않음: 포아송 과정은 주어진 기간 동안 발생하는 사건의 평균 속도가 일정하다고 가정합니다. 이 가정이 적용되지 않으면 데이터 분포는 포아송 분포에서 벗어나게 됩니다.
- 과정의 상호작용: 포아송 과정의 또 다른 기본 가정은 사건이 서로 독립적이라는 것입니다. 실제 세계의 사건들이 서로 영향을 미치는 경우, 사건들의 분포는 푸아송 분포에서 벗어날 수 있습니다.
즉, 실제 환경에서는 주문 빈도가 일정하지 않고 실시간으로 업데이트되어야 하며, 고정된 시간 내에 더 많은 주문이 발생하면 더 많은 주문이 유도되는 인센티브가 발생합니다. 이로 인해 전략에서 단일 매개변수를 수정하는 것이 불가능해집니다.
result_df = buy_trades.resample('0.1S').agg({
'price': 'count',
'quantity': 'sum'
}).rename(columns={'price': 'order_count', 'quantity': 'quantity_sum'})
count_df = result_df['order_count'].value_counts().sort_index()[result_df['order_count'].value_counts()>20]
(count_df/count_df.sum()).plot(figsize=(10,5),grid=True,label='sample pmf');
from scipy.stats import poisson
prob_values = poisson.pmf(count_df.index, 1000/mean_intervals)
plt.plot(count_df.index, prob_values,label='poisson pmf');
plt.legend() ;
실시간 업데이트 매개변수
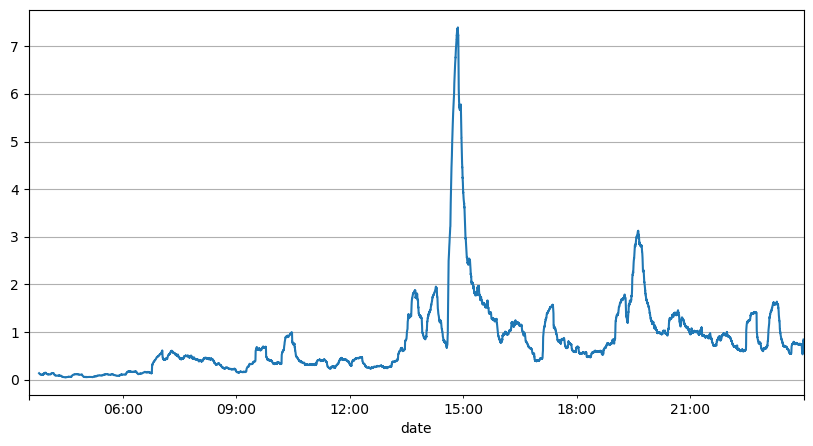
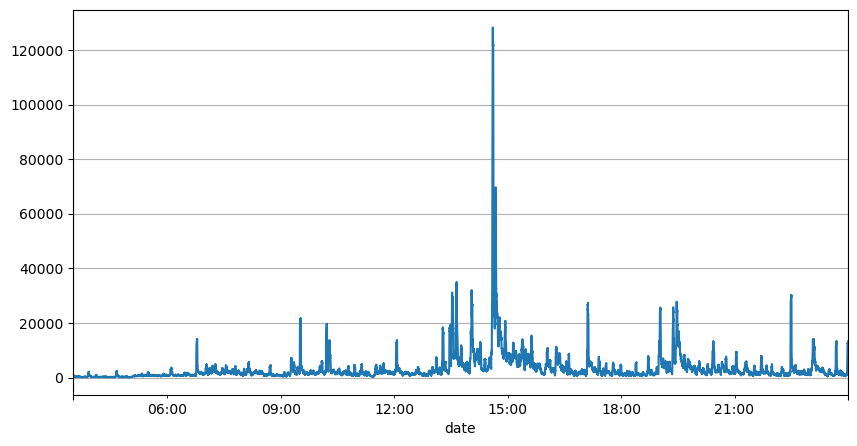
이전 주문 간격 분석을 통해 우리는 고정된 매개변수가 실제 시장 상황에 적합하지 않으며, 전략의 시장 설명에 대한 주요 매개변수는 실시간으로 업데이트되어야 한다는 결론을 내릴 수 있습니다. 가장 쉬운 해결책은 슬라이딩 윈도우의 이동 평균입니다. 아래 두 수치는 1초 내 매수 주문 빈도와 1000개의 거래량 윈도우 평균입니다. 거래에서 클러스터링 현상이 있는 것을 알 수 있습니다. 즉, 주문 빈도가 평소보다 상당히 높습니다. 시간이 지나면서 볼륨도 동시에 증가합니다. 여기서 이전 평균은 최신 초의 값을 예측하는 데 사용되고, 잔차의 평균 절대 오차는 예측의 품질을 측정하는 데 사용됩니다.
그래프에서 우리는 또한 주문 빈도가 포아송 분포에서 왜 그렇게 많이 벗어나는지 이해할 수 있습니다. 초당 평균 주문 수는 8.5배에 불과하지만 극단적인 경우 초당 평균 주문 수는 그것과 크게 벗어납니다.
여기서는 이전 2초의 평균을 사용하여 잔여 오차를 예측하는 것이 가장 작고 단순 평균 예측 결과보다 훨씬 더 나은 것으로 나타났습니다.
result_df['order_count'][::10].rolling(1000).mean().plot(figsize=(10,5),grid=True);
result_df
| order_count | quantity_sum | |
|---|---|---|
| 2023-08-05 03:30:06.100 | 1 | 76.0 |
| 2023-08-05 03:30:06.200 | 0 | 0.0 |
| 2023-08-05 03:30:06.300 | 0 | 0.0 |
| 2023-08-05 03:30:06.400 | 1 | 416.0 |
| 2023-08-05 03:30:06.500 | 0 | 0.0 |
| … | … | … |
| 2023-08-05 23:59:59.500 | 3 | 9238.0 |
| 2023-08-05 23:59:59.600 | 0 | 0.0 |
| 2023-08-05 23:59:59.700 | 1 | 3981.0 |
| 2023-08-05 23:59:59.800 | 0 | 0.0 |
| 2023-08-05 23:59:59.900 | 2 | 534.0 |
result_df['quantity_sum'].rolling(1000).mean().plot(figsize=(10,5),grid=True);
(result_df['order_count'] - result_df['mean_count'].mean()).abs().mean()
6.985628185332997
result_df['mean_count'] = result_df['order_count'].ewm(alpha=0.11, adjust=False).mean()
(result_df['order_count'] - result_df['mean_count'].shift()).abs().mean()
0.6727616961866929
result_df['mean_quantity'] = result_df['quantity_sum'].ewm(alpha=0.1, adjust=False).mean()
(result_df['quantity_sum'] - result_df['mean_quantity'].shift()).abs().mean()
4180.171479076811
요약하다
이 글에서는 순서 시간 간격이 포아송 과정에서 벗어나는 이유를 간략하게 소개합니다. 그 이유는 주로 매개변수가 시간이 지남에 따라 변하기 때문입니다. 시장을 더 정확하게 예측하려면 전략에서 시장의 기본 매개변수에 대한 실시간 예측을 해야 합니다. 잔차는 예측의 질을 측정하는 데 사용할 수 있습니다. 위의 예는 가장 간단한 예입니다. 시계열 분석, 변동성 집계 등에 대한 관련 연구가 많이 있으며, 이를 더욱 개선할 수 있습니다.