이전 기사에서는 다양한 중간 가격의 계산 방법에 대한 예비 소개를 제공하고 중간 가격의 개정을 제공했습니다. 이 기사에서는 이 주제를 계속 탐구합니다.

필수 데이터

실제 거래에서 주문 흐름 데이터와 10단계의 심도 데이터가 수집되었으며, 업데이트 빈도는 100ms입니다. 실제 시장은 매수 및 매도 데이터만 포함하고 있으며, 이는 실시간으로 업데이트됩니다. 단순성을 위해 당장은 사용하지 않습니다. 데이터가 너무 크다는 점을 고려하여 심층적인 데이터 행 10만 개만 보존하고, 각 레벨의 시장 상황도 별도의 열로 구분했습니다.

from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import ast
%matplotlib inline

tick_size = 0.0001

trades = pd.read_csv('YGGUSDT_aggTrade.csv',names=['type','event_time', 'agg_trade_id','symbol', 'price', 'quantity', 'first_trade_id', 'last_trade_id',
       'transact_time', 'is_buyer_maker'])

trades = trades.groupby(['transact_time','is_buyer_maker']).agg({
    'transact_time':'last',
    'agg_trade_id': 'last',
    'price': 'first',
    'quantity': 'sum',
    'first_trade_id': 'first',
    'last_trade_id': 'last',
    'is_buyer_maker': 'last',
})

trades.index = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index.rename('time', inplace=True)
trades['interval'] = trades['transact_time'] - trades['transact_time'].shift()

depths = pd.read_csv('YGGUSDT_depth.csv',names=['type','event_time', 'transact_time','symbol', 'u1', 'u2', 'u3', 'bids','asks'])

depths = depths.iloc[:100000]

depths['bids'] = depths['bids'].apply(ast.literal_eval).copy()
depths['asks'] = depths['asks'].apply(ast.literal_eval).copy()

def expand_bid(bid_data):
    expanded = {}
    for j, (price, quantity) in enumerate(bid_data):
        expanded[f'bid_{j}_price'] = float(price)
        expanded[f'bid_{j}_quantity'] = float(quantity)
    return pd.Series(expanded)
def expand_ask(ask_data):
    expanded = {}
    for j, (price, quantity) in enumerate(ask_data):
        expanded[f'ask_{j}_price'] = float(price)
        expanded[f'ask_{j}_quantity'] = float(quantity)
    return pd.Series(expanded)
# 应用到每一行，得到新的df
expanded_df_bid = depths['bids'].apply(expand_bid)
expanded_df_ask = depths['asks'].apply(expand_ask)
# 在原有df上进行扩展
depths = pd.concat([depths, expanded_df_bid, expanded_df_ask], axis=1)

depths.index = pd.to_datetime(depths['transact_time'], unit='ms')
depths.index.rename('time', inplace=True);

trades = trades[trades['transact_time'] < depths['transact_time'].iloc[-1]]

먼저 이 20가지 시장 상황의 분포를 살펴보겠습니다. 예상과 일치합니다. 시장 개장 시점이 멀수록 보류 주문이 더 많고 매수 주문과 매도 주문은 대략 대칭적입니다.

bid_mean_list = []
ask_mean_list = []
for i in range(20):
    bid_mean_list.append(round(depths[f'bid_{i}_quantity'].mean(),0))
    ask_mean_list.append(round(depths[f'ask_{i}_quantity'].mean(),0))
plt.figure(figsize=(10, 5))
plt.plot(bid_mean_list);
plt.plot(ask_mean_list);
plt.grid(True)

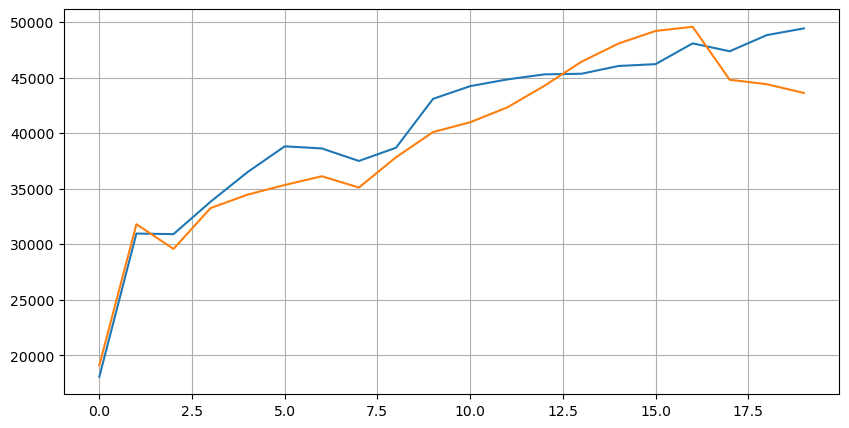
예측 정확도를 평가하기 쉽게 하기 위해 심도 데이터와 거래 데이터를 결합합니다. 여기서 우리는 거래 데이터가 깊이 데이터보다 늦다는 것을 보장합니다. 지연을 고려하지 않고 예측된 값과 실제 거래 가격 사이의 평균 제곱 오차를 직접 계산합니다. 예측의 정확도를 측정하는 데 사용됩니다.

결과를 보면, 매수-매도 쌍의 평균인 mid_price의 오차가 가장 큽니다. weight_mid_price로 변경한 후 오차는 즉시 훨씬 작아지고, 가중 mid-price를 조정하여 더욱 개선됩니다. 어제 기사가 나온 후, 몇몇 사람들은 I^3/2만 사용했다고 보고했습니다. 저는 여기에서 확인했고 결과가 더 좋았습니다. 이유를 생각해보니 사건의 빈도 차이일 것이다. I가 -1과 1에 가까울 때는 확률이 낮은 사건이다. 이런 낮은 확률을 바로잡기 위해 고빈도 사건의 예측은 그렇게 정확하지는 않습니다. 따라서 더 높은 빈도의 이벤트를 처리하기 위해 매개변수를 다시 조정했습니다(이것들은 순수하게 테스트된 매개변수이며 실제 참조 값은 그다지 중요하지 않습니다):

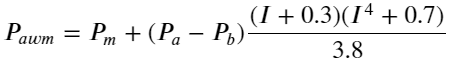
결과는 약간 더 좋았습니다. 이전 기사에서 언급했듯이, 전략은 더 많은 데이터로 예측되어야 합니다. 더 많은 깊이와 주문 이행 데이터로 시장 가격과 얽힘을 통해 얻을 수 있는 개선은 이미 매우 약합니다.

df = pd.merge_asof(trades, depths, on='transact_time', direction='backward')

df['spread'] = round(df['ask_0_price'] - df['bid_0_price'],4)
df['mid_price'] = (df['bid_0_price']+ df['ask_0_price']) / 2
df['I'] = (df['bid_0_quantity'] - df['ask_0_quantity']) / (df['bid_0_quantity'] + df['ask_0_quantity'])
df['weight_mid_price'] = df['mid_price'] + df['spread']*df['I']/2
df['adjust_mid_price'] = df['mid_price'] + df['spread']*(df['I'])*(df['I']**8+1)/4
df['adjust_mid_price_2'] = df['mid_price'] + df['spread']*df['I']*(df['I']**2+1)/4
df['adjust_mid_price_3'] = df['mid_price'] + df['spread']*df['I']**3/2
df['adjust_mid_price_4'] = df['mid_price'] + df['spread']*(df['I']+0.3)*(df['I']**4+0.7)/3.8

print('平均值     mid_price的误差：', ((df['price']-df['mid_price'])**2).sum())
print('挂单量加权 mid_price的误差：', ((df['price']-df['weight_mid_price'])**2).sum())
print('调整后的   mid_price的误差：', ((df['price']-df['adjust_mid_price'])**2).sum())
print('调整后的 mid_price_2的误差：', ((df['price']-df['adjust_mid_price_2'])**2).sum())
print('调整后的 mid_price_3的误差：', ((df['price']-df['adjust_mid_price_3'])**2).sum())
print('调整后的 mid_price_4的误差：', ((df['price']-df['adjust_mid_price_4'])**2).sum())

平均值     mid_price的误差： 0.0048751924999999845
挂单量加权 mid_price的误差： 0.0048373440193987035
调整后的   mid_price的误差： 0.004803654771638586
调整后的 mid_price_2的误差： 0.004808216498329721
调整后的 mid_price_3的误差： 0.004794984755260528
调整后的 mid_price_4的误差： 0.0047909595497071375

두 번째 기어 깊이를 고려하세요

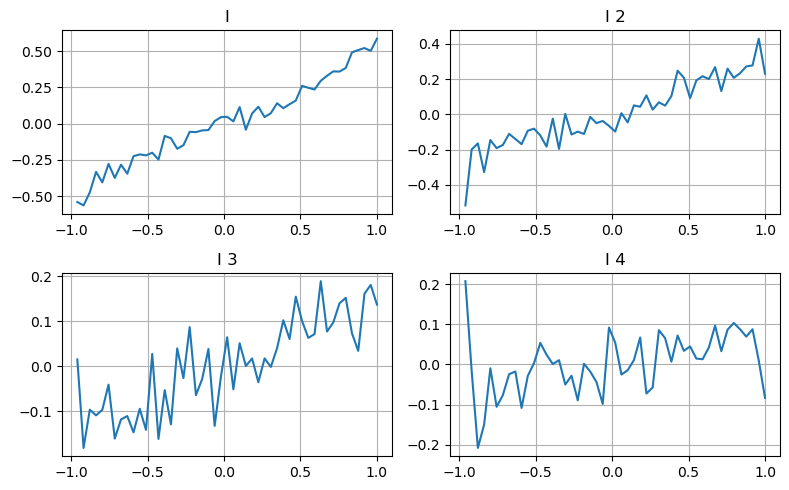
여기서는 이전 기사의 아이디어를 활용해 특정 영향 매개변수의 다양한 값 범위와 거래 가격의 변화를 조사하여 이 매개변수가 중간 가격에 기여하는 정도를 측정합니다. 첫 번째 레벨의 깊이 그래프에서 보듯이 I가 증가함에 따라 다음 거래 가격이 긍정적으로 변경될 가능성이 더 크며, 이는 I가 긍정적인 기여를 한다는 것을 의미합니다.

두 번째 배치도 같은 방식으로 처리하였고, 효과는 첫 번째 배치보다 약간 작았지만 여전히 무시할 수 없는 수준이라는 것을 알 수 있었습니다. 세 번째 단계의 깊이도 약간 기여하지만 단조성이 훨씬 나쁘고 더 깊은 깊이는 기본적으로 참조 가치가 없습니다.

다양한 기여 수준에 따라 세 수준의 불균형 매개변수에 다른 가중치가 할당됩니다. 실제 검사 결과 예측 오류가 다른 계산 방법에 따라 더욱 감소하는 것으로 나타났습니다.

bins = np.linspace(-1, 1, 50)
df['change'] = (df['price'].pct_change().shift(-1))/tick_size
df['I_bins'] = pd.cut(df['I'], bins, labels=bins[1:])
df['I_2'] = (df['bid_1_quantity'] - df['ask_1_quantity']) / (df['bid_1_quantity'] + df['ask_1_quantity'])
df['I_2_bins'] = pd.cut(df['I_2'], bins, labels=bins[1:])
df['I_3'] = (df['bid_2_quantity'] - df['ask_2_quantity']) / (df['bid_2_quantity'] + df['ask_2_quantity'])
df['I_3_bins'] = pd.cut(df['I_3'], bins, labels=bins[1:])
df['I_4'] = (df['bid_3_quantity'] - df['ask_3_quantity']) / (df['bid_3_quantity'] + df['ask_3_quantity'])
df['I_4_bins'] = pd.cut(df['I_4'], bins, labels=bins[1:])
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(8, 5))


axes[0][0].plot(df.groupby('I_bins')['change'].mean())
axes[0][0].set_title('I')
axes[0][0].grid(True)

axes[0][1].plot(df.groupby('I_2_bins')['change'].mean())
axes[0][1].set_title('I 2')
axes[0][1].grid(True)

axes[1][0].plot(df.groupby('I_3_bins')['change'].mean())
axes[1][0].set_title('I 3')
axes[1][0].grid(True)

axes[1][1].plot(df.groupby('I_4_bins')['change'].mean())
axes[1][1].set_title('I 4')
axes[1][1].grid(True)
plt.tight_layout();

df['adjust_mid_price_4'] = df['mid_price'] + df['spread']*(df['I']+0.3)*(df['I']**4+0.7)/3.8
df['adjust_mid_price_5'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.3*df['I_2'])/2
df['adjust_mid_price_6'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.3*df['I_2'])**3/2
df['adjust_mid_price_7'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.3*df['I_2']+0.3)*((0.7*df['I']+0.3*df['I_2'])**4+0.7)/3.8
df['adjust_mid_price_8'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.2*df['I_2']+0.1*df['I_3']+0.3)*((0.7*df['I']+0.3*df['I_2']+0.1*df['I_3'])**4+0.7)/3.8

print('调整后的 mid_price_4的误差：', ((df['price']-df['adjust_mid_price_4'])**2).sum())
print('调整后的 mid_price_5的误差：', ((df['price']-df['adjust_mid_price_5'])**2).sum())
print('调整后的 mid_price_6的误差：', ((df['price']-df['adjust_mid_price_6'])**2).sum())
print('调整后的 mid_price_7的误差：', ((df['price']-df['adjust_mid_price_7'])**2).sum())
print('调整后的 mid_price_8的误差：', ((df['price']-df['adjust_mid_price_8'])**2).sum())

调整后的 mid_price_4的误差： 0.0047909595497071375
调整后的 mid_price_5的误差： 0.0047884350488318714
调整后的 mid_price_6的误差： 0.0047778319053133735
调整后的 mid_price_7的误差： 0.004773578540592192
调整后的 mid_price_8的误差： 0.004771415189297518

거래 데이터를 고려하세요

거래 데이터는 롱 포지션과 숏 포지션의 정도를 직접적으로 반영합니다. 결국, 이것은 실제 돈이 관련된 옵션이고, 주문을 하는 데 드는 비용이 훨씬 낮으며, 고의적인 주문 배치 사기 사례도 있습니다. 따라서 중간 가격을 예측할 때 전략은 거래 데이터에 초점을 맞춰야 합니다.

형태를 고려하여 주문 평균 도착 수량 불균형을 정의합니다. VI, Vb, Vs는 각각 단위 이벤트당 매수 주문 및 매도 주문의 평균 수량을 나타냅니다.

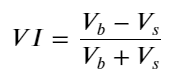
결과는 단기간의 도착량이 가격변화를 예측하는 데 가장 유의미하다는 것을 보여준다. VI가 (0.1-0.9) 사이일 때는 가격과 음의 상관관계를 갖지만, 범위를 벗어나면 가격과 양의 상관관계를 갖는다. 가격. 이는 시장이 극단적이지 않을 때 주로 변동이 특징이며 가격은 평균으로 돌아갈 것임을 시사합니다. 매수 주문이 대량으로 매도 주문을 압도하는 등 극단적인 시장 상황이 발생하면 추세가 추세에서 벗어날 것입니다. . 이러한 낮은 확률 상황을 무시하고 추세와 VI가 음의 선형 관계를 만족한다고 가정하더라도 중간 가격의 예측 오차는 크게 줄어듭니다. 공식의 a는 계수를 나타냅니다.

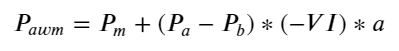
alpha=0.1

df['avg_buy_interval'] = None
df['avg_sell_interval'] = None
df.loc[df['is_buyer_maker'] == True, 'avg_buy_interval'] = df[df['is_buyer_maker'] == True]['transact_time'].diff().ewm(alpha=alpha).mean()
df.loc[df['is_buyer_maker'] == False, 'avg_sell_interval'] = df[df['is_buyer_maker'] == False]['transact_time'].diff().ewm(alpha=alpha).mean()

df['avg_buy_quantity'] = None
df['avg_sell_quantity'] = None
df.loc[df['is_buyer_maker'] == True, 'avg_buy_quantity'] = df[df['is_buyer_maker'] == True]['quantity'].ewm(alpha=alpha).mean()
df.loc[df['is_buyer_maker'] == False, 'avg_sell_quantity'] = df[df['is_buyer_maker'] == False]['quantity'].ewm(alpha=alpha).mean()

df['avg_buy_quantity'] = df['avg_buy_quantity'].fillna(method='ffill')
df['avg_sell_quantity'] = df['avg_sell_quantity'].fillna(method='ffill')
df['avg_buy_interval'] = df['avg_buy_interval'].fillna(method='ffill')
df['avg_sell_interval'] = df['avg_sell_interval'].fillna(method='ffill')

df['avg_buy_rate'] = 1000 / df['avg_buy_interval']
df['avg_sell_rate'] =1000 / df['avg_sell_interval']

df['avg_buy_volume'] = df['avg_buy_rate']*df['avg_buy_quantity']
df['avg_sell_volume'] = df['avg_sell_rate']*df['avg_sell_quantity']

df['I'] = (df['bid_0_quantity']- df['ask_0_quantity']) / (df['bid_0_quantity'] + df['ask_0_quantity'])
df['OI'] = (df['avg_buy_rate']-df['avg_sell_rate']) / (df['avg_buy_rate'] + df['avg_sell_rate'])
df['QI'] = (df['avg_buy_quantity']-df['avg_sell_quantity']) / (df['avg_buy_quantity'] + df['avg_sell_quantity'])
df['VI'] = (df['avg_buy_volume']-df['avg_sell_volume']) / (df['avg_buy_volume'] + df['avg_sell_volume'])

bins = np.linspace(-1, 1, 50)
df['VI_bins'] = pd.cut(df['VI'], bins, labels=bins[1:])
plt.plot(df.groupby('VI_bins')['change'].mean());
plt.grid(True)

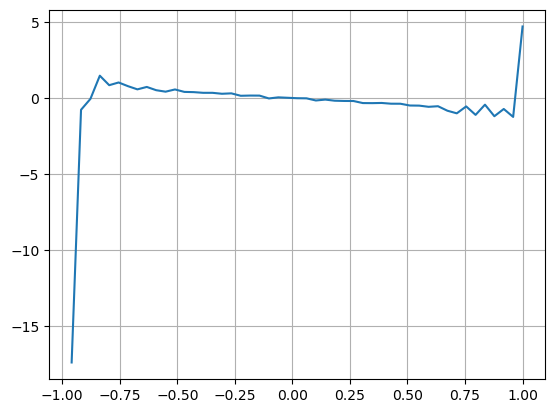
df['adjust_mid_price'] = df['mid_price'] + df['spread']*df['I']/2
df['adjust_mid_price_9'] = df['mid_price'] + df['spread']*(-df['OI'])*2
df['adjust_mid_price_10'] = df['mid_price'] + df['spread']*(-df['VI'])*1.4

print('调整后的mid_price   的误差：', ((df['price']-df['adjust_mid_price'])**2).sum())
print('调整后的mid_price_9 的误差：', ((df['price']-df['adjust_mid_price_9'])**2).sum())
print('调整后的mid_price_10的误差：', ((df['price']-df['adjust_mid_price_10'])**2).sum())

调整后的mid_price   的误差： 0.0048373440193987035
调整后的mid_price_9 的误差： 0.004629586542840461
调整后的mid_price_10的误差： 0.004401790287167206

종합 중간 가격

보류 중인 주문과 거래 데이터가 모두 중간 가격을 예측하는 데 도움이 된다는 점을 고려하면 이 두 매개변수를 결합할 수 있습니다. 여기서 가중치 할당은 임의적이며 경계 조건을 고려하지 않습니다. 극단적인 경우 예측된 중간 가격은 다음과 같을 수 있습니다. 하나를 사고 하나를 파는 것의 차이는 있지만, 오차를 줄일 수만 있다면 이런 세부 사항은 중요하지 않습니다.

마지막으로 예측 오류는 초기 0.00487에서 0.0043으로 떨어졌습니다. 여기서는 자세히 설명하지 않겠습니다. 중간 가격에 대해 알아볼 것이 아직 많이 있습니다. 결국 중간 가격을 예측하는 것은 가격을 예측하는 것입니다. 직접 시도해 볼 수 있습니다. .

#注意VI需要延后一个使用
df['price_change'] = np.log(df['price']/df['price'].rolling(40).mean())
df['CI'] = -1.5*df['VI'].shift()+0.7*(0.7*df['I']+0.2*df['I_2']+0.1*df['I_3'])**3 + 150*df['price_change'].shift(1)

df['adjust_mid_price_11'] = df['mid_price'] + df['spread']*(df['CI'])
print('调整后的mid_price_11的误差：', ((df['price']-df['adjust_mid_price_11'])**2).sum())

调整后的mid_price_11的误差： 0.00421125960463469

요약하다

이 논문은 심도 데이터와 거래 데이터를 결합하여 중간 가격의 계산 방법을 더욱 개선합니다. 이 논문은 정확도를 측정하는 방법을 제공하고 가격 변화를 예측하는 정확도를 개선합니다. 전반적으로 다양한 매개변수는 그다지 엄격하지 않으며 단지 참고용일 뿐입니다. 더 정확한 중간 가격을 가지고, 다음 단계는 백테스팅을 위해 실제로 중간 가격을 적용하는 것입니다. 이 부분도 내용이 많으므로, 잠시 업데이트를 중단할 것입니다.