이 글에서는 데이 트레이딩 전략을 알아보겠습니다. 이는 “평균 회귀 거래 쌍”의 고전적 거래 개념을 사용합니다. 이 예에서 우리는 뉴욕 증권 거래소(NYSE)에서 거래되는 두 개의 상장지수펀드(ETF)인 SPY와 IWM을 활용하여 미국 주식 시장 지수인 S&P 500과 Russell 2000을 표현해 보려고 합니다. .

이 전략은 한 ETF를 롱 포지션으로, 다른 ETF를 숏 포지션으로 잡는 “캐리” 전략을 만들어냅니다. 롱-숏 비율은 다양한 방법으로 정의할 수 있는데, 예를 들어 통계적 공적분 시계열 방법을 사용할 수 있습니다. 이 시나리오에서는 롤링 선형 회귀를 통해 SPY와 IWM 간의 헤지 비율을 계산합니다. 이를 통해 SPY와 IWM 사이의 “스프레드”를 생성할 수 있으며, 이는 z-점수로 정규화됩니다. z-점수가 특정 임계값을 초과하면 이 “스프레드”가 평균으로 회귀할 것이라고 믿기 때문에 거래 신호가 생성됩니다.

이러한 전략의 근거는 SPY와 IWM이 둘 다 거의 동일한 시장 시나리오, 즉 대형 및 소규모 미국 기업의 주가 실적을 나타낸다는 것입니다. 전제는 만약 당신이 가격의 “평균 회귀” 이론을 받아들인다면 그것은 항상 회귀할 것이라는 것입니다. 왜냐하면 “사건”이 매우 짧은 기간 내에 S&P500과 Russell 2000에 개별적으로 영향을 미칠 수 있지만, 두 이론 사이의 “이자율 차이”는 그들은 항상 정상적인 평균으로 회귀할 것이고, 둘의 장기 가격 시리즈는 항상 공적분됩니다.

전략

전략은 다음과 같이 실행됩니다.

데이터 - 2007년 4월부터 2014년 2월까지의 SPY와 IWM의 1분 캔들스틱 차트를 받아보세요.

처리 - 데이터를 올바르게 정렬하고 서로 누락된 막대를 삭제합니다. (한쪽 면이 누락된 경우, 양쪽 모두 삭제됩니다)

스프레드 - 두 ETF 간의 헤지 비율은 롤링 선형 회귀 분석을 사용하여 계산됩니다. 룩백 윈도우를 1바 앞으로 이동하고 회귀 계수를 다시 계산하여 베타 회귀 계수로 정의합니다. 따라서 헤지 비율 βi, bi K-line은 bi-1-k에서 bi-1로의 교차점을 계산하여 K-라인을 추적하는 데 사용됩니다.

Z-점수 - 표준 스프레드의 값은 일반적인 방식으로 계산됩니다. 즉, 표본의 평균을 빼고 표준편차로 나누는 것을 의미합니다. 이렇게 하는 이유는 Z-점수가 무차원 양이기 때문에 임계값 매개변수를 이해하기 쉽게 만들기 위해서입니다. 저는 의도적으로 “미래 예측 편향”을 계산에 도입하여 그것이 얼마나 미묘할 수 있는지 보여드리고자 했습니다. 한번 시도해 보세요!

트레이딩 - 롱 신호는 음의 z-점수 값이 사전 결정된(또는 최적화된) 임계값 아래로 떨어지면 생성되고, 숏 신호는 그 반대의 경우 생성됩니다. z-점수의 절대값이 추가 임계값 아래로 떨어지면 포지션을 종료하라는 신호가 생성됩니다. 이 전략의 경우, 저는 (다소 임의적으로) 진입 임계값으로 |z| = 2를, 종료 임계값으로 |z| = 1을 선택했습니다. 평균 회귀가 스프레드에 영향을 미친다고 가정하면, 위의 내용이 이러한 차익 거래 관계를 포착하여 괜찮은 수익을 제공할 수 있을 것으로 기대됩니다.

아마도 전략을 깊이 이해하는 가장 좋은 방법은 실제로 전략을 실행하는 것입니다. 다음 섹션에서는 이 평균 회귀 전략을 구현하는 데 사용된 전체 Python 코드(단일 파일)를 자세히 설명합니다. 더 잘 이해하실 수 있도록 자세한 코드 주석을 추가했습니다.

파이썬 구현

모든 Python/pandas 튜토리얼과 마찬가지로, 이 튜토리얼에서 설명한 대로 Python 환경을 설정해야 합니다. 설정이 완료되면 첫 번째 작업은 필요한 Python 라이브러리를 가져오는 것입니다. 이는 matplotlib과 pandas를 사용하는 데 필요합니다.

내가 사용하고 있는 구체적인 라이브러리 버전은 다음과 같습니다.

Python - 2.7.3 NumPy - 1.8.0 pandas - 0.12.0 matplotlib - 1.1.0

이제 다음 라이브러리를 가져와 보겠습니다.

# mr_spy_iwm.py

import matplotlib.pyplot as plt
import numpy as np
import os, os.path
import pandas as pd

다음 함수 create_pairs_dataframe은 두 가지 심볼의 일중 캔들스틱을 포함하는 두 개의 CSV 파일을 가져옵니다. 우리의 경우에는 SPY와 IWM이 될 것입니다. 그런 다음 두 원본 파일의 인덱스를 사용하는 별도의 “데이터 프레임 쌍”을 생성합니다. 누락된 거래 및 오류로 인해 타임스탬프가 달라질 수 있습니다. 이는 판다스와 같은 데이터 분석 라이브러리를 사용하는 주요 이점 중 하나입니다. 우리는 매우 효율적인 방식으로 “보일러플레이트” 코드를 처리합니다.

# mr_spy_iwm.py
def create_pairs_dataframe(datadir, symbols):
    """Creates a pandas DataFrame containing the closing price
    of a pair of symbols based on CSV files containing a datetime
    stamp and OHLCV data."""
 
    # Open the individual CSV files and read into pandas DataFrames
    print "Importing CSV data..."
    sym1 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[0]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
    sym2 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[1]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
 
    # Create a pandas DataFrame with the close prices of each symbol
    # correctly aligned and dropping missing entries
    print "Constructing dual matrix for %s and %s..." % symbols    
    pairs = pd.DataFrame(index=sym1.index)
    pairs['%s_close' % symbols[0].lower()] = sym1['close']
    pairs['%s_close' % symbols[1].lower()] = sym2['close']
    pairs = pairs.dropna()
    return pairs

다음 단계는 SPY와 IWM 사이에서 롤링 선형 회귀 분석을 하는 것입니다. 이 시나리오에서 IWM은 예측 변수(‘x’)이고 SPY는 응답 변수(‘y’)입니다. 저는 기본 룩백 윈도우를 100개 캔들스틱으로 설정했습니다. 앞서 언급한 것처럼 이것이 전략의 매개변수입니다. 전략이 견고한 것으로 간주되려면 이상적으로는 추적 기간(또는 다른 성과 측정)에 걸쳐 볼록한 수익 보고서를 보고 싶습니다. 따라서 코드의 이후 단계에서는 범위 내에서 검토 기간을 변경하여 민감도 분석을 수행하게 됩니다.

SPY-IWM의 선형 회귀 모델에서 롤링 베타 계수를 계산한 후 이를 DataFrame 쌍에 추가하고 빈 행을 제거합니다. 이는 룩백 길이의 트리밍된 측정값과 동일한 첫 번째 촛대 세트를 구성합니다. 그런 다음 SPY 1단위와 IWM -βi 1단위로 두 ETF 간의 스프레드를 생성했습니다. 분명히 이는 현실적인 시나리오가 아닙니다. 실제 구현에서는 불가능한 소량의 IWM을 사용하고 있기 때문입니다.

마지막으로, 산포의 평균을 빼고 산포의 표준편차로 정규화하여 산포의 z-점수를 계산합니다. 여기에는 다소 미묘한 “미래 지향적 편견”이 작용하고 있다는 점을 알아두는 것이 중요합니다. 연구에서 이런 실수를 하기 쉽다는 것을 강조하고 싶어서 의도적으로 코드에 그대로 두었습니다. 전체 확산 시계열의 평균과 표준 편차를 계산합니다. 이것이 진정한 역사적 정확성을 반영하려는 것이라면, 이 정보는 암묵적으로 미래의 정보를 활용하기 때문에 얻을 수 없습니다. 그러므로 z-점수를 계산하려면 이동 평균과 표준 편차를 사용해야 합니다.

# mr_spy_iwm.py
 
def calculate_spread_zscore(pairs, symbols, lookback=100):
    """Creates a hedge ratio between the two symbols by calculating
    a rolling linear regression with a defined lookback period. This
    is then used to create a z-score of the 'spread' between the two
    symbols based on a linear combination of the two."""
     
    # Use the pandas Ordinary Least Squares method to fit a rolling
    # linear regression between the two closing price time series
    print "Fitting the rolling Linear Regression..."
    model = pd.ols(y=pairs['%s_close' % symbols[0].lower()], 
                   x=pairs['%s_close' % symbols[1].lower()],
                   window=lookback)
 
    # Construct the hedge ratio and eliminate the first 
    # lookback-length empty/NaN period
    pairs['hedge_ratio'] = model.beta['x']
    pairs = pairs.dropna()
 
    # Create the spread and then a z-score of the spread
    print "Creating the spread/zscore columns..."
    pairs['spread'] = pairs['spy_close'] - pairs['hedge_ratio']*pairs['iwm_close']
    pairs['zscore'] = (pairs['spread'] - np.mean(pairs['spread']))/np.std(pairs['spread'])
    return pairs

create_long_short_market_signals에서 거래 신호를 생성합니다. 이는 임계값을 초과하는 z-점수 값을 측정하여 계산됩니다. z-점수의 절대값이 다른 (더 작은) 임계값보다 작거나 같으면 포지션을 종료하라는 신호가 주어집니다.

이를 달성하려면 각 K-라인에 대한 거래 전략이 ‘오픈’인지 ‘클로징’인지 확립해야 합니다. Long_market과 short_market은 롱 포지션과 숏 포지션을 추적하기 위해 정의된 두 가지 변수입니다. 불행히도, 벡터화된 접근 방식보다 반복적인 방식으로 프로그래밍하는 것이 훨씬 간단하기 때문에 계산 속도가 느립니다. 1분 캔들스틱 차트에는 CSV 파일당 약 70만 개의 데이터 포인트가 필요하지만, 오래된 데스크톱에서도 비교적 빠르게 계산할 수 있어요!

pandas DataFrame을 반복하려면(인정하건대 흔하지 않은 작업) 반복 가능한 생성기를 제공하는 iterrows 메서드를 사용해야 합니다.

# mr_spy_iwm.py
 
def create_long_short_market_signals(pairs, symbols, 
                                     z_entry_threshold=2.0, 
                                     z_exit_threshold=1.0):
    """Create the entry/exit signals based on the exceeding of 
    z_enter_threshold for entering a position and falling below
    z_exit_threshold for exiting a position."""
 
    # Calculate when to be long, short and when to exit
    pairs['longs'] = (pairs['zscore'] <= -z_entry_threshold)*1.0
    pairs['shorts'] = (pairs['zscore'] >= z_entry_threshold)*1.0
    pairs['exits'] = (np.abs(pairs['zscore']) <= z_exit_threshold)*1.0
 
    # These signals are needed because we need to propagate a
    # position forward, i.e. we need to stay long if the zscore
    # threshold is less than z_entry_threshold by still greater
    # than z_exit_threshold, and vice versa for shorts.
    pairs['long_market'] = 0.0
    pairs['short_market'] = 0.0
 
    # These variables track whether to be long or short while
    # iterating through the bars
    long_market = 0
    short_market = 0
 
    # Calculates when to actually be "in" the market, i.e. to have a
    # long or short position, as well as when not to be.
    # Since this is using iterrows to loop over a dataframe, it will
    # be significantly less efficient than a vectorised operation,
    # i.e. slow!
    print "Calculating when to be in the market (long and short)..."
    for i, b in enumerate(pairs.iterrows()):
        # Calculate longs
        if b[1]['longs'] == 1.0:
            long_market = 1            
        # Calculate shorts
        if b[1]['shorts'] == 1.0:
            short_market = 1
        # Calculate exists
        if b[1]['exits'] == 1.0:
            long_market = 0
            short_market = 0
        # This directly assigns a 1 or 0 to the long_market/short_market
        # columns, such that the strategy knows when to actually stay in!
        pairs.ix[i]['long_market'] = long_market
        pairs.ix[i]['short_market'] = short_market
    return pairs

이 단계에서는 실제 롱 및 숏 신호를 포함하도록 페어를 업데이트하여 포지션을 열어야 할지 여부를 결정합니다. 이제 우리는 포지션의 시장 가치를 추적하는 포트폴리오를 만들어야 합니다. 첫 번째 작업은 롱 신호와 숏 신호를 결합한 포지션 컬럼을 만드는 것입니다. 여기에는 (1,0,-1)까지의 요소 목록이 포함됩니다. 여기서 1은 롱 포지션을 나타내고, 0은 포지션 없음(닫혀야 함), -1은 숏 포지션을 나타냅니다. sym1과 sym2 열은 각 캔들스틱 끝에서 SPY와 IWM 포지션의 시장 가치를 나타냅니다.

ETF 시장 가치가 생성되면 이를 합산하여 각 캔들스틱의 끝에서 전체 시장 가치를 산출합니다. 그런 다음 해당 객체의 pct_change 메서드를 통해 반환 값으로 변환됩니다. 이후의 코드 줄에서는 오류가 있는 항목(NaN 및 inf 요소)을 정리하고 마지막으로 전체 자본 곡선을 계산합니다.

# mr_spy_iwm.py
 
def create_portfolio_returns(pairs, symbols):
    """Creates a portfolio pandas DataFrame which keeps track of
    the account equity and ultimately generates an equity curve.
    This can be used to generate drawdown and risk/reward ratios."""
     
    # Convenience variables for symbols
    sym1 = symbols[0].lower()
    sym2 = symbols[1].lower()
 
    # Construct the portfolio object with positions information
    # Note that minuses to keep track of shorts!
    print "Constructing a portfolio..."
    portfolio = pd.DataFrame(index=pairs.index)
    portfolio['positions'] = pairs['long_market'] - pairs['short_market']
    portfolio[sym1] = -1.0 * pairs['%s_close' % sym1] * portfolio['positions']
    portfolio[sym2] = pairs['%s_close' % sym2] * portfolio['positions']
    portfolio['total'] = portfolio[sym1] + portfolio[sym2]
 
    # Construct a percentage returns stream and eliminate all 
    # of the NaN and -inf/+inf cells
    print "Constructing the equity curve..."
    portfolio['returns'] = portfolio['total'].pct_change()
    portfolio['returns'].fillna(0.0, inplace=True)
    portfolio['returns'].replace([np.inf, -np.inf], 0.0, inplace=True)
    portfolio['returns'].replace(-1.0, 0.0, inplace=True)
 
    # Calculate the full equity curve
    portfolio['returns'] = (portfolio['returns'] + 1.0).cumprod()
    return portfolio

주요 기능은 모든 것을 하나로 묶습니다. 일중 CSV 파일은 datadir 경로에 있습니다. 다음 코드를 특정 디렉토리를 가리키도록 수정하세요.

전략이 룩백 기간에 얼마나 민감한지 확인하려면 다양한 룩백 성과 지표를 계산해야 합니다. 저는 포트폴리오의 최종 총 수익률 백분율을 성과 지표로 선택했고, 회고 범위도 선택했습니다.[50,200] 10씩 증가합니다. 아래 코드에서 이전 함수가 이 범위에 대해 for 루프로 래핑되었고 다른 임계값은 동일하게 유지되는 것을 볼 수 있습니다. 마지막 작업은 matplotlib을 사용하여 룩백 대비 수익의 선형 차트를 만드는 것입니다.

# mr_spy_iwm.py
 
if __name__ == "__main__":
    datadir = '/your/path/to/data/'  # Change this to reflect your data path!
    symbols = ('SPY', 'IWM')
 
    lookbacks = range(50, 210, 10)
    returns = []
 
    # Adjust lookback period from 50 to 200 in increments
    # of 10 in order to produce sensitivities
    for lb in lookbacks: 
        print "Calculating lookback=%s..." % lb
        pairs = create_pairs_dataframe(datadir, symbols)
        pairs = calculate_spread_zscore(pairs, symbols, lookback=lb)
        pairs = create_long_short_market_signals(pairs, symbols, 
                                                z_entry_threshold=2.0, 
                                                z_exit_threshold=1.0)
 
        portfolio = create_portfolio_returns(pairs, symbols)
        returns.append(portfolio.ix[-1]['returns'])
 
    print "Plot the lookback-performance scatterchart..."
    plt.plot(lookbacks, returns, '-o')
    plt.show()

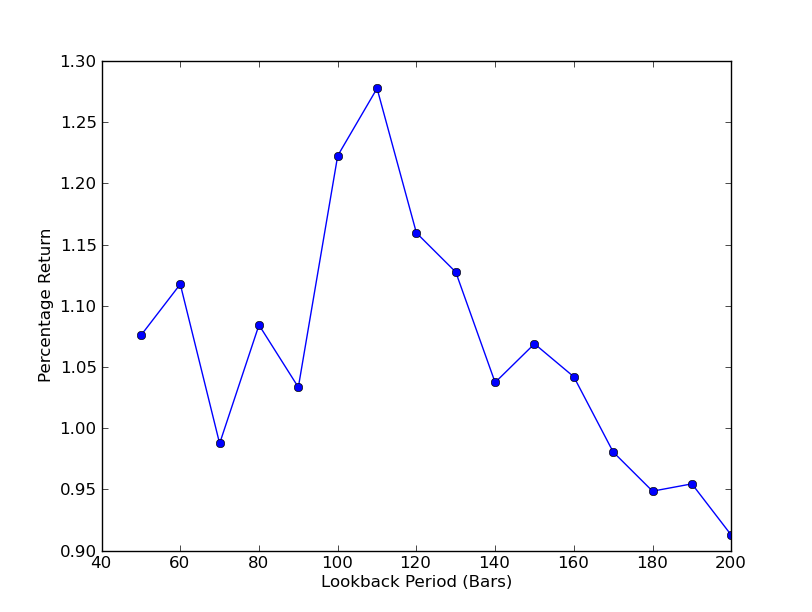
이제 룩백과 수익의 그래프를 볼 수 있습니다. 룩백의 경우 “전역” 최대값이 110개 막대라는 점에 유의하세요. 룩백이 수익과 아무런 관련이 없는 상황이 있는 경우, 그 이유는 다음과 같습니다.

SPY-IWM 선형 회귀 헤지 비율 룩백 기간 민감도 분석

상승하는 수익 곡선이 없다면 백테스팅 기사는 완성되지 않습니다! 따라서 시간에 따른 누적 이익수익률을 표시하려면 다음 코드를 사용하면 됩니다. 이는 회고 매개변수 연구로부터 생성된 최종 포트폴리오를 표시합니다. 따라서 시각화하려는 차트에 맞게 룩백을 선택하는 것이 필요합니다. 이 차트는 비교를 돕기 위해 동일 기간 동안의 SPY 수익률도 표시합니다.

# mr_spy_iwm.py
 
    # This is still within the main function
    print "Plotting the performance charts..."
    fig = plt.figure()
    fig.patch.set_facecolor('white')
 
    ax1 = fig.add_subplot(211,  ylabel='%s growth (%%)' % symbols[0])
    (pairs['%s_close' % symbols[0].lower()].pct_change()+1.0).cumprod().plot(ax=ax1, color='r', lw=2.)
 
    ax2 = fig.add_subplot(212, ylabel='Portfolio value growth (%%)')
    portfolio['returns'].plot(ax=ax2, lw=2.)
 
    fig.show()

아래의 주식 곡선 차트는 100일의 회고 기간을 갖습니다.

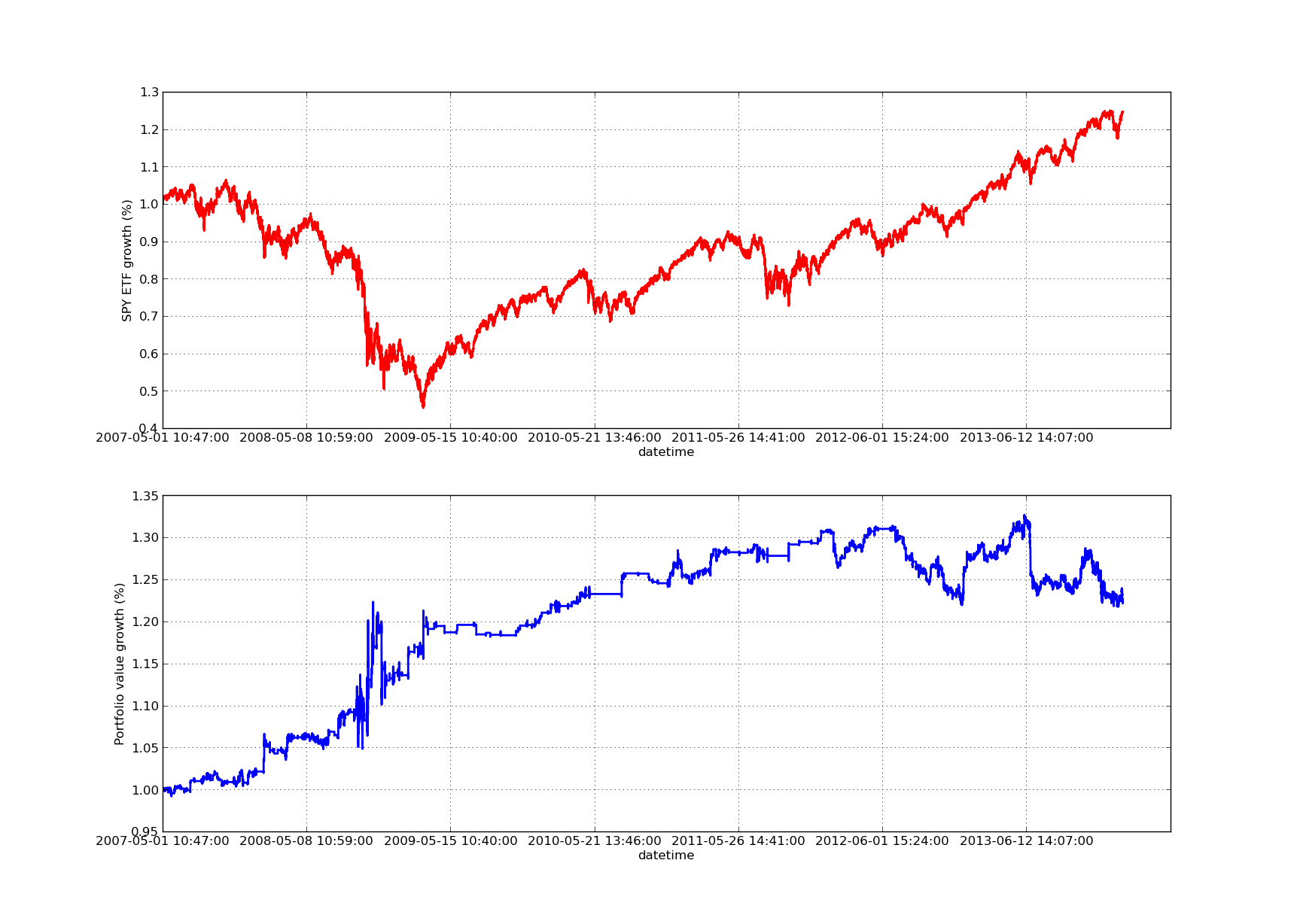
SPY-IWM 선형 회귀 헤지 비율 룩백 기간 민감도 분석

2009년 금융 위기 때 SPY 인출액이 상당히 컸다는 점에 유의하세요. 이 단계에서는 전략도 격동의 시기를 겪습니다. 또한, 이 기간 동안 SPY가 S&P 500과 유사한 강력한 추세를 보였기 때문에 지난해 성과가 저하되었다는 점에 유의하세요.

z-점수 분포를 계산할 때 여전히 “미리보기 편향”을 고려해야 한다는 점에 유의하세요. 더욱이 이러한 모든 계산은 거래 비용 없이 수행됩니다. 이러한 요소를 고려하면 이 전략은 효과가 좋지 않을 가능성이 큽니다. 수수료와 슬리피지는 현재로선 결정되지 않았습니다. 또한 이 전략은 ETF의 일부 단위로 거래되는데, 이 역시 매우 비현실적입니다.

향후 기사에서는 위에 나열된 모든 사항을 고려하여 주식 곡선과 성과 지표에 대한 신뢰도를 높이는 보다 복잡한 이벤트 기반 백테스터를 만들 예정입니다.