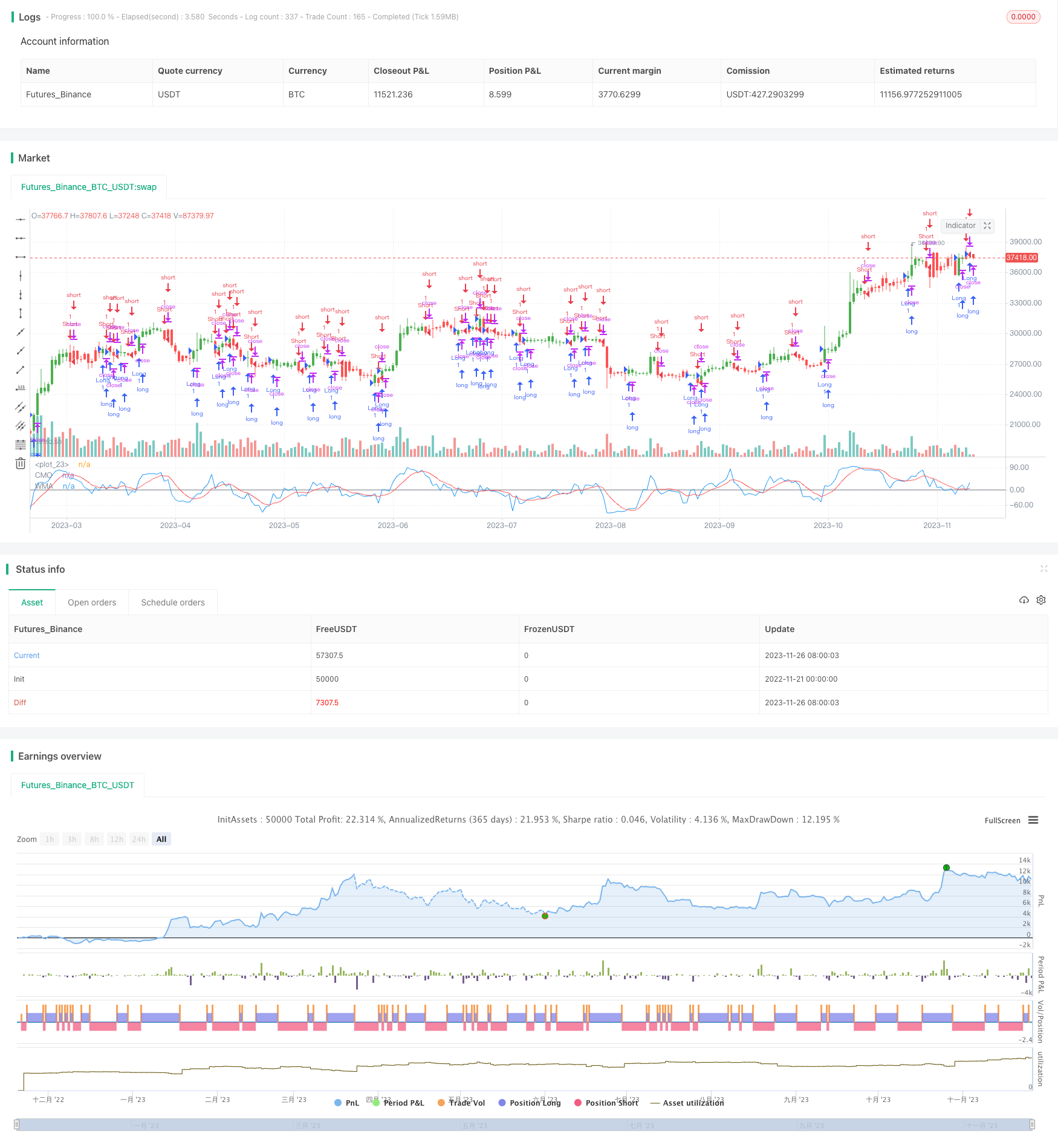
개요
이 전략은 CMO와 WMA에 기반한 동적 거래 전략이라고 불린다. 이 전략은 Chande Momentum Oscillator (CMO) 와 그 중화 이동 평균 (WMA) 을 사용하여 거래 신호를 구축한다. 핵심 아이디어는 CMO가 WMA를 밟을 때 더 많이하고 WMA를 밟을 때 더 적게하는 것이다. 동시에 역 거래 옵션을 고려한다.
전략 원칙
이 전략의 핵심 지표는 CMO이다. CMO는 RSI와 같은 다른 동적 지표와 밀접한 관련이 있지만 독특한 특징도 있다. CMO는 가격 변화의 모멘텀을 직접 측정한다.
이 전략은 먼저 1일간의 close 가격의 변화를 계산합니다.[1]) xMom의 원초적인 모멘텀으로 . 그리고 xMom의 스마 (Length day SMA) 를 xSMA_mom로 기록 . 그리고 스마 (Length day price change) 의 스마 (Length day price change) 를 xMomLength로 계산, 즉 close - close[Length]。 최종 CMO 값은 xMomLength를 xSMA_mom에 나누고 100으로 곱한다。 이 CMO는 WMA ((변수 LengthWMA) 에 의해 평평한 후 CMO xWMACMO。 전략 신호는: CMO가 위를 뚫고 (아래를 뚫고) 자신의 WMA를 뚫을 때 더 많이 (공백) 하라。
전략적 이점
이 전략의 가장 큰 장점은 가격 추세에서 동력의 특징을 포착하는 것이다. CMO의 경계 디자인은 동력의 변화를 더 직접적으로 반영하게 한다. SMA, WMA에 비해 단기간의 소음을 더 부드럽게 한다. 따라서 이 전략은 중장선 추세에서 입구점을 효과적으로 식별할 수 있다. 또한 단일 지표에 비해 CMO와 WMA를 조합하여 사용하는 것이 안정성을 향상시킬 수 있다.
전략적 위험
이 전략의 가장 큰 위험은 빈번한 거래로 인한 슬라이드 비용이다. CMO와 WMA는 단기적인 변수이며, 너무 민감하여 여러 번 무의미한 반전을 일으킬 수 있다. 이것은 품종이 큰 변동이 있을 때 특히 심각하다. 또한, 고정된 변수는 시장 환경의 변화에 적응할 수 없다.
자기 적응 변수 최적화 CMO와 WMA의 변수를 도입하여 동적으로 조정할 수 있도록 고려할 수 있습니다. 또는 필터링 조건을 추가하여 무의미한 거래를 줄일 수 있습니다. 물론 조합을 통해 품종 변동성을 줄이는 것도 옵션입니다.
전략 최적화 방향
이 전략은 다음과 같은 부분에서 최적화될 수 있습니다.
다양한 변동 환경 속에서 최적의 매개 변수를 찾는 CMO 매개 변수 메커니즘을 추가합니다.
WMA 매개 변수 메커니즘을 추가한다. 평형 효과는 변동성에 따라 변한다.
필터링 조건을 추가하여, 예를 들어, 변동성 지수를 도입하여, 통제를 역전시킬 수 있습니다.
다른 지표들과의 조합을 고려하여 안정성을 높이는 것;
손해 막기 제도를 최적화한다. 동적 손해 막선을 설정하고, 원륜 손실을 적극적으로 제어한다.
요약하다
이 전략은 CMO와 WMA를 기반으로 간단하고 효과적인 트렌드 추적을 구현한다. 이 전략의 장점은 가격 운동 특성을 명확하게 포착하는 것이다. 그러나 약간의 수익 후 포지션 보유 능력의 단점도 있다. 매개 변수 최적화 및 조합을 통해 안정성을 향상시킬 수 있다.
/*backtest
start: 2022-11-21 00:00:00
end: 2023-11-27 00:00:00
period: 1d
basePeriod: 1h
exchanges: [{"eid":"Futures_Binance","currency":"BTC_USDT"}]
*/
//@version=2
////////////////////////////////////////////////////////////
// Copyright by HPotter v1.0 13/02/2017
// This indicator plots Chandre Momentum Oscillator and its WMA on the
// same chart. This indicator plots the absolute value of CMO.
// The CMO is closely related to, yet unique from, other momentum oriented
// indicators such as Relative Strength Index, Stochastic, Rate-of-Change,
// etc. It is most closely related to Welles Wilder?s RSI, yet it differs
// in several ways:
// - It uses data for both up days and down days in the numerator, thereby
// directly measuring momentum;
// - The calculations are applied on unsmoothed data. Therefore, short-term
// extreme movements in price are not hidden. Once calculated, smoothing
// can be applied to the CMO, if desired;
// - The scale is bounded between +100 and -100, thereby allowing you to clearly
// see changes in net momentum using the 0 level. The bounded scale also allows
// you to conveniently compare values across different securities.
////////////////////////////////////////////////////////////
strategy(title="CMO & WMA", shorttitle="CMO & WMA")
Length = input(9, minval=1)
LengthWMA = input(9, minval=1)
reverse = input(false, title="Trade reverse")
hline(0, color=gray, linestyle=line)
xMom = abs(close - close[1])
xSMA_mom = sma(xMom, Length)
xMomLength = close - close[Length]
nRes = 100 * (xMomLength / (xSMA_mom * Length))
xWMACMO = wma(nRes, LengthWMA)
pos = iff(nRes > xWMACMO, 1,
iff(nRes <= xWMACMO, -1, nz(pos[1], 0)))
possig = iff(reverse and pos == 1, -1,
iff(reverse and pos == -1, 1, pos))
if (possig == 1)
strategy.entry("Long", strategy.long)
if (possig == -1)
strategy.entry("Short", strategy.short)
barcolor(possig == -1 ? red: possig == 1 ? green : blue)
plot(nRes, color=blue, title="CMO")
plot(xWMACMO, color=red, title="WMA")