동적 이중 지수 평활화 이동 평균 거래 전략

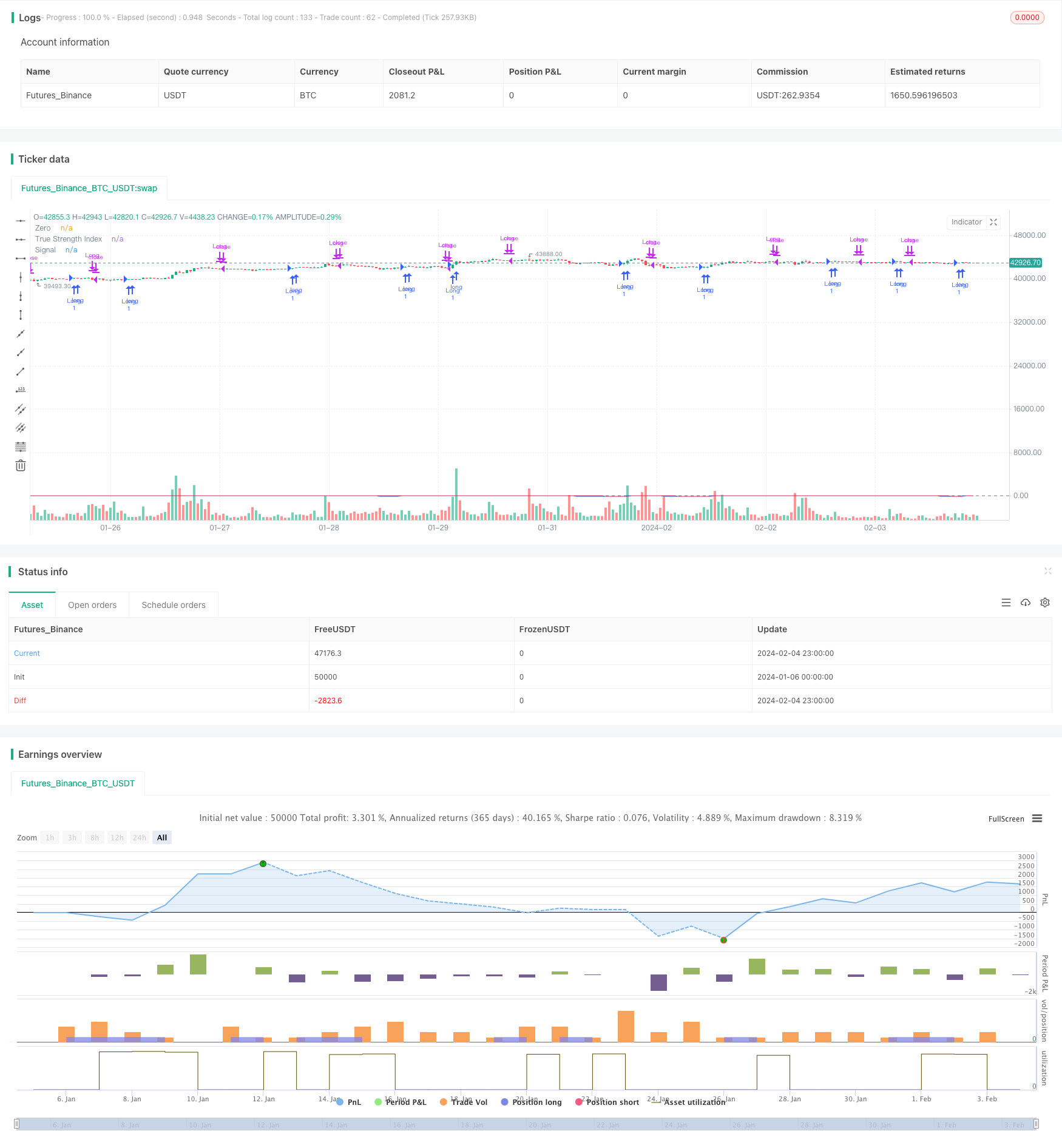
개요

이 전략은 다이내믹 듀얼 지수 평평선 트레이딩 전략으로, 듀얼 지수 평평선 (Double Exponential Moving Average, DEMA) 에 기반한 정량적 트레이딩 전략이다. 이 전략은 주식의 가격 변화율을 계산한 다음, 그 절대값과 비-절대값을 각각 듀얼 지수 평평 처리하여 실제 강도 지수 (True Strength Index, TSI) 를 얻는다.

전략 원칙

이 전략의 핵심 지표는 실제 강도 지수 (TSI) 이다.TSI의 계산 공식은 다음과 같다.

TSI = 100 * (PC1 / PC2)

그 중 PC1과 PC2는 각각 가격 변화율의 이중 지수 평평선과 가격 변화율의 절대값의 이중 지수 평평선이다. 이중 지수 평평선의 계산 과정은 우선 가격 변화율에 한 기간의 지수 이동 평균을 적용한 다음, 그 다음으로 얻은 지수 이동 평균에 또 다른 짧은 기간의 지수 이동 평균을 적용한 것이다. 이렇게 이중 평평화를 통해 가격 변화율의 무작위성을 더 잘 제거할 수 있으며, 이로 인해 TSI 지수의 안정성을 높인다.

TSI 값을 계산한 후, 전략은 TSI 값의 신호선을 계산합니다. 신호선은 TSI 값의 일정한 기간의 지수 이동 평균으로 정의됩니다. 실제 거래 시, 전략은 TSI 값과 신호선과의 관계를 관찰하여 시장 추세를 판단하고 거래 신호를 생성합니다.

이 전략의 또 다른 특징은 거래 크기가 동적으로 조정된다는 것입니다. 전략 코드에는 초기 자본과 리스크 포지션 비율이 입력 파라미트로 설정되어 있습니다. 이 두 가지 파라미트는 주식의 당시 가격과 결합하여 매번의 거래 수 또는 리스크 포지션을 동적으로 계산합니다.

우위 분석

동적 쌍 지수 이동 평균 거래 전략은 다양한 장점을 제공합니다:

1. 이 지표는 두 개의 지수 평준화를 적용하여 시장 소음에 대한 감수성을 감소시키고 더 정확한 신호를 생성 할 수 있습니다.

2. 이것은 거래 신호를 생성하기 위해 지표와 신호선을 교차하는 검증 된 원칙에 기초합니다. 이것은 많은 가짜 신호를 제거합니다.

3. 이 전략은 리스크 예산 동성에 따라 포지션 크기를 조정한다. 이것은 과도한 거래와 감정적 인 조작을 방지하는 데 도움이됩니다.

4. 그것은 매일 및 주간 시간 프레임에 적용되며, 스윙 거래와 위치 거래에 적합하다.

5. 간단한 입출력 논리 때문에 로봇과 다른 거래 시스템에서 쉽게 구현된다.

6. 너무 많은 변수가 필요없고, 최적화 시스템을 간단하게 만들 수 있습니다.

이러한 장점들이 함께 그것을 주식 거래자의 강력하고 다능한 거래 전략으로 만든다. 신중한 부드러운 처리와 위치 크기의 설정은 가짜 신호와 큰 손실을 방지하는 데 도움이됩니다.

위험 분석

동적 쌍 지수 이동 평균 거래 전략은 장점이 많지만, 대부분의 주식 전략과 마찬가지로 몇 가지 고유한 위험이 있습니다.

1. TSI와 신호선은 역사적 가격 데이터에 기반하기 때문에, 특히 시장의 변동성이 강한 상황에서, 잘못된 신호의 위험이 항상 존재한다.

2. 시장이 TSI 지표의 0선 주변에 흔들리면 회전이 발생할 수 있습니다. 이것은 손실을 초래할 수 있습니다.

3. 큰 폭의 하락… 트렌드가 지속된다면, TSI는 조기 하락하여 수익을 놓칠 수 있다.

4. 리버리지의 영향으로, 리스크 파라미터가 설정한 한계보다 더 큰 손실이 발생할 수 있습니다.

그러나, 포지션 크기, 정지 및 기타 위험 관리 기술과 같은 측면을 적용함으로써 이러한 위험을 완화 할 수 있습니다. 또한, 변수 및 필터는 다양한 시장 조건에서 성능을 극대화하기 위해 추가로 최적화 할 수 있습니다.

최적화 방향

이 전략의 최적화를 위한 몇 가지 아이디어는 다음과 같습니다.

1. 더 정확한 거래 신호를 생성할 수 있는 조합을 찾기 위해 다양한 이중 평준화 파라미터 조합을 테스트하십시오. 긴 짧은 주기 파라미터를 조정하여 최적화 할 수 있습니다.

2. 변동률, 거래량 또는 다른 지표에 기반한 필터를 추가하여 불필요한 거래 신호를 줄일 수 있습니다. 이는 거래 주파수를 줄일 수 있으며 거래당 수익성을 높일 수 있습니다.

3. 스톱 로직을 추가한다. 예를 들어, TSI 값이 0축을 통과할 때 스톱한다. 이것은 불필요한 손실을 줄일 수 있다.

4. 이 전략에 따라 지수, 상품 등과 같은 다양한 거래 품종의 성과를 평가하십시오. 가장 잘하는 품종을 선택하십시오.

5. 거래 품종에 대한 선택적 필터링. 예를 들어, 품종의 유동성, 변동률 지표를 평가하고, 매개 변수 지표 순위가 높은 품종을 선택하여 거래한다.

6. 기계학습을 이용한 방법 앞으로 분석하는 방법 최적의 파라미터 조합을 선택한다. 이것은 인공 선택으로 인한 편견을 줄이고 더 우수한 파라미터들을 얻을 수 있다.

7. 다양한 시장 환경에 따라 여러 개의 파라미트 세트를 사용하며 동적으로 전환한다. 예를 들어, 황소 시장에서는 더 적극적인 파라미트 세트를 사용할 수 있으며, 곰 시장에서는 더 보수적인 조합을 사용합니다.

이 전략의 안정성과 수익률을 테스트하고 최적화함으로써 더욱 향상시킬 수 있을 것입니다.

요약하다

종합적으로 이 전략은 TSI 지표의 이중 지수 평평성을 기반으로 비교적 안정적이고 신뢰할 수 있는 주식 거래 전략을 설계했다. 포지션 규모를 동적으로 조정함으로써 전체의 위험 수준을 효과적으로 제어할 수 있다. 이 전략은 단선 및 중장선 거래에 적합한 장점을 동시에 갖는다.

물론, 대부분의 양적 거래 전략과 마찬가지로, 이 전략에도 한계가 있습니다. 이는 주로 시장의 급격한 변동에 민감하다는 데 나타납니다. 또한, 매개 변수 선택 및 필터링 조건은 복잡한 변동 시장에서 더 강한 적응력과 수익성을 얻기 위해 추가 테스트 및 최적화가 필요합니다.