왜 전통적인 기술 분석이 복잡한 시장에서 실패하는가?
양적 거래 분야에서 우리는 종종 이런 혼란을 겪습니다. 왜 간단한 이동 평균 또는 RSI에 기반한 전략이 특정 시장 환경에서 우수한 성과를 거두지만 다른 기간에는 자주 실패합니까? 그 대답은 금융 시간 순서의 복잡성에 있습니다. 그들은 자기 연관성이있을뿐만 아니라 시간에 따라 변동하는 변동률 특성이 있습니다.
오늘 분석하는 이 전략은 AR(2) 자기 회귀 모델과 GARCH(1,1) 조건부 차차 모델을 교묘하게 결합하여 이 문제를 통계학적인 관점에서 해결하려고 시도한다. 이것은 단순한 기술적 지표의 중첩이 아니라 금융 시퀀스의 본질적인 특성에 대한 깊은 탐구이다.
AR2) 모델은 가격의 기억 효과를 어떻게 포착하는가?
전략의 핵심은 AR(2) 자기 회귀 모델의 적용에 있다. 자기 회귀란 무엇인가? 간단히 말해서, 과거의 자기를 사용하여 미래의 자기를 예측하는 것이다. AR(2) 모델은 현재의 수익률을 앞 두 번의 수익률으로 선형적으로 나타낼 수 있다고 가정한다:
r_t = φ₁ × r_{t-1} + φ₂ × r_{t-2} + ε_t
코드에서 유레-워커 방정식을 통해 계수 φ1과 φ2를 풀기:
c0 = calcAutoCovariance(returns, 0, lengthReg) // 滞后0期自协方差
c1 = calcAutoCovariance(returns, 1, lengthReg) // 滞后1期自协方差
c2 = calcAutoCovariance(returns, 2, lengthReg) // 滞后2期自协方差
phi1 = (c1 * c0 - c2 * c1) / denominator // 第一个自回归系数
phi2 = (c2 * c0 - c1 * c1) / denominator // 第二个自回归系数
이 방법의 장점은 주관적인 판단에 의존하지 않고, 데이터 자체로 “말하게”하고, 가격 순서에 내재된 규칙성을 발견하는 것입니다.
왜 GARCH 모델이 시장의 위험을 더 잘 나타낼 수 있을까요?
AR 모델만으로는 충분하지 않습니다. 왜냐하면 금융 시장의 변동률은 일정하지 않기 때문입니다. 우리는 모두 ‘변동률 집합’ 현상이 큰 변동과 함께 큰 변동과 함께 큰 변동이있는 것을 알고 있습니다. 평온은 더 오래 지속됩니다.
GARCH(1,1) 모델은 바로 이런 특징을 묘사하기 위한 것입니다:
σ²_t = ω + α × ε²_{t-1} + β × σ²_{t-1}
코드의 구현 논리는 이것을 명확하게 나타냅니다:
omega = (1 - adjustedAlpha - adjustedBeta) * longTermVar
garchVariance := omega + adjustedAlpha * math.pow(arResidual[1], 2) + adjustedBeta * garchVariance[1]
여기서 중요한 통찰력은: 현재의 조건부 차이는 전기의 잔여차량 제곱 ((단기 충격) 에 의존하는 것뿐만 아니라 전기의 조건부 차이는 ((장기 지속성)) 에 의존한다. 변수 α는 단기 충격의 영향을 제어하고, β는 변동률의 지속성을 제어한다.
이 전략의 거래 논리는 어떻게 위험과 이익의 균형을 이룰 수 있을까요?
AR 예측과 GARCH 변동률 추정으로, 전략은 동적인 신뢰 간격을 구성한다:
upperReturnBand = arReturnPredict + stdevFactor * garchStd
lowerReturnBand = arReturnPredict - stdevFactor * garchStd
거래 신호의 생성 논리는 평균값 회귀의 생각을 반영한다:
- 가격이 하락할 때 더 많은 것을 할 수 있습니다
- 가격이 상반도를 돌파할 때 공백을 둡니다.
이 디자인의 교묘함은: 신뢰 영역의 폭은 시장의 변동률에 따라 동적으로 조정됩니다. 높은 변동 기간 동안, 영역은 넓어지고 거래 빈도가 감소합니다. 낮은 변동 기간 동안, 영역은 좁아지고 거래 기회가 증가합니다.
실제 적용에서 주의해야 할 중요한 문제들은 무엇입니까?
1. 모델 안정성 검사 코드는 중요한 안정성 검사를 포함합니다:
if stabilityCheck >= 0.99 or math.abs(phi2) >= 0.99
scaleFactor = 0.95 / math.max(stabilityCheck, math.abs(phi2) + 0.01)
이것은 AR 모델의 평형성을 보장하고 산란한 예측 결과를 방지한다.
2. 매개 변수 수렴성 제한 GARCH 모형은 α + β < 1을 요구하여 장기 차이의 존재를 보장한다:
if sumParam >= 0.999
scale = 0.99 / sumParam
3. 필터링 장치의 필요성 전략은 RSI 필터링 옵션을 제공하며 실제 응용에서 중요합니다. 순수 통계 모델은 시장의 추세적 특성을 무시 할 수 있으며, 기술 지표의 추가는 추가 확인 신호를 제공 할 수 있습니다.
전략의 한계와 개선방향
이 전략은 이론적으로는 우아하지만, 실제 적용에서는 다음과 같은 문제들을 고려해야 합니다.
데이터 주파수 선택:AR-GARCH 모델은 다른 주기 아래의 성능에 큰 차이가 있다. 높은 주파수 데이터는 더 많은 정보를 제공하지만 더 많은 소음을 도입한다.
매개 변수의 시간 변동성: 현재 구현 가정 AR 및 GARCH 매개 변수는 추정 창 내에서 일정하지만 실제 시장 구조는 변경될 수 있다.
거래 비용의 영향통계적 중매 전략은 일반적으로 높은 거래 횟수를 요구하며, 수수료와 슬라이드 포인트 비용은 무시할 수 없습니다.
결론: 통계 모델링의 가치와 양적 거래
이 AR-GARCH 전략은 금융 모델링에서 현대 통계학의 강력한 힘을 보여준다. 그것은 단순한 기술 지표 집합이 아니라 금융 시간 연속 통계 특성을 깊이 파고들었다.
양자 거래자들에게 이러한 전략들을 이해하는 가치는 직접적으로 적용하는 것 뿐만 아니라, 통계적 사고를 통해 시장을 분석하는 능력을 키우는 데 있습니다. AI와 기계 학습이 널리 퍼져있는 오늘날에도 이러한 고전적인 통계적 모델은 우리가 시장을 이해하고 전략을 세우는 데 중요한 기둥입니다.
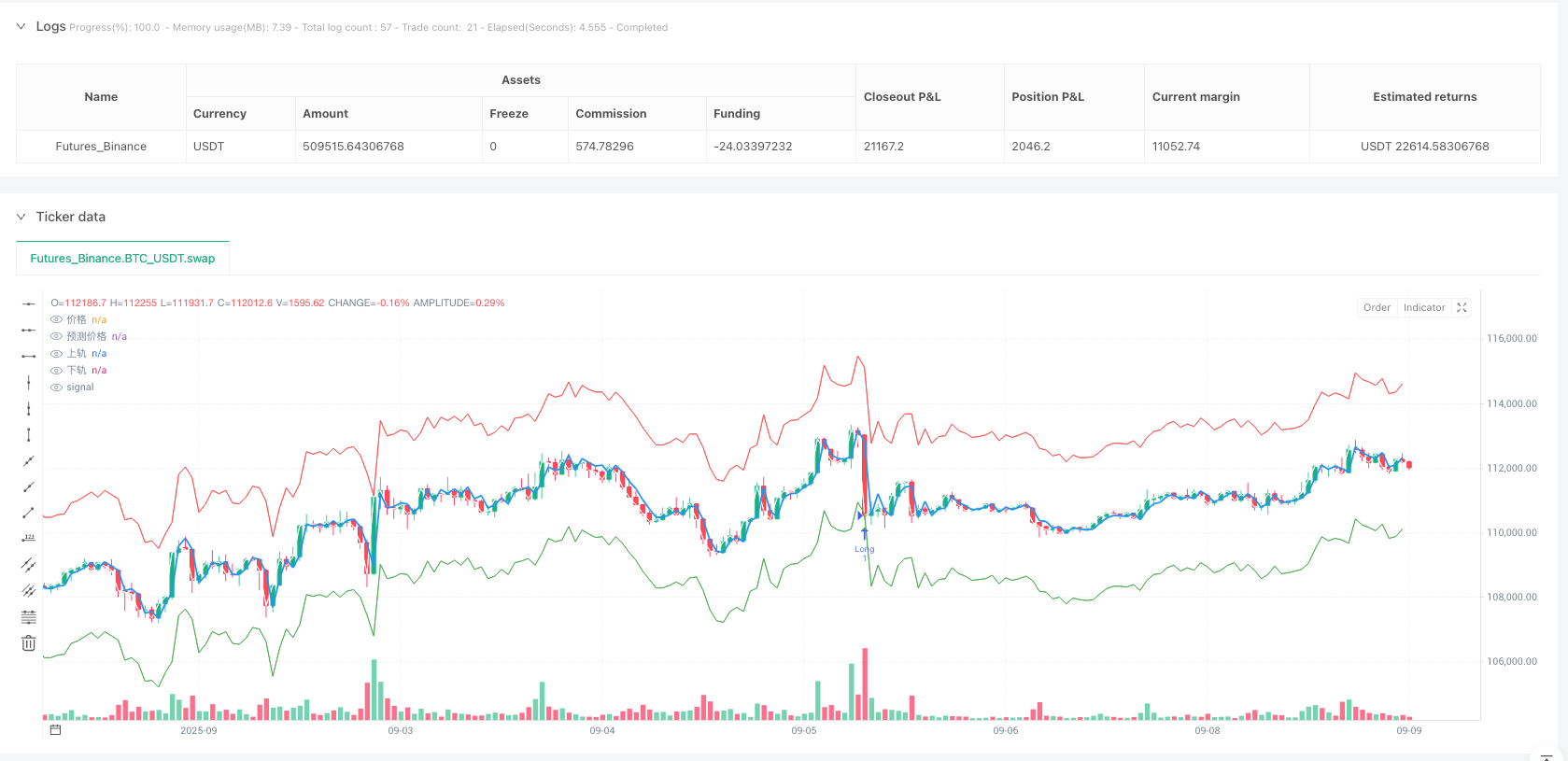
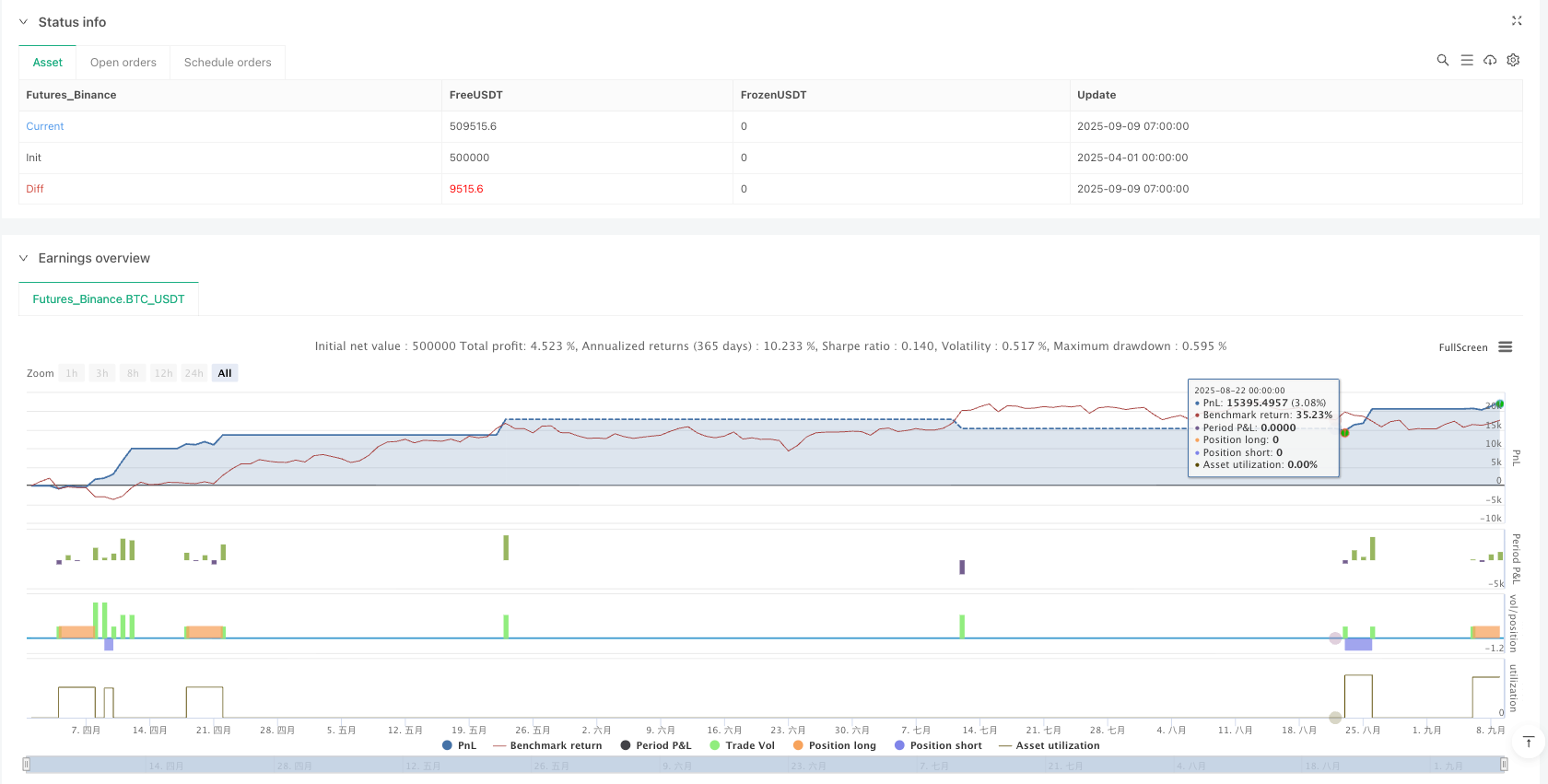
/*backtest
start: 2025-04-01 00:00:00
end: 2025-09-09 08:00:00
period: 1h
basePeriod: 1h
exchanges: [{"eid":"Futures_Binance","currency":"BTC_USDT","balance":500000}]
*/
//@version=5
strategy("AR(2)-GARCH Strategy", overlay=true)
//策略参数设置:配置AR模型、GARCH模型和交易信号的各项参数
lengthReg = input.int(50, "AR估计窗口", minval=50, maxval=200);//AR模型回归窗口长度
//GARCH波动率模型参数:控制条件方差的计算
useGarch = input.bool(true, "启用GARCH波动率");//是否启用GARCH波动率建模
garchAlpha = input.float(0.1, "GARCH Alpha", minval=0.01, maxval=0.3, step=0.01);//GARCH模型alpha参数
garchBeta = input.float(0.85, "GARCH Beta", minval=0.5, maxval=0.95, step=0.01);//GARCH模型beta参数
//交易信号生成参数:控制买卖信号的敏感度
stdevFactor = input.float(2.0, "标准差倍数", minval=1.0, maxval=3.0, step=0.1);//交易波段的标准差倍数
//风险控制参数:设置止损止盈水平
stopLossPerc = input.float(2.0, "止损 (%)", minval=0.5, maxval=5.0, step=0.1);//止损百分比
takeProfitPerc = input.float(4.0, "止盈 (%)", minval=1.0, maxval=10.0, step=0.1);//止盈百分比
//RSI过滤器参数:添加技术指标过滤条件
useRsiFilter = input.bool(false, "启用RSI过滤");//是否启用RSI过滤器
rsiLen = input.int(14, "RSI周期", minval=7, maxval=21);//RSI指标计算周期
rsiOB = input.float(70, "RSI超买线", minval=60, maxval=80);//RSI超买阈值
rsiOS = input.float(30, "RSI超卖线", minval=20, maxval=40);//RSI超卖阈值
//数据预处理:计算收益率序列
rawPrice = close;//原始收盘价
returns = math.log(rawPrice / rawPrice[1]);//对数收益率序列
//获取滞后收益率数据:AR(2)模型需要前两期的收益率数据
returns1 = returns[1];//滞后1期的收益率
returns2 = returns[2];//滞后2期的收益率
//计算收益率序列的移动平均值:作为AR模型的均值项
returnsMean = ta.sma(returns, lengthReg);//收益率的简单移动平均
//AR(2)模型系数计算:使用Yule-Walker方程求解自回归系数
//自协方差函数计算:计算不同滞后期的自协方差
calcAutoCovariance(data, lag, length) =>
mean = ta.sma(data, length);//计算数据的均值
sum = 0.0;//协方差累计值
count = 0;//有效数据点计数
for i = lag to length - 1
if not na(data[i]) and not na(data[i-lag])
sum := sum + (data[i] - mean) * (data[i-lag] - mean);//计算协方差分子
count := count + 1;//累计有效数据点
count > 0 ? sum / count : 0.0;//返回协方差值
//计算AR(2)模型所需的自协方差:用于Yule-Walker方程
c0 = calcAutoCovariance(returns, 0, lengthReg);//滞后0期的自协方差(即方差)
c1 = calcAutoCovariance(returns, 1, lengthReg);//滞后1期的自协方差
c2 = calcAutoCovariance(returns, 2, lengthReg);//滞后2期的自协方差
//Yule-Walker方程求解:计算AR(2)模型的两个自回归系数
// φ₁ = (c₁c₀ - c₂c₁) / (c₀² - c₁²)
// φ₂ = (c₂c₀ - c₁²) / (c₀² - c₁²)
denominator = c0 * c0 - c1 * c1;//分母计算
phi1 = denominator != 0 ? (c1 * c0 - c2 * c1) / denominator : 0.0;//第一个自回归系数
phi2 = denominator != 0 ? (c2 * c0 - c1 * c1) / denominator : 0.0;//第二个自回归系数
//AR(2)稳定性检验:确保模型稳定性条件 |φ₁| + |φ₂| < 1 且 |φ₂| < 1
stabilityCheck = math.abs(phi1) + math.abs(phi2);//计算系数绝对值之和
if stabilityCheck >= 0.99 or math.abs(phi2) >= 0.99
scaleFactor = 0.95 / math.max(stabilityCheck, math.abs(phi2) + 0.01);//计算缩放因子
phi1 := phi1 * scaleFactor;//调整第一个系数
phi2 := phi2 * scaleFactor;//调整第二个系数
//AR(2)收益率预测:根据历史收益率和AR系数预测下一期收益率
arReturnPredict = returnsMean + phi1 * (returns1 - returnsMean) + phi2 * (returns2 - returnsMean);//AR(2)预测公式
//计算AR模型的预测残差:用于GARCH建模
arResidual = returns - arReturnPredict;//AR模型的预测残差
//GARCH(1,1)波动率建模:对AR残差进行条件方差建模
var float garchVariance = na;//GARCH方差变量
var float longTermVar = na;//长期方差变量
//长期方差初始化:使用历史残差计算初始方差值
if na(longTermVar) and bar_index > lengthReg
longTermVar := ta.variance(arResidual, lengthReg);//计算长期方差
//GARCH参数调整:确保参数满足收敛条件
adjustedAlpha = garchAlpha;//调整后的alpha参数
adjustedBeta = garchBeta;//调整后的beta参数
sumParam = garchAlpha + garchBeta;//参数和
if sumParam >= 0.999
scale = 0.99 / sumParam;//计算参数缩放比例
adjustedAlpha := garchAlpha * scale;//调整alpha参数
adjustedBeta := garchBeta * scale;//调整beta参数
//GARCH(1,1)递归更新:根据GARCH公式更新条件方差
if useGarch and not na(longTermVar) and not na(arResidual)
if na(garchVariance)
garchVariance := longTermVar;//初始化GARCH方差
else
omega = (1 - adjustedAlpha - adjustedBeta) * longTermVar;//GARCH常数项
garchVariance := omega + adjustedAlpha * math.pow(arResidual[1], 2) + adjustedBeta * garchVariance[1];//GARCH递归公式
//条件标准差计算:从条件方差计算标准差
garchStd = useGarch and not na(garchVariance) ? math.sqrt(math.max(garchVariance, 0.0001)) : ta.stdev(arResidual, 20);//启用GARCH时使用条件标准差,否则使用历史标准差
//收益率空间的置信区间构建:基于AR预测和GARCH波动率
upperReturnBand = arReturnPredict + stdevFactor * garchStd;//上轨:预测收益率加上标准差倍数
lowerReturnBand = arReturnPredict - stdevFactor * garchStd;//下轨:预测收益率减去标准差倍数
//将置信区间转换为价格空间:用于实际交易信号生成
//基于预测收益率计算预测价格
predictedPrice = rawPrice[1] * math.exp(arReturnPredict);//根据预测收益率计算预测价格
upperPriceBand = rawPrice[1] * math.exp(upperReturnBand);//上轨价格
lowerPriceBand = rawPrice[1] * math.exp(lowerReturnBand);//下轨价格
//交易信号生成:基于当前价格相对于置信区间的位置
longSignal = rawPrice < lowerPriceBand;//做多信号:当前价格低于下轨
shortSignal = rawPrice > upperPriceBand;//做空信号:当前价格高于上轨
//RSI过滤器:使用RSI指标过滤交易信号
if useRsiFilter
rsi = ta.rsi(rawPrice, rsiLen);//计算RSI指标
longSignal := longSignal and rsi < rsiOS;//做多信号需要RSI超卖确认
shortSignal := shortSignal and rsi > rsiOB;//做空信号需要RSI超买确认
//策略执行:根据交易信号开仓和平仓
//开仓操作:根据信号建立多头或空头仓位
if longSignal
strategy.entry("Long", strategy.long);//开多仓
if shortSignal
strategy.entry("Short", strategy.short);//开空仓
//风险控制:设置止损止盈条件
if strategy.position_size > 0
strategy.exit("Long Exit", "Long",
stop=strategy.position_avg_price * (1 - stopLossPerc/100),
limit=strategy.position_avg_price * (1 + takeProfitPerc/100));//多仓止损止盈
if strategy.position_size < 0
strategy.exit("Short Exit", "Short",
stop=strategy.position_avg_price * (1 + stopLossPerc/100),
limit=strategy.position_avg_price * (1 - takeProfitPerc/100));//空仓止损止盈
//图表显示:在图表上绘制价格、预测线和交易信号
//主要价格线和预测线:显示实际价格和基于收益率预测的价格
plot(rawPrice, color=color.white, linewidth=1, title="价格");//绘制实际价格线
plot(predictedPrice, color=color.blue, linewidth=2, title="预测价格");//绘制预测价格线
plot(upperPriceBand, color=color.red, linewidth=1, title="上轨");//绘制上轨线
plot(lowerPriceBand, color=color.green, linewidth=1, title="下轨");//绘制下轨线
//交易信号标记:在图表上标记买卖信号点
plotshape(longSignal, style=shape.triangleup, location=location.belowbar,
color=color.green, size=size.small, title="买入");//标记买入信号
plotshape(shortSignal, style=shape.triangledown, location=location.abovebar,
color=color.red, size=size.small, title="卖出");//标记卖出信号